2-Hop Eclipse: A Fast Algorithm for Bandwidth-Efficient Data Center Switching

Abstract

A hybrid-switched data center network interconnects its racks of servers with a combination of a fast circuit switch that a schedule can reconfigure at significant cost and a much slower packet switch that a schedule can reconfigure at negligible cost. Given a traffic demand matrix between the racks, how can we best compute a good circuit switch configuration schedule that meets most of the traffic demand, leaving as little as possible for the packet switch to handle?

In this paper we propose 2-hop Eclipse, a new hybrid switch scheduling algorithm that strikes a much better tradeoff between the performance of the hybrid switch and the computational complexity of the algorithm, both in theory and in simulations, than the current state of the art solution Eclipse/Eclipse++.

1 Introduction

Fueled by the phenomenal growth of cloud computing services, data center networks (DCN) continue to grow relentlessly both in size, as measured by the number of racks of servers it has to interconnect, and in speed, as measured by the amount of traffic it has to transport per unit of time from/to each rack [1]. A traditional data center network architecture typically consists of a three-level multi-rooted tree of switches that start, at the lowest level, with the Top-of-Rack (ToR) switches, that each connects a rack of servers to the network [2]. However, such an architecture has become increasingly unable to scale with the explosive growth in both the size and the speed of the DCN, as we can no longer increase the transporting and switching capabilities of the underlying commodity packet switches without increasing their costs significantly.

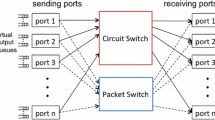
A cost-effective solution approach to this scalability problem, called hybrid circuit and packet switching, has received considerable research attention in recent years [3,4,5]. In a hybrid-switched DCN, shown in Fig. 1, n racks of computers on the left hand side (LHS) are connected by both a circuit switch and a packet switch to n racks on the right hand side (RHS). Note that racks on the LHS are an identical copy of those on the RHS; however we restrict the role of the former to only transmitting data and refer to them as input ports, and restrict the role of the latter to only receiving data and refer to them as output ports. The purpose of this duplication (of racks) and role restrictions is that the resulting hybrid data center topology can be modeled as a bipartite graph.

Fig. 1.

Hybrid circuit and packet switch

Each switch transmits data from input ports (racks on the LHS) to output ports (racks on the RHS) according to the configuration (modeled as a bipartite matching) of the switch at the moment. Usually, the circuit switch is an optical switch [3, 6, 7], and the packet switch is an electronic switch. Hence the circuit switch is typically an order of magnitude or more faster than the packet switch. For example, the circuit and packet switches might operate at the respective rates of 100 Gbps and 10 Gbps per port. The flip side of the coin however is that the circuit switch incurs a nontrivial reconfiguration delay $\delta$ when its configuration has to change. Depending on the underlying technology of the circuit switch, $\delta$ can range from tens of microseconds to tens of milliseconds [3, 6,7,8,9].

In this paper, we study an important optimization problem stemming from hybrid circuit and packet switching: Given a traffic demand matrix D from input ports to output ports, how to schedule the circuit switch to best (e.g., in the shortest amount of total transmission time) meet the demand? A schedule for the circuit switch consists of a sequence of configurations (matchings) and their time durations $(M_1, \alpha _1), (M_2, \alpha _2), \cdots , (M_K, \alpha _K)$. A workable schedule should let the circuit switch remove (i.e., transmit) most of the traffic demand from D, so that every row or column sum of the remaining traffic matrix is small enough for the packet switch to handle. Since the problem of computing the optimal schedule for hybrid switching, in various forms, is NP-hard [10], almost all existing solutions are greedy heuristics.

1.1 State of the Art: Eclipse and Eclipse++

Since our solution builds upon the state of the art solution called Eclipse [11], we provide here a brief description of it, and its companion algorithm Eclipse++ [11]. Eclipse iteratively chooses a sequence of circuit switch configurations, one per iteration, according to the following greedy criteria: In each iteration, Eclipse tries to extract and subtract a matching (with its duration) from the $n\times n$ traffic demand matrix D that has the largest cost-adjusted utility, which we will specify precisely in Sect. 3. Eclipse, like most other hybrid switching algorithms, considers and allows only direct routing in the following sense: All circuit-switched data packets reach their respective final destinations in one-hop (i.e., enters and exits the circuit switch only once).

However, restricting the solution strategy space to only direct routing algorithms may leave the circuit switch underutilized. For example, a connection (edge) from input $i_0$ to output $j_0$ belongs to a matching M that lasts 50 $\upmu$s, but at the start time of this matching, there is only 40 $\upmu$s worth of traffic left for transmission from $i_0$ to $j_0$, leaving 10 $\upmu$s of “slack” (i.e., residue capacity) along this connection. The existence of connections (edges) with such “slacks” makes it possible to perform indirect (i.e., multi-hop) routing of remaining traffic via one or more relay nodes through a path consisting of such edges.

Besides Albedo [12], Eclipse++ [11] is the only other work that has explored indirect routing in hybrid switching. It was shown in [11] that optimal indirect routing using such “slacks”, left over by a direct routing solution such as Eclipse, can be formulated as the maximum multi-commodity flow over a “slack graph”, which is NP-complete [13,14,15,16]. Eclipse++ is a greedy heuristic that converts, with “precision loss” (otherwise P = NP), this multi-commodity flow computation to a large set of shortest-path computations. Hence the computational complexity of Eclipse++ is still extremely high: Both us and the authors of [11] found that Eclipse++ is roughly three orders of magnitude more computationally expensive than Eclipse [17] for a data center with $n = 100$ racks.

1.2 Our Solution

We develop a new problem formulation that allows the joint optimization of both direct and 2-hop indirect routing, at the same time, against the aforementioned cost-adjusted utility function. We obtain our solution, called 2-hop Eclipse, by applying the Eclipse algorithm as basis for a greedy heuristic to this new optimization problem. This 2-hop Eclipse algorithm, a slight yet subtle modification of Eclipse, has the same asymptotic computational complexity and comparable execution time as Eclipse, but has higher performance gains over Eclipse than Eclipse++, despite the fact that Eclipse++ is three orders of magnitude more computationally expensive.

We emphasize that 2-hop Eclipse uses a very different strategy than Eclipse++ and in particular has no resemblance to “Eclipse++ restricted to 2-hops”, which according to our simulations performs slightly worse than, and has almost the same computational complexity as unrestricted Eclipse++.

The rest of the paper is organized as follows. In Sect. 2, we describe the system model and the design objective of this hybrid switch scheduling problem in details. In Sect. 3, we provides a more detailed description of Eclipse [11]. In Sect. 4, we present our solution, 2-hop Eclipse. In Sect. 5, we evaluate the performance of our solution against Eclipse and Eclipse++. Finally, we describe related work in Sect. 6 and conclude the paper in Sect. 7.

2 System Model and Problem Statement

In this section, we formulate the problem of hybrid circuit and packet switching precisely. We first specify the aforementioned traffic demand traffic D precisely. Borrowing the term virtual output queue (VOQ) from the crossbar switching literature [18], we refer to, the set of packets that arrive at input port i and are destined for output j, as VOQ(i, j). The demand matrix entry D(i, j) is the amount of VOQ(i, j) traffic, within a scheduling window, that needs to be scheduled for transmission by the hybrid switch. It was effectively assumed, in all prior works on hybrid switching except Albedo [12] (to be discussed in Sect. 6.1), that the demand matrix D is precisely known before the computation of the circuit switch schedule begins (say at time t). Consequently, all prior hybrid switching algorithms except Albedo [12] perform only batch scheduling of this D. In other words, given a demand matrix D, the schedules of the circuit and the packet switches are computed before the transmissions of the batch (i.e., traffic in D) actually happen. Our 2-hop Eclipse algorithm also assumes that D is precisely known in advance and is designed for batch scheduling only. Since batch scheduling is offline in nature (i.e., requires no irrevocable online decision-making), 2-hop Eclipse algorithm is allowed to “travel back in time” and modify the schedules of the packet and the circuit switches as needed.

In this work, we study this problem of hybrid switch scheduling under the following standard formulation that was introduced in [19]: to minimize the amount of time for the circuit and the packet switches working together to transmit a given traffic demand matrix D. We refer to this amount of time as transmission time throughout this paper. A schedule of the circuit switch consists of a sequence of circuit switch configurations and their durations: $(M_1, \alpha _1), (M_2, \alpha _2), \cdots , (M_K, \alpha _K)$. Each $M_k$ is an $n\times n$ permutation (matching) matrix; $M_k(i,j) = 1$ if input i is connected to output j and $M_k(i,j) = 0$ otherwise. The total transmission time of the above schedule is $K \delta +\sum _{k=1}^K \alpha _k$, where $\delta$ is the reconfiguration delay, K is the total number of configurations in the schedule.

Since computing the optimal circuit switch schedule alone (i.e., when there is no packet switch), in its full generality, is NP-hard [10], almost all existing solutions are greedy heuristics. Indeed, the typical workloads we see in data centers exhibit two characteristics that are favorable to such greedy heuristics: sparsity (the vast majority of the demand matrix elements have value 0 or close to 0) and skewness (few large elements in a row or column account for the majority of the row or column sum) [19].

3 Background on Eclipse

Since our 2-hop Eclipse algorithm builds upon Eclipse [11], we provide here a more detailed description of Eclipse. Eclipse iteratively chooses a sequence of configurations, one per iteration, according to the following greedy criteria: In each iteration, Eclipse tries to extract and subtract a matching from the demand matrix D that has the largest cost-adjusted utility, defined as follows. For a configuration $(M,\alpha )$ (using a permutation matrix M for a duration of $\alpha$), its utility $U(M,\alpha )$, before adjusting for cost, is $U(M,\alpha ) \triangleq \Vert \min (\alpha M,D_{\text {rem}})\Vert _1$, where $D_{\text {rem}}$ denotes what remains of the traffic demand (matrix) D after we subtract from it the amounts of traffic to be served by the circuit switch according to the previous matchings, i.e., those computed in the previous iterations. Note that $U(M,\alpha )$ is precisely the total amount of traffic the configuration $(M,\alpha )$ would remove from D. The cost of the configuration $(M,\alpha )$ is modeled as $\delta + \alpha$, which accounts for the reconfiguration delay $\delta$. The cost-adjusted utility is simply their quotient $\frac{U(M,\alpha )}{\delta + \alpha }$. Although the problem of maximizing this cost-adjusted utility is very computationally expensive, it was shown in [11] that an computationally efficient heuristic algorithm solution exists that empirically produces the optimal value most of time. This solution, invoking the scaling algorithm for computing maximum weighted matching (MWM) [20] $O(\log n)$ times, has a (relatively) low computational complexity of $O(n^{5/2}\log n\log B)$, where B is the value of the largest element in D. Hence the computational complexity of Eclipse is $O(Kn^{5/2}\log n\log B)$, shown in Table 1, where K is the total number of matchings (iterations) used.

Table 1. Comparison of time complexities

4 Design of 2-Hop Eclipse

Unlike Eclipse, which considers only direct routing, 2-hop Eclipse considers both direct routing and 2-hop indirect routing in its optimization. More specifically, 2-hop Eclipse iteratively chooses a sequence of configurations that maximizes the cost-adjusted utility, just like Eclipse, but the cost-unadjusted utility $U(M, \alpha )$ here accounts for not only the traffic that can be transmitted under direct routing, but also that can be indirectly routed over all possible 2-hop paths.

We make a qualified analogy between this scheduling of the circuit switch and the scheduling of “flights”. We view the connections (between the input ports and the output ports) in a matching $M_k$ as “disjoint flights” (those that share neither a source nor a destination “airport”) and the residue capacity on such a connection as “available seats”. We view Eclipse, Eclipse++, and 2-hop Eclipse as different “flight booking” algorithms. Eclipse books “passengers” (traffic in the demand matrix) for “non-stop flights” only. Then Eclipse++ books the “remaining passengers” for “flights with stops” using only the “available seats” left over after Eclipse does its “bookings”. Different than Eclipse++, 2-hop Eclipse “books passengers” for both “non-stop” and “one-stop flights” early on, although it does try to put “passengers” on “non-stop flights” as much as possible, since each “passenger” on a “one-stop flight” costs twice as many “total seats” as that on a “non-stop flight”.

It will become clear shortly that the sole purpose of this qualified analogy is for us to distinguish two types of “passengers” in presenting the 2-hop Eclipse algorithm: those “looking for a non-stop flight” whose counts are encoded as the remaining demand matrix $D_{\text {rem}}$, and those “looking for a connection flight” to complete their potential “one-stop itineraries”, whose counts are encoded as a new $n\times n$ matrix $I_{\text {rem}}$ that we will describe shortly. We emphasize that this analogy shall not be stretched any further, since it would otherwise lead to absurd inferences, such as that such a set of disjoint “flights” must span the same time duration and have the same number of “seats” on them.

4.1 The Pseudocode

The pseudocode of 2-hop Eclipse is shown in Algorithm 1. It is almost identical to that of Eclipse [11]. The only major difference is that in each iteration (of the “while” loop), 2-hop Eclipse searches for a matching $(M, \alpha )$ that maximizes $\frac{\Vert \min (\alpha M,\,D_{\text {rem}}+I_{ \text {rem}})\Vert _1}{\delta +\alpha }$, whereas Eclipse searches for one that maximizes $\frac{\Vert \min (\alpha M,\,D_{ \text {rem}})\Vert _1}{\delta +\alpha }$. In other words, in each iteration, 2-hop Eclipse first performs some preprocessing to obtain $I_{ \text {rem}}$ and then substitute the parameter $D_{ \text {rem}}$ by $D_{ \text {rem}} + I_{ \text {rem}}$ in making the “argmax” call (Line 7). The “while” loop of Algorithm 1 terminates when every row or column sum of $D_{ \text {rem}}$ is no more than $r_p t_c$, where $r_p$ denotes the (per-port) transmission rate of the packet switch and $t_c$ denotes the total transmission time used so far by the circuit switch, since the remaining traffic demand can be transmitted by the packet switch (in $t_c$ time). Note there is no occurrence of $r_c$, the (per-port) transmission rate of the circuit switch, in Algorithm 1, because we normalize $r_c$ to 1 throughout this paper.

4.2 The Matrix $I_{\text {rem}}$

Just like $D_{ \text {rem}}$, the value of $I_{ \text {rem}}$ changes after each iteration. We now explain the value of $I_{ \text {rem}}$, at the beginning of the $k^{th}$ iteration ($k > 1$). To do so, we need to first introduce another matrix R. As explained earlier, among the edges that belong to the matchings $(M_1, \alpha _1), (M_2, \alpha _2), \cdots , (M_{k-1}, \alpha _{k-1})$ computed in the previous $k-1$ iterations, some may have residue capacities. These residue capacities are captured in an $n\times n$ matrix R as follows: R(l, i) is the total residue capacity of all edges from input l to output i that belong to one of these (previous) $k-1$ matchings. Under the qualified analogy above, R(l, i) is the total number of “available seats on all previous flights from airport l to airport i”. We refer to R as the (cumulative) residue capacity matrix in the sequel.

Now we are ready to define $I_{ \text {rem}}$. Consider that, at the beginning of the $k^{th}$ iteration, $D_{ \text {rem}}(l,j)$ “local passengers” (i.e., those who are originated at l) who need to fly to j remain to have their “flights” booked. Under Eclipse, they have to be booked on either a “non-stop flight” or a “bus” (i.e., through the packet switch) to j. Under 2-hop Eclipse, however, there is a third option: a “one-stop flight” through an intermediate “airport”. 2-hop Eclipse explores this option as follows. For each possible intermediate “airport” i such that $R(l, i) > 0$ (i.e., there are “available seats” on one or more earlier “flights” from l to i), $I^{(l)}_{ \text {rem}}(i,j)$ “passengers” will be on the “speculative standby list” at “airport” i, where

$$\begin{aligned} I^{(l)}_{ \text {rem}}(i,j)\triangleq \min \big (D_{ \text {rem}}(l,j),R(l,i)\big ). \end{aligned}$$

(1)

In other words, up to $I^{(l)}_{ \text {rem}}(i,j)$ “passengers” could be booked on “earlier flights” from l to i that have R(l, i) “available seats”, and “speculatively stand by” for a “flight” from i to j that might materialize as a part of matching $M_k$.

The matrix element $I_{ \text {rem}}(i,j)$ is the total number of “nonlocal passengers” who are originated at all “airports” other than i and j and are on the “speculative standby list” for a possible “flight” from i to j. In other words, we have

$$\begin{aligned} I_{ \text {rem}}(i,j)\triangleq \sum _{l\in [n]\setminus \{i,j\}}I^{(l)}_{ \text {rem}}(i,j). \end{aligned}$$

(2)

Recall that $D_{ \text {rem}}(i,j)$ is the number of “local passengers” (at i) that need to travel to j. Hence at the “airport” i, a total of $D_{ \text {rem}}(i,j) + I_{ \text {rem}}(i,j)$ “passengers”, “local or nonlocal”, could use a “flight” from i to j (if it materializes in $M_k$). We are now ready to precisely state the difference between Eclipse and 2-hop Eclipse: Whereas $\Vert \min (\alpha M, D_{ \text {rem}})\Vert _1$, the cost-unadjusted utility function used by Eclipse, accounts only for “local passengers”, $\Vert \min (\alpha M, D_{ \text {rem}}+I_{ \text {rem}})\Vert _1$, that used by 2-hop Eclipse, accounts for both “local” and “nonlocal passengers”.

Note that the term $D_{ \text {rem}}(l,j)$ appears in the definition of $I^{(l)}_{ \text {rem}}(i,j)$ (Formula (1)), for all $i\in [n]\setminus \{l,j\}$. In other words, “passengers” originated at l who need to travel to j could be on the “speculative standby list” at multiple intermediate “airports”. This is however not a problem (i.e., will not result in “duplicate bookings”) because at most one of these “flights” (to j) can materialize as a part of matching $M_k$.

4.3 Update $D_{\text {rem}}$ and R

After the schedule $(M_k, \alpha _k)$ is determined by the “argmax call” (Line 7 in Algorithm 1) in the $k^{th}$ iteration, the action should be taken on “booking” the right set of “passengers” on the “flights” in $M_k$, and updating $D_{ \text {rem}}$ (Line 10) and R (Line 11) accordingly. Recall that we normalize $r_c$, the service rate of the circuit switch, to 1, so all these flights have $\alpha _k \times 1 = \alpha _k$ “available seats”. We only describe how to do so for a single “flight” (say from i to j) in $M_k$; that for other “flights” in $M_k$ is similar. Recall that $D_{ \text {rem}}(i,j)$ “local passengers” and $I_{ \text {rem}}(i,j)$ “nonlocal passengers” are eligible for a “seat” on this “flight”. When there are not enough seats for all of them, 2-hop Eclipse prioritizes “local passengers” over “nonlocal passengers”, because the former is more resource-efficient to serve than the latter, as explained earlier. There are three possible cases:

• (I) $\alpha \le D_{ \text {rem}}(i,j)$. In this case, only a subset of “local passengers” (directly routed traffic), in the “amount” of $\alpha _k$, are booked on this “flight”, and $D_{ \text {rem}}(i,j)$ is hence decreased by $\alpha$. There is no “available seat” on this “flight” so the value of R(i, j) is unchanged.

• (II) $\alpha \ge D_{ \text {rem}}(i,j)+I_{ \text {rem}}(i,j)$. In this case, all “local” and “nonlocal passengers” are booked on this “flight”. After all these “bookings”, $D_{ \text {rem}}(i,j)$ is set to 0 (all “local passengers” traveling to j gone), and for each $l\in [n]\setminus \{i,j\}$, $D_{ \text {rem}}(l,j)$ and R(l, i) each is decreased by $I^{(l)}_{ \text {rem}}(i,j)$ to account for the resources consumed by the indirect routing of traffic demand (i.e., “nonlocal passengers”), in the amount of $I^{(l)}_{ \text {rem}}(i,j)$, from l to j via i. Finally, R(i, j) is increased by $\alpha -\big (D_{ \text {rem}}(i,j)+I_{ \text {rem}}(i,j)\big )$, the number of “available seats” that remain on this flight after all these “bookings”.

• (III) $D_{ \text {rem}}(i,j)<\alpha <D_{ \text {rem}}(i,j)+I_{ \text {rem}}(i,j)$. In this case, all “local passengers” are booked on this “flight”, so $D_{ \text {rem}}(i,j)$ is set to 0. However, different from the previous case, there are not enough “available seats” left on this “flight” to accommodate all $I_{ \text {rem}}(i,j)$ “nonlocal passengers”, so only a proper “subset” of them can be booked on this “flight”. We allocate this proper “subset” proportionally to all origins $l\in [n]\setminus \{i,j\}$. More specifically, for each $l\in [n]\setminus \{i,j\}$, we book $\theta \cdot I^{(l)}_{ \text {rem}}(i,j)$ “nonlocal passengers” originated at l on one or more “earlier flights” from l to i, and also on this “flight”, where $\theta \triangleq \frac{\alpha -D_{ \text {rem}(i,j)}}{I_{ \text {rem}}(i,j)}$. Similar to that in the previous case, after these “bookings”, $D_{ \text {rem}}(l,j)$ and R(l, i) each is decreased by $\theta \cdot I^{(l)}_{ \text {rem}}(i,j)$. Finally, R(i, j) is unchanged as this “flight” is full.

We restrict indirect routing to most 2 hops in 2-hop Eclipse because the aforementioned “duplicate bookings” could happen if indirect routing of 3 or more hops are allowed, making its computation not “embeddable” into the Eclipse algorithm and hence much more computationally expensive. This restriction is however by no means punitive: 2-hop indirect routing appears to have reaped most of the performance benefits from indirect routing, as shown in Sect. 5.5.

4.4 Complexities of 2-Hop Eclipse

Each iteration in 2-hop Eclipse has only a slightly higher computational complexity than that in Eclipse. This additional complexity comes from Lines 6, 10, and 11 in Algorithm 1. We need only to analyze the complexity of Line 6 (for updating $I^{(l)}_{ \text {rem}}$), since it dominates those of others. For each k, the complexity of Line 6 in the $k^{th}$ iteration is $O(kn^2)$ because there were at most $(k-1)n$ “flights” in the past $k-1$ iterations, and for each such flight (say from l to i), we need to update at most $n-2$ variables, namely $I^{(l)}_{ \text {rem}}(i,j)$ for all $j\in [n]\setminus \{l,i\}$. Hence the total additional complexity across all iterations is $O(\min (K,n)Kn^2)$, where K is the number of iterations actually executed by 2-hop Eclipse. Adding this to $O(n^{5/2}\log n\log B)$, the complexity of Eclipse, we arrive at the complexity of 2-hop Eclipse: $O(Kn^{5/2}\log n\log B+\min (K,n)Kn^2)$ (see Table 1). We found that the execution times of 2-hop Eclipse are only roughly $20\%$ to $40\%$ longer than that of Eclipse, for the instances (scheduling scenarios) used in our evaluations. Also shown in Table 1, the computational complexity of Eclipse++ is much higher than those of both Eclipse and 2-hop Eclipse. Here W denotes the maximum row/column sum of the demand matrix. Finally, it is not hard to check that the space (memory) complexity of 2-hop Eclipse is $O(\max (K,n)n)$, which is empirically only slightly larger than $O(n^2)$, that of Eclipse. This O(Kn) additional space is needed to store the residue capacities (of no more than n links in each schedule) induced by each schedule $(M_k,\alpha _k)$.

5 Evaluation

In this section, we evaluate the performance of 2-hop Eclipse and compare it with those of Eclipse and Eclipse++, under various system parameter settings and traffic demands. We do not however have Eclipse++ in all performance figures because its computational complexity is so high that it usually takes a few hours to compute a schedule. However, those Eclipse++ simulation results we managed to obtain and present in Sect. 5.5 show conclusively that the small reductions in transmission time using Eclipse++ are not worth its extremely high computational complexity. We do not compare our solutions with Solstice [19] (to be described in Sect. 6.1) in these evaluations, since Solstice was shown in [11] to perform worse than Eclipse in all simulation scenarios. For all these comparisons, we use the same performance metric as that used in [19]: the total time needed for the hybrid switch to transmit the traffic demand D.

5.1 Traffic Demand Matrix D

For our simulations, we use the same traffic demand matrix D as used in other hybrid scheduling works [11, 19]. In this matrix, each row (or column) contains $n_L$ large equal-valued elements (large input-output flows) that as a whole account for $c_L$ (percentage) of the total workload to the row (or column), $n_S$ medium equal-valued elements (medium input-output flows) that as a whole account for the rest $c_S = 1- c_L$ (percentage), and noises. Roughly speaking, we have

$$\begin{aligned} D=(\sum \limits _{i=1}^{n_L} \frac{c_L}{n_L}P_i+\sum \limits _{i=1}^{n_S} \frac{c_S}{n_S}P'_{i}+\mathcal {N}_1)\times 90\%+\mathcal {N}_2 \end{aligned}$$

(3)

where $P_i$ and $P'_{i}$ are random $n\times n$ matching (permutation) matrices.

The parameters $c_L$ and $c_S$ control the aforementioned skewness (few large elements in a row or column account for the majority of the row or column sum) of the traffic demand. Like in [11, 19], the default values of $c_L$ and $c_S$ are 0.7 (i.e., $70\%$) and 0.3 (i.e., $30\%$) respectively, and the default values of $n_L$ and $n_S$ are 4 and 12 respectively. In other words, in each row (or column) of the demand matrix, by default the 4 large flows account for $70\%$ of the total traffic in the row (or column), and the 12 medium flows account for the rest $30\%$. We will also study how these hybrid switching algorithms perform when the traffic demand has other degrees of skewness by varying $c_L$ and $c_S$.

Fig. 2.

Performance comparison under different system settings

As shown in Eq. (3), we also add two noise matrix terms $\mathcal {N}_1$ and $\mathcal {N}_2$ to D. Each nonzero element in $\mathcal {N}_1$ is a Gaussian random variable that is to be added to a traffic demand matrix element that was nonzero before the noises are added. This noise matrix $\mathcal {N}_1$ was also used in [11, 19]. However, each nonzero (noise) element here in $\mathcal {N}_1$ has a larger standard deviation, which is equal to 1 / 5 of the value of the demand matrix element it is to be added to, than that in [11, 19], which is equal to $0.3\%$ of 1 (the normalized workload an input port receives during a scheduling window, i.e., the sum of the corresponding row in D). We increase this additive noise here to highlight the performance robustness of our algorithm to such perturbations.

Different than in [11, 19], we also add (truncated) positive Gaussian noises $\mathcal {N}_2$ to a portion of the zero entries in the demand matrix in accordance with the following observation. Previous measurement studies have shown that “mice flows” in the demand matrix are heavy-tailed [21] in the sense the total traffic volume of these “mice flows” is not insignificant. To incorporate this heavy-tail behavior in the traffic demand matrix, we add such a positive Gaussian noise – with standard deviation equal to $0.3\%$ of 1 – to $50\%$ of the zero entries of the demand matrix. This way the “mice flows” collectively carry approximately $10\%$ of the total traffic volume. To bring the normalized workload back to 1, we scale the demand matrix by $90\%$ before adding $\mathcal {N}_2$, as shown in Eq. (3).

Fig. 3.

Performance comparison while varying sparsity of demand matrix

5.2 System Parameters

In this section, we introduce the system parameters (of the hybrid switch) used in our simulations.

Network Size: We consider the hybrid switch with $n=100$ input/output ports. Other reasonably large (say $\ge$32) switch sizes produce similar results.

Circuit Switch Per-Port Rate $r_c$ and Packet Switch Per-Port Rate $r_p$ : As far as designing hybrid switching algorithms is concerned, only their ratio $r_c/r_p$ matters. This ratio roughly corresponds to the percentage of traffic that needs to be transmitted by the circuit switch. The higher this ratio is, the higher percentage of traffic should be transmitted by the circuit switch. This ratio varies from 8 to 40 in our simulations. As explained earlier, we normalize $r_c$ to 1 throughout this paper. Since both the traffic demand to each input port and the per-port rate of the circuit switch are all normalized to 1, the (idealistic) transmission time would be 1 when there was no packet switch, the scheduling was perfect (i.e., no “slack” anywhere), and there was no reconfiguration penalty (i.e., $\delta = 0$). Hence we should expect that all these algorithms result in transmission times larger than 1 under realistic “operating conditions” and parameter settings.

Reconfiguration Delay (of the Circuit Switch) $\delta$ : In general, the smaller this reconfiguration delay is, the less time the circuit switch has to spend on reconfigurations. Hence, given a traffic demand matrix, the transmission time should increase as $\delta$ increases.

5.3 Performances Under Different System Parameters

In this section, we evaluate the performances of Eclipse and 2-hop Eclipse for different value combinations of $\delta$ and $r_c/r_p$ under the traffic demand matrix with the default parameter settings (4 large flows and 12 small flows accounting for roughly $70\%$ and $30\%$ of the total traffic demand into each input port). For each scenario, we perform 100 simulation runs, and report the average transmission time and the 95% confidence interval (the vertical error bar) in Fig. 2. As shown in Fig. 2, 2-hop Eclipse performs better than Eclipse, especially when reconfiguration delay $\delta$ and rate ratio $r_c/r_p$ are large. For example, when $\delta =0.01,r_c/r_p=10$ (default setting), the average transmission time under 2-hop Eclipse is approximately $13\%$ shorter than that under Eclipse, and when $\delta =0.04, r_c/r_p=20$, that under 2-hop Eclipse is $23\%$ shorter. The performance of 2-hop Eclipse is also less variable than Eclipse: In all these scenarios, the confidence intervals (of the transmission time) under 2-hop Eclipse are slightly smaller than that under Eclipse.

Fig. 4.

Performance comparison while varying skewness of demand matrix

5.4 Performances Under Different Traffic Demands

In this section, we evaluate the performance robustness of our algorithm 2-hop Eclipse under a large set of traffic demand matrices that vary by sparsity and skewness. We control the sparsity of the traffic demand matrix D by varying the total number of flows ($n_L+n_S$) in each row from 4 to 32, while fixing the ratio of the number of large flow to that of small flows ($n_L/n_S$) at 1 : 3. We control the skewness of D by varying $c_S$, the total percentage of traffic carried by small flows, from $5\%$ (most skewed as large flows carry the rest $95\%$) to $75\%$ (least skewed). In all these evaluations, we consider four different value combinations of system parameters $\delta$ and $r_c/r_p$: (1) $\delta =0.01, r_c/r_p=10$; (2) $\delta =0.01, r_c/r_p=20$; (3) $\delta =0.04, r_c/r_p=10$; and (4) $\delta =0.04, r_c/r_p=20$.

Figure 3 compares the transmission time of 2-hop Eclipse and Eclipse when the sparsity parameter $n_L+n_S$ varies from 4 to 32 and the value of the skewness parameter $c_S$ is fixed at 0.3. Figure 4 compares the transmission time of 2-hop Eclipse and Eclipse when the the skewness parameter $c_S$ varies from $5\%$ to $75\%$ and the sparsity parameter $n_L+n_S$ is fixed at 16 ($=4 + 12$). In each figure, the four subfigures correspond to the four value combinations of $\delta$ and $r_c/r_p$ above.

Both Figs. 3 and 4 show that 2-hop Eclipse performs better than Eclipse under various traffic demand matrices, especially when the traffic demand matrix becomes dense (as the number of flows $n_L+n_S$ increases in Fig. 4). This shows that 2-hop indirect routing can reduce transmission time significantly under a dense traffic demand matrix. This is not surprising: Dense matrix means smaller matrix elements, and it is more likely for a small matrix element to be transmitted entirely by indirect routing (in which case there is no need to pay a large reconfiguration delay for the direct routing of it) than for a large one.

Fig. 5.

Performance comparison of Eclipse, 2-hop Eclipse and Eclipse++

5.5 Compare 2-Hop Eclipse with Eclipse++

In this section, we compare the performances of 2-hop Eclipse and Eclipse++, both indirect routing algorithms, under the default parameter settings. Since Eclipse++ has a very high computational complexity, we perform only 50 simulation runs for each scenario. The results are shown in Fig. 5. They show that Eclipse++ slightly outperforms 2-hop Eclipse only when the reconfiguration delay is ridiculously large ($\delta =0.64$ unit of time); note that, as explained earlier, the idealized transmission time is 1 (unit of time)! In all other cases, 2-hop Eclipse performs much better than Eclipse++, and Eclipse++ performs only slightly better than Eclipse.

6 Related Work

6.1 Other Hybrid Switch Scheduling Algorithms

Liu et al. [19] first characterized the mathematical problem of the hybrid switch scheduling using direct routing only and proposed a greedy heuristic solution, called Solstice. In each iteration, Solstice effectively tries to find the Max-Min Weighted Matching (MMWM) in D, which is the full matching with the largest minimum element. The duration of this matching (configuration) is then set to this largest minimum element. Although its asymptotic computational complexity is a bit lower than Eclipse’s, our experiments show that its actual execution time is similar to Eclipse’s since Solstice has to compute a larger number of configurations K than Eclipse, which generally produces a tighter schedule.

This hybrid switching problem has also been considered in two other works [22, 23]. Their problem formulations are a bit different than that in [11, 19], and so are their solution approaches. In [22], matching senders with receivers is modeled as a stable marriage problem, in which a sender’s preference score for a receiver equals to the age of the data the former has to transmit to the latter in a scheduling epoch, and is solved using a variant of the Gale-Shapely algorithm [24]. This solution is aimed at minimizing transmission latencies while avoiding starvations, and not at maximizing network throughput, or equivalently minimizing transmission time. The innovations of [23] are mostly in the aspect of systems building and are not on matching algorithm designs.

To the best of our knowledge, Albedo [12] is the only other indirect routing solution for hybrid switching, besides Eclipse++ [11]. Albedo however solves a very different hybrid switching problem: when the traffic demand matrix D is not precisely known in advance and a sizable portion of it has to be estimated. It works as follows. Based on an estimation of D, Albedo first computes a direct routing schedule using Eclipse or Solstice. Then any unexpected “extra workload” resulting from the inaccurate estimation is routed indirectly. However, the computational complexity of Albedo, not mentioned in [12], appears at least as high as that of Eclipse++, because whereas Eclipse++ has to perform a shortest path computation for each VOQ (mentioned in Sect. 1.1), Albedo has to do so for each TCP/UDP flow belonging to the unexpected “extra workload”.

6.2 Optical Switch Scheduling Algorithms

Scheduling of circuit switch alone (i.e., no packet switch) has been studied for decades. Early works often assumed the reconfiguration delay to be either zero [9, 25] or infinity [26,27,28]. Further studies, like DOUBLE [26], ADJUST [10] and other algorithms such as [27, 29], take the actual reconfiguration delay into consideration. Recently, a solution called Adaptive MaxWeight (AMW) [30, 31] was proposed for optical switches (with nonzero reconfiguration delays). The basic idea of AMW is that when the maximum weighted configuration (matching) has a much higher weight than the current configuration, the optical switch is reconfigured to the maximum weighted configuration; otherwise, the configuration of the optimal switch stays the same. However, this algorithm may lead to long queueing delays (for packets) since it usually reconfigures infrequently.

7 Conclusion

In this paper, we propose 2-hop Eclipse, a hybrid switching algorithm that can jointly optimize both direct and 2-hop indirect routing. It is a slight but nontrivial modification of, has nearly the same asymptotical complexity as, and significantly outperforms the state of the art algorithm Eclipse, which optimizes only direct routing.