Abstract
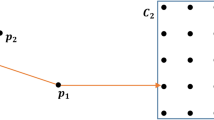
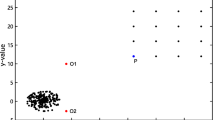
Outlier detection is an important task in data mining and has high practical value in numerous applications such as astronomical observation, text detection, fraud detection and so on. At present, a large number of popular outlier detection algorithms are available, including distribution-based, distance-based, density-based, and clustering-based approaches and so on. However, traditional outlier detection algorithms face some challenges. For one example, most distance-based and density-based outlier detection methods are based on k-nearest neighbors and therefore, are very sensitive to the value of k. For another example, some methods can only detect global outliers, but fail to detect local outliers. Last but not the least, most outlier detection algorithms do not accurately distinguish between boundary points and outliers. To partially solve these problems, in this paper, we propose to augment some boundary indicators to classical outlier detection algorithms. Experiments performed on both synthetic and real data sets demonstrate the efficacy of enhanced outlier detection algorithms.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Hawkins, D.M.: Identification of Outliers. Monographs on Applied Probability and Statistics. Chapman and Hall, London (1980)
Barnett, V., Lewis, T.: Outliers in Statistical Data, vol. 3. Wiley, New York (1994)
Knorr, E.M., Ng, R.T.: Algorithms for mining distance-based outliers in large datasets. In: Proceedings of the 24th VLDB Conference, New York, USA, pp. 392–403 (1998)
Breuning, M.M., Kriegel, H.P., Ng, R.T., Sander, J.: LOF: identifying density-based local outliers. In: Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, pp. 93–104 (2000)
Jiang, M.F., Tseng, S.S., Su, C.M.: Two-phase clustering process for outliers detection. Pattern Recogn. Lett. 22, 691–700 (2001)
Angiulli, F., Pizzuti, C.: Fast outlier detection in high dimensional spaces. In: Elomaa, T., Mannila, H., Toivonen, H. (eds.) PKDD 2002. LNCS, vol. 2431, pp. 15–27. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45681-3_2
Ramaswamy, S., Rastogi, R., Shim, K.: Efficient algorithms for mining outliers from large data sets. In: Proceedings of the ACM SIGMOD Conference, pp. 427–438 (2000)
Jin, W., Tung, A.K.H., Han, J., Wang, W.: Ranking outliers using symmetric neighborhood relationship. In: Ng, W.-K., Kitsuregawa, M., Li, J., Chang, K. (eds.) PAKDD 2006. LNCS (LNAI), vol. 3918, pp. 577–593. Springer, Heidelberg (2006). https://doi.org/10.1007/11731139_68
Huang, H., Mehrotra, K., Mohan, C.K.: Rank-based outlier detection. J. Stat. Comput. Simul. 83(3), 1–14 (2013)
UCI: The UCI KDD Archive, University of California, Irvine, CA. http://kdd.ics.uci.edu/
Aggarwal, C., Yu, P.: Outlier detection for high-dimensional data. In: Proceedings of the 2001 ACM SIGMOD Conference (SIGMOD 2001), Santa Barbara, CA, USA, pp. 37–46 (2001)
Acknowledgment
The authors would like to thank the Chinese National Science Foundation for its valuable support of this work under award 61473220 and all the anonymous reviewers for their valuable comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Li, X., Wang, X., Wang, X.L. (2018). Enhancing Outlier Detection by an Outlier Indicator. In: Perner, P. (eds) Machine Learning and Data Mining in Pattern Recognition. MLDM 2018. Lecture Notes in Computer Science(), vol 10934. Springer, Cham. https://doi.org/10.1007/978-3-319-96136-1_31
Download citation
DOI: https://doi.org/10.1007/978-3-319-96136-1_31
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96135-4
Online ISBN: 978-3-319-96136-1
eBook Packages: Computer ScienceComputer Science (R0)