Abstract
We propose new constrained pseudorandom functions (CPRFs) in traditional groups. Traditional groups mean cyclic and multiplicative groups of prime order that were widely used in the 1980s and 1990s (sometimes called “pairing free” groups). Our main constructions are as follows.
-
We propose a selectively single-key secure CPRF for circuits with depth \(O(\log n)\) (that is, NC\(^1\) circuits) in traditional groups where n is the input size. It is secure under the L-decisional Diffie-Hellman inversion (L-DDHI) assumption in the group of quadratic residues \(\mathbb {QR}_q\) and the decisional Diffie-Hellman (DDH) assumption in a traditional group of order q in the standard model.
-
We propose a selectively single-key private bit-fixing CPRF in traditional groups. It is secure under the DDH assumption in any prime-order cyclic group in the standard model.
-
We propose adaptively single-key secure CPRF for NC\(^1\) and private bit-fixing CPRF in the random oracle model.
To achieve the security in the standard model, we develop a new technique using correlated-input secure hash functions.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
1.1 Background
Pseudorandom functions (PRFs) are one of the most fundamental notions in cryptography [27]. A PRF is a deterministic function  where
where  ,
,  , and
, and  are its key space, domain, and range, respectively. Roughly speaking, we say that \(\mathsf {PRF}\) is a secure PRF if outputs of \(\mathsf {PRF}(\mathsf {msk},\cdot )\) look random for any input
are its key space, domain, and range, respectively. Roughly speaking, we say that \(\mathsf {PRF}\) is a secure PRF if outputs of \(\mathsf {PRF}(\mathsf {msk},\cdot )\) look random for any input  and a randomly chosen key
and a randomly chosen key  . Not only are PRFs used to construct secure encryption schemes but also they frequently appear in the constructions of various cryptographic primitives.
. Not only are PRFs used to construct secure encryption schemes but also they frequently appear in the constructions of various cryptographic primitives.
Constrained PRF. Boneh and Waters introduced the notion of constrained PRFs (CRPFs) [16] (Kiayias, Papadopoulos, Triandopoulos, and Zacharias [35] and Boyle, Goldwasser, and Ivan [10] also proposed the same notion in their concurrent and independent works). CPRFs are an advanced type of PRFs. Specifically, if we have a master secret key \(\mathsf {msk}\) of a CPRF \(\mathsf {PRF}\), then we can generate a “constrained” key \(\mathsf {sk}_f\) for a function  . We can compute the value \(\mathsf {PRF}(\mathsf {msk},x)\) from \(\mathsf {sk}_f\) and x if \(f(x) = 0\) holds; otherwise cannot. For an input x such that \(f(x) = 1\), the value \(\mathsf {PRF}(\mathsf {msk},x)\) looks pseudorandom.Footnote 1
. We can compute the value \(\mathsf {PRF}(\mathsf {msk},x)\) from \(\mathsf {sk}_f\) and x if \(f(x) = 0\) holds; otherwise cannot. For an input x such that \(f(x) = 1\), the value \(\mathsf {PRF}(\mathsf {msk},x)\) looks pseudorandom.Footnote 1
CPRFs with various types of function classes have been considered. Here, we explain the classes of bit-fixing functions and circuits since we present new CPRFs for these functions.
- Bit-fixing functions: :
-
Let \(\{0,1\}^n\) be the domain of a CPRF. Each function in this class is specified by a “constraint vector” \(c = (c_1,\dots ,c_n) \in \{0,1,*\}^n\), from which a bit-fixing function \(f_c: \{0,1\}^n \rightarrow \{0,1\}\) is defined as follows. If \(c_i = *\) or \(x_i = c_i\) holds for all \(i \in [n]\), then \(f_c(x) = 0\); otherwise \(f_c(x) = 1\).
- Circuits: :
-
This class consists of functions \(\{f_C\}\) computable by polynomial-sized boolean circuits C, defined by
 . We call a CPRF for this function class simply a CPRF for circuits. If a CPRF supports functions computable by polynomial-sized boolean circuits with depth \(O(\log n)\), where n is the input-length of the circuits, then we call it a CPRF for \({\mathbf {NC}}^1\).
. We call a CPRF for this function class simply a CPRF for circuits. If a CPRF supports functions computable by polynomial-sized boolean circuits with depth \(O(\log n)\), where n is the input-length of the circuits, then we call it a CPRF for \({\mathbf {NC}}^1\).
The number of constrained keys that can be released (to a potentially malicious party) is one of the important security measures of CPRFs. If a-priori unbounded polynomially many constrained keys could be released (i.e., the number of queries is not a-priori bounded), then a CPRF is called collusion-resistant. If only one constrained key can be released, it is called a single-key secure CPRF. Boneh and Waters [16] showed that (collusion-resistant) CPRFs have many applications such as broadcast encryption with optimal ciphertext length. (See their paper and references therein for more details.)
Private CPRF. Boneh, Lewi, and Wu [13] proposed the notion of privacy for CPRFs (Kiayias et al. also proposed policy privacy as essentially the same notion [35]). Roughly speaking, private CPRFs do not reveal information about constraints embedded in constrained keys beyond what is leaked from the evaluation results using the constrained keys.
Known instantiations. The first papers on CPRFs [10, 16, 35] observed that the Goldreich-Goldwasser-Micali [27] PRF yields a puncturable PRFFootnote 2 (and a CPRF for related simple functions). However, it turned out that achieving CPRFs for other types of function classes is quite challenging. Here, we review some prior works on CPRFs whose function classes are related to those we focus on in this study (i.e., bit-fixing functions and \({\mathbf {NC}}^1\) circuits).
Boneh and Waters [16] constructed a left-right CPRFFootnote 3 in the random oracle model (ROM) from bilinear maps, and a collusion-resistant bit-fixing CPRF and collusion-resistant CPRF for circuits from multilinear maps [25] in the standard model. After that, Brakerski and Vaikuntanathan [15] constructed a single-key secure CPRF for circuits from standard lattice-based assumptions, without relying on multilinear maps.
Boneh et al. [13] constructed a collusion-resistant private CPRF for circuits from indistinguishability obfuscation (IO) [9, 26], and a single-key private bit-fixing CPRF and puncturable CPRF from multilinear maps [13]. After that, a single-key private puncturable PRF [12], a single-key private CPRF for \({\mathbf {NC}}^1\) [18], and a single-key private CPRF for circuits [14, 37] were constructed from standard lattice assumptions.
Our motivation. (Private) CPRFs have been attracting growing attention as above since they are useful tools to construct various cryptographic primitives [13, 16]. A number of other types of CPRFs have been constructed [2, 8, 23, 32, 32, 33, 33]. However, all of known sufficiently expressive (private) CPRFs (such as bit-fixing, circuits) rely on IO, multilinear maps, or lattices, and there is currently no candidate of secure multilinear maps.
Very recently, Bitansky [11] and Goyal, Hohenberger, Koppula, and Waters [28] proposed sub-string matchFootnote 4 CPRFs in traditional groups to construct verifiable random functions. In this paper, by traditional groups we mean the multiplicative groups of prime orderFootnote 5 that have been widely used to construct various cryptographic primitives such as the ElGamal public-key encryption scheme, around two decades before bilinear maps dominate the area of cryptography [7]. (Of course, they are still being used for many cryptographic primitives.) However, their CPRFs are not expressive enough and do not satisfy the standard security requirements of CPRFsFootnote 6. See Tables 1 and 2 for comparisons. There is no construction of expressive enough (private) CPRF in traditional groups. This status might be reasonable since lattices and multilinear maps are stronger tools.
Based on the motivation mentioned above, we tackle the following question:
Is it possible to construct sufficiently expressive (private) CPRFs in traditional groups?
In this study, we give affirmative answers to this question and show that traditional groups are quite powerful tools. From the theoretical point of view, the more instantiations of cryptographic primitives are available, the more desirable. One reason is that constructions from different tools can be alternatives when one tool is broken (like multilinear maps). Another reason is that, generally, new instantiations shed light on how to construct the studied primitive, and widen and deepen our insights on it. One remarkable example of this line of research would be the recent work by Döttling and Garg [22], who constructed an identity-based encryption (IBE) scheme and a hierarchical IBE scheme in traditional groups. Another example would be the work by Boyle, Ishai, and Gilboa [17], who constructed communication-efficient secure two-party protocols in traditional groups. It is also expected that new instantiations provide us with insights on how to use the studied primitive in applications (in the real world or in the construction of another primitive as a building block).
1.2 Our Contributions
In this paper, we present new constructions of a CPRF and a private CPRF in traditional groups as main contributions.
The properties of our CPRFs are summarized as follows.
-
Our first CPRF is a selectively single-key secureFootnote 7 CPRF for NC\(^1\) in traditional groups. It is secure under the L-decisional Diffie-Hellman inversion (L-DDHI) assumptionFootnote 8 in the group of quadratic residues \(\mathbb {QR}_q\) and the decisional Diffie-Hellman (DDH) assumptionFootnote 9 in a traditional group \(\mathbb {G}\) of order q in the standard model. Here, \(\mathbb {QR}_q\) denotes the group of quadratic residue modulo q, where q is a prime such that \(q=2p+1\) and p is also a prime. We need to use this specific type of group for technical reasons. See Sects. 1.3 and 4 for the details.
-
Our second CPRF is a selectively single-key private bit-fixing CPRF in traditional groups. Specifically, it is secure under the standard DDH assumption in any prime-order cyclic group in the standard model.
-
Our third and fourth CPRFs are an adaptivelyFootnote 10 single-key secure CPRF for \({\mathbf {NC}}^1\) circuits and an adaptively single-key private bit-fixing CPRF, both in the ROM. Our standard model and ROM constructions of CPRFs for \({\mathbf {NC}}^1\), share high-level ideas behind the constructions in common, and the same is true for our bit-fixing CPRFs. These connections are explained in Sect. 1.3. Due to the space limit, we omit the constructions in the ROM in this paper.
The main technique that enables us to achieve the above results, is a novel use of correlated-input secure hash functions. We will explain the technical overview in Sect. 1.3.
As an application of our results, we can obtain a single-key secret-key attributed-based encryption (ABE) scheme with optimal ciphertext overhead in traditional groups. A (multi-key) public-key ABE scheme with optimal ciphertext overhead was presented by Zhandry [39], but it is based on multilinear maps. See the full version [3] for more details.
 ” column means the evaluation oracle is available for adversaries or not. “Tool” column means what kinds of cryptographic tools are used. GGM, pairing, and group mean the PRF by Goldreich, Goldwasser, and Micali [27], bilinear maps, and traditional groups, respectively. In “Assumptions” column, OWF, BDDH, LWE, and 1D-SIS mean one-way function, bilinear Diffie-Hellman, learning with errors, and one-dimensional short integer solution assumptions, respectively. In “Model” column, Std means the standard model. In “Misc” column, key-hom means key-homomorphic property.
” column means the evaluation oracle is available for adversaries or not. “Tool” column means what kinds of cryptographic tools are used. GGM, pairing, and group mean the PRF by Goldreich, Goldwasser, and Micali [27], bilinear maps, and traditional groups, respectively. In “Assumptions” column, OWF, BDDH, LWE, and 1D-SIS mean one-way function, bilinear Diffie-Hellman, learning with errors, and one-dimensional short integer solution assumptions, respectively. In “Model” column, Std means the standard model. In “Misc” column, key-hom means key-homomorphic property.1.3 Technical Overview
In this section, we provide an overview of our construction ideas. We ignore many subtle issues in this section and focus on the essential ideas for simplicity.
Basic construction satisfying no-evaluation security. To illustrate our ideas in a modular manner, we start with a no-evaluation secure CPRF for \({\mathbf {NC}}^1\), that is, adversaries do not have access to the evaluation oracle. We denote the PRF by \(\mathsf {PRF}_{\mathsf {NE}}\). It turns out that even in this simple setting, it is non-trivial to construct a CPRF for \({\mathbf {NC}}^1\) in traditional groups (or bilinear groups) since known constructions use some sort of “fully homomorphic” properties of lattices or multilinear maps, both of which are not available in traditional groups. In the following, let \(\lambda \) be the security parameter.
The first challenge is how to implement an \({\mathbf {NC}}^1\) circuit constraint in a key. Our idea is to encode an \({\mathbf {NC}}^1\) circuit fFootnote 11 into a bit string \(f=(f_1,\ldots ,f_z) \in \{0,1\}^{z}\) and then embed this into a secret key. When evaluating a PRF value on input \(x=(x_1,\ldots , x_n)\in \{0,1\}^n\), we will “homomorphically” evaluate \(U(\cdot , x)\) on the secret key, where \(U(\cdot , \cdot )\) is a universal circuit that outputs \(U(f,x) = f(x)\) on input (f, x). To make the representation of the universal circuit \(U(\cdot , \cdot )\) compatible with our algebraic setting, we regard \(U(\cdot ,\cdot )\) as a degree-D polynomial of the variables \(\{ f_i \}\) and \(\{ x_j \}\), such that D is some fixed polynomial of \(\lambda \).Footnote 12 Furthermore, we extend the input space of \(U(\cdot , \cdot )\) to be non-binary, where the computation is done over \(\mathbb {Z}_p\) using the polynomial representation of \(U(\cdot , \cdot )\). Specifically, we allow the input of the form \(((b_1,\ldots , b_z),x)\in \mathbb {Z}_p^{z} \times \{0,1\}^n\).
Now, we give a more detailed description of \(\mathsf {PRF}_{\mathsf {NE}}\). A master secret key \(\mathsf {msk}\) of \(\mathsf {PRF}_{\mathsf {NE}}\) is of the form \((b_1,\ldots ,b_z,\alpha ,g)\), where \(b_i \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_p\) for each \(i \in [z]\) and \(\alpha \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}^*_p\), and g is a generator of a traditional group \(\mathbb {H}\) of order p. (We will turn to the explanation on this group \(\mathbb {H}\) later in this subsection.) The evaluation algorithm of \(\mathsf {PRF}_{\mathsf {NE}}\) outputs \(g^{x'/\alpha }\), where \(x' = U((b_1,\ldots ,b_z),x) \in \mathbb {Z}_p\). To compute a constrained key \(\mathsf {sk}_f\) of an \({\mathbf {NC}}^1\) circuit f, we set  . The constrained key is \(\mathsf {sk}_f =(f,b'_1,\ldots ,b'_z,g,g^{\alpha },g^{\alpha ^2},\ldots ,g^{\alpha ^{D-1}})\).
. The constrained key is \(\mathsf {sk}_f =(f,b'_1,\ldots ,b'_z,g,g^{\alpha },g^{\alpha ^2},\ldots ,g^{\alpha ^{D-1}})\).
We then look closer at why this construction achieves the constraint defined by the \({\mathbf {NC}}^1\) circuit f. When we compute  by using \(b_i = \alpha \cdot b'_i + f_i\), we can write the computation of U in the following way:
by using \(b_i = \alpha \cdot b'_i + f_i\), we can write the computation of U in the following way:
where the coefficients \(\{c_j\}_j\) are efficiently computable from the descriptions of U and f, \(\{b'_i\}_i\), and x since the degree D is polynomial in the security parameter. This can be seen by observing that \(U((\alpha \cdot b'_1 + f_1,\ldots ,\alpha \cdot b'_z+ f_z),x)\) should be equal to f(x) when \(\alpha =0\) since we have \(U((f_1,\ldots ,f_z),x)=f(x)\) by the definition of a universal circuit.
-
If \(f(x)=0\), then we can compute \(g^{x'/\alpha } = g^{f(x)/\alpha + \sum _{j=0}^{D-1}c_j \alpha ^j}\) since the \(g^{f(x)/\alpha }\) part disappears and the remaining part is computable from \(\mathsf {sk}_f = (f,b'_1,\ldots ,b'_z,g,g^{\alpha },\ldots ,g^{\alpha ^{D-1}})\) and x.
-
If \(f(x)=1\), then \(g^{x'/\alpha } = g^{f(x)/\alpha + \sum _{j=0}^{D-1}c_j \alpha ^j}\) looks random since \(g^{1/\alpha }\) looks random even if \((g,g^{\alpha },\ldots ,g^{\alpha ^{D-1}})\) is given, due to the \((D-1)\)-DDHI assumption in \(\mathbb {H}\).
This is a high-level intuition for why \(\mathsf {PRF}_{\mathsf {NE}}\) for \({\mathbf {NC}}^1\) is no-evaluation secure. This CPRF \(\mathsf {PRF}_{\mathsf {NE}}\) is our base construction, and the idea behind our construction here is inspired by the affine partitioning function used in the recent construction of a verifiable random function by Yamada [38].
On the other hand, this construction can be broken by making only one evaluation query: Suppose that \(x\not =\widehat{x}\) satisfy \(f(x)=f(\widehat{x})=1\). Then we can write \(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},x)= g^{1/\alpha + \sum _{j=0}^{D-1}c_j \alpha ^j}\) and \(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},\widehat{x})= g^{1/\alpha + \sum _{j=0}^{D-1}\widehat{c_j} \alpha ^j}\) by using \(\{c_j\}_j\) and \(\{\widehat{c_j}\}_j\) that are efficiently computable by an adversary. Then we have  . Therefore if an adversary obtains \(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},x)\), then it can efficiently compute \(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},\widehat{x})\) and break the security of the PRF.
. Therefore if an adversary obtains \(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},x)\), then it can efficiently compute \(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},\widehat{x})\) and break the security of the PRF.
Single-key secure construction in the ROM. To achieve security against adversaries making a-priori unbounded polynomially many evaluation queries (i.e., the number of queries is polynomial, but not fixed in advance), we consider using a random oracle as an intermediate step. (This construction is denoted by \(\mathsf {PRF}^{\mathsf {rom}}\).) \(\mathsf {PRF}^{\mathsf {rom}}\) is the same as \(\mathsf {PRF}_{\mathsf {NE}}\) except that an output is now computed by \(H(g^{x'/\alpha })\), instead of \(g^{x'/\alpha }\), where \(H: \mathbb {H}\rightarrow \{0,1\}^{n'}\) is a cryptographic hash function. In the ROM where H is modeled as a random oracle, adversaries make hash queries and obtain outputs of the hash function H. If \(f(x)=1\), then an adversary cannot compute \(g^{x'/\alpha }\) due to the no-evaluation security, and thus \(H(g^{x'/\alpha })\) seems uniformly random from the view of the adversary. Therefore evaluation queries from an adversary can be answered with uniformly random strings, and the adversary cannot notice whether this is a correct behavior of the evaluation oracle as long as it does not find a collision \((x_1,x_2)\) such that \(g^{x'_1/\alpha } = g^{x'_2/\alpha }\) where \(x'_i = U((b_1,\ldots ,b_z),x_i)\). Our real construction is slightly modified from the above construction so that such a collision exists only with negligible probability (see Sect. 4.1 for the detail).
The second challenge is how to remove the random oracle and achieve security against a-priori unbounded polynomially evaluation queries in the standard model.
Replacing a random oracle with a correlated-input secure hash function. We observe that we do not need the full power of random oracles to prove the security of CPRFs. Specifically, we can use a correlated-input secure hash function (CIH) [5, 29, 30, 34]Footnote 13, instead of random oracles.
Here, we briefly recall the definition of a CIH whose definition is associated with a class of functions \(\varPsi \). At the beginning, the challenger chooses the challenge bit \(\mathsf {coin}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\{0,1\}\), a function description \(\mathsf {CIH}\),Footnote 14 and a random element r from the domain of \(\mathsf {CIH}\). The adversary is given \(\mathsf {CIH}\) and access to an oracle that, upon a query \(\psi _i \in \varPsi \) from the adversary, answers \(\mathsf {CIH}(\psi _i(r))\) if \(\mathsf {coin}=1\); otherwise the oracle answers the query with \(\mathsf {RF}(\psi _i(r))\), where \(\mathsf {RF}\) is a truly random function. If it is hard for adversaries to distinguish the case \(\mathsf {coin}=1\) from the case \(\mathsf {coin}=0\), we say that \(\mathsf {CIH}\) is correlated-input pseudorandom for \(\varPsi \) (or simply, a CIH for \(\varPsi \)).Footnote 15
If there exists a CIH for group-induced functions \(\psi _{\varDelta }: \mathbb {H}\rightarrow \mathbb {H}\) such that \(\varDelta \in \mathbb {H}\) and  (denoted by \(\mathsf {CIH}_{0}\)) where \(\cdot \) is the group operation of \(\mathbb {H}\), then \(\mathsf {CIH}_{0}(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},x))\) is a secure CPRF. This can be seen as follows: For x satisfying \(f(x)=1\), \(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},x)\) can be written as \(g^{1/\alpha }\cdot g^{\sum _{j=0}^{D-1}c_j \alpha ^j}\) where \(g^{1/\alpha }\) is pseudorandom and \(g^{\sum _{j=0}^{D-1}c_j \alpha ^j}\) is efficiently computable from the view of an adversary as discussed above. By applying the security of a CIH by setting
(denoted by \(\mathsf {CIH}_{0}\)) where \(\cdot \) is the group operation of \(\mathbb {H}\), then \(\mathsf {CIH}_{0}(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},x))\) is a secure CPRF. This can be seen as follows: For x satisfying \(f(x)=1\), \(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},x)\) can be written as \(g^{1/\alpha }\cdot g^{\sum _{j=0}^{D-1}c_j \alpha ^j}\) where \(g^{1/\alpha }\) is pseudorandom and \(g^{\sum _{j=0}^{D-1}c_j \alpha ^j}\) is efficiently computable from the view of an adversary as discussed above. By applying the security of a CIH by setting  and \(\varDelta = g^{\sum _{j=0}^{D-1}c_j \alpha ^j}\), we can see that \(\mathsf {CIH}_{0}(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},x))\) is computationally indistinguishable from \(\mathsf {RF}(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},x))\). This is computationally indistinguishable from a random function as long as \(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},x)\) has no collision, and the actual construction of \(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},x)\) is made collision-free as mentioned in the previous paragraph.
and \(\varDelta = g^{\sum _{j=0}^{D-1}c_j \alpha ^j}\), we can see that \(\mathsf {CIH}_{0}(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},x))\) is computationally indistinguishable from \(\mathsf {RF}(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},x))\). This is computationally indistinguishable from a random function as long as \(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},x)\) has no collision, and the actual construction of \(\mathsf {PRF}_{\mathsf {NE}}(\mathsf {msk},x)\) is made collision-free as mentioned in the previous paragraph.
However, there is one subtle issue: The only known instantiation of CIH for group induced functions which satisfies our security requirements is the CIH based on the DDH assumption by Bellare and Cash [5] (denoted by \(\mathsf {CIH}_{\mathsf {BC} }\)). In \(\mathsf {CIH}_{\mathsf {BC} }\), we consider the m-dimensional, component-wise group-induced functions  , where \(\psi _{\vec {a}} : (\mathbb {Z}_q^*)^m \rightarrow (\mathbb {Z}_q^*)^m\) is defined by
, where \(\psi _{\vec {a}} : (\mathbb {Z}_q^*)^m \rightarrow (\mathbb {Z}_q^*)^m\) is defined by  and \(\star \) denotes the component-wise group operation on \(\mathbb {Z}_q^*\). Here, the domain of \(\mathsf {CIH}_{\mathsf {BC} }\) is not compatible with the range of \(\mathsf {PRF}_{\mathsf {NE}}\) (the output is \(g^{x'/\alpha _i} \in \mathbb {H}\)). One might think that m-folded parallel running of \(\mathsf {PRF}_{\mathsf {NE}}\) on
and \(\star \) denotes the component-wise group operation on \(\mathbb {Z}_q^*\). Here, the domain of \(\mathsf {CIH}_{\mathsf {BC} }\) is not compatible with the range of \(\mathsf {PRF}_{\mathsf {NE}}\) (the output is \(g^{x'/\alpha _i} \in \mathbb {H}\)). One might think that m-folded parallel running of \(\mathsf {PRF}_{\mathsf {NE}}\) on  works, but this is not the case. This is because if
works, but this is not the case. This is because if  , then the L-DDHI assumption can be easily broken by computing the Jacobi symbol.
, then the L-DDHI assumption can be easily broken by computing the Jacobi symbol.
We observe that the attack based on the Jacobi symbol does not work if we consider the group of quadratic residues modulo q, denoted by \(\mathbb {QR}_q\) instead of \(\mathbb {Z}_q^*\), and it is reasonable to assume the L-DDHI assumption holds on \(\mathbb {QR}_q\). However, if we set  , then we cannot simply use the security of \(\mathsf {CIH}_{\mathsf {BC} }\) since it is not obvious if the security of \(\mathsf {CIH}_{\mathsf {BC} }\) still holds when we restrict the domain of \(\mathsf {CIH}_{\mathsf {BC} }\) to \(\mathbb {QR}_q^m\). We resolve the issue by proving that the CIH obtained by restricting the domain of \(\mathsf {CIH}_{\mathsf {BC} }\) to \(\mathbb {QR}_q^m\) (denoted by \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} \)) is also secure as a CIH for component-wise group operations on \(\mathbb {QR}_q^m\) under the DDH assumption on a group of an order \(p=\frac{q-1}{2}\) if p is a prime. See Sect. 3 for more details of \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} \).
, then we cannot simply use the security of \(\mathsf {CIH}_{\mathsf {BC} }\) since it is not obvious if the security of \(\mathsf {CIH}_{\mathsf {BC} }\) still holds when we restrict the domain of \(\mathsf {CIH}_{\mathsf {BC} }\) to \(\mathbb {QR}_q^m\). We resolve the issue by proving that the CIH obtained by restricting the domain of \(\mathsf {CIH}_{\mathsf {BC} }\) to \(\mathbb {QR}_q^m\) (denoted by \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} \)) is also secure as a CIH for component-wise group operations on \(\mathbb {QR}_q^m\) under the DDH assumption on a group of an order \(p=\frac{q-1}{2}\) if p is a prime. See Sect. 3 for more details of \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} \).
We are now ready to explain our CRPF \(\mathsf {PRF}\) for \({\mathbf {NC}}^1\). It uses multiple instances of \(\mathsf {PRF}_{\mathsf {NE}}\) and apply a CIH for m-dimensional component-wise group-induced functions to the outputs from those instances. That is, we define

Now, we look closer at why correlated-input pseudorandomness helps us achieve security in the presence of a-priori unbounded polynomially many evaluation queries. In \(\mathsf {PRF}_{\mathsf {NE}}\), when the inputs x with \(f(x)=1\) are used, we can view its output as consisting of two separate parts. Specifically, we can write \(g^{x'/\alpha } = g^{f(x)/\alpha + \sum _{j=0}^{D-1}c_j \alpha ^j} = \mathsf {Aux}(\mathsf {msk})\cdot \mathsf {SEval}(\mathsf {sk}_f,x)\) if we define  and
and  (where \(\mathsf {SEval}\) stands for “semi”-evaluation). The first part is computable only from \(\mathsf {msk}\), and the second part is computable from \(\mathsf {sk}_f\) and x. Thanks to the \((D-1)\)-DDHI assumption, it is now easy to see that \(\mathsf {Aux}(\mathsf {msk})\) is indistinguishable from a random element even if \(\mathsf {sk}_f\) is given. Therefore, it holds that
(where \(\mathsf {SEval}\) stands for “semi”-evaluation). The first part is computable only from \(\mathsf {msk}\), and the second part is computable from \(\mathsf {sk}_f\) and x. Thanks to the \((D-1)\)-DDHI assumption, it is now easy to see that \(\mathsf {Aux}(\mathsf {msk})\) is indistinguishable from a random element even if \(\mathsf {sk}_f\) is given. Therefore, it holds that
where \(r_i \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {H}\) for all \(i \in [m]\) and \(\approx _{\mathsf {c}}\) denotes computational indistinguishability. Furthermore, \(\mathsf {sk}_{f,i}\) denotes the secret key associated to f generated from \(\mathsf {msk}_i\). (Namely, it corresponds to the i-th instance.) Here,  are adversarially chosen correlated values and fall in the component-wise group-induced functions \(\varPsi ^{\mathsf {g}\text {-}\mathsf {indc}}_m\) due to \((\phi _1,\ldots , \phi _m) \in \mathbb {H}^m\). Therefore, by applying the correlated-input pseudorandomness of \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} \), we obtain
are adversarially chosen correlated values and fall in the component-wise group-induced functions \(\varPsi ^{\mathsf {g}\text {-}\mathsf {indc}}_m\) due to \((\phi _1,\ldots , \phi _m) \in \mathbb {H}^m\). Therefore, by applying the correlated-input pseudorandomness of \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} \), we obtain
As long as adversaries do not find a collision \((x_1,x_2)\) such that \((\mathsf {SEval}(\mathsf {sk}_{ f,1},x_1),\ldots ,\mathsf {SEval}(\mathsf {sk}_{f, m},x_1)) = (\mathsf {SEval}(\mathsf {sk}_{f, 1},x_2),\ldots ,\mathsf {SEval}(\mathsf {sk}_{f,m},x_2))\), \(\mathsf {PRF}_{{\mathbf {NC}}^1}(\mathsf {msk}, \cdot )\) is pseudorandom since \(\mathsf {RF}\) is a truly random function. It is not difficult to see that a collision is hard to find by the universality of the modified \(\mathsf {PRF}_{\mathsf {NE}}\) (see Lemma 8 for the detail). Therefore, we can prove the pseudorandomness of \(\mathsf {PRF}\) against a-priori unbounded polynomially many evaluation queries in the standard model by using the security of CIH for (m-dimensional, component-wise) group-induced functions.
How to achieve private constraint. Here, we give a brief explanation on how our single-key private CPRF for bit-fixing functions is constructed. The basic strategy is the same as that of our CPRFs for \({\mathbf {NC}}^1\). That is, we firstly construct a private bit-fixing CPRF in the ROM, and then convert it into a private bit-fixing CPRF in the standard model via a CIH for an appropriate function class.
Our single-key private bit-fixing CPRF in the ROM is very simple. This is slightly different from what we present in the full version of this paper [3], but we stick to the following construction in this section since it is consistent with the standard model construction in Sect. 5.1. A master secret key is  and a PRF output for input x is \(H(\sum _{i=1}^{n}s_{i,x_i})\) where H is a (standard) hash function. For convenience, we define
and a PRF output for input x is \(H(\sum _{i=1}^{n}s_{i,x_i})\) where H is a (standard) hash function. For convenience, we define  . A constrained key for \(c\in \{0,1,*\}^n\) is \(\{t_{i,b}\}_{i\in [n],b\in \{0,1\}}\) where
. A constrained key for \(c\in \{0,1,*\}^n\) is \(\{t_{i,b}\}_{i\in [n],b\in \{0,1\}}\) where  if \(c_i =*\) or \(c_i =b\); otherwise \(t_{i,b} \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_p\). If an input does not match the constraint c, then the sum includes completely unrelated values and we cannot compute the correct output. Adversaries are given just random values by the random oracle. Moreover, adversaries cannot distinguish two different constraints as long as a challenge input does not satisfy the constraints since both \(s_{i,b}\) and \(t_{i,b}\) are uniformly random values in \(\mathbb {Z}_p\). This construction satisfies adaptive single-key privacy in the random oracle model, without relying on any complexity assumption.
if \(c_i =*\) or \(c_i =b\); otherwise \(t_{i,b} \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_p\). If an input does not match the constraint c, then the sum includes completely unrelated values and we cannot compute the correct output. Adversaries are given just random values by the random oracle. Moreover, adversaries cannot distinguish two different constraints as long as a challenge input does not satisfy the constraints since both \(s_{i,b}\) and \(t_{i,b}\) are uniformly random values in \(\mathbb {Z}_p\). This construction satisfies adaptive single-key privacy in the random oracle model, without relying on any complexity assumption.
Now we replace the cryptographic hash function (random oracle) H with a CIH \(\mathsf {CIH}_\mathsf {aff}\) for affine functions \(\varPhi ^{\mathsf {aff}}= \{\phi _{\vec {u},\vec {v}} : \mathbb {Z}_p^m \rightarrow \mathbb {Z}_p^m \}\) where \(\vec {u} \in (\mathbb {Z}^*_p)^m\), \(\vec {v}\in \mathbb {Z}_p^m\), and  where \(\odot \) is component-wise multiplication in \(\mathbb {Z}_p\). Our private bit-fixing CPRF is defined by
where \(\odot \) is component-wise multiplication in \(\mathbb {Z}_p\). Our private bit-fixing CPRF is defined by

A constrained key \(\mathsf {sk}_c\) consists of constrained keys for c with respect to \(\mathsf {msk}_j\), for all \(j\in [m]\). It is easy to see that the correctness holds. For the security, we set  for \(c_i \ne *\) and \(b = 1 -c_i\) where \(\alpha _j \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_p\). Then, we can write \(\sum _{i=1}^{n} s_{i,x_i,j} = u \alpha _j + v_j\) for some \(u \in [n]\) (especially \(u\not =0\)) where \(v_j = \sum _{i=1}^{n}t_{i,x_i,j}\) for an evaluation query x from an adversary, since x is not allowed to satisfy the constraint. For two different constraints, the adversary cannot distinguish which constraint is used in a constrained key (that is, \(s_{i,b,j} \approx _{\mathsf {c}}t_{i,b,j} + \alpha _j\)) since \(t_{i,b,j}\) is uniformly random. Here, \(\alpha _j\)’s are uniformly random and u and \(v_j\) are adversarially chosen values. It is easy to see that this falls into the class of affine functions. Thus, we can use the security of the CIH \(\mathsf {CIH}_\mathsf {aff}\) for affine functions, and obtain
for \(c_i \ne *\) and \(b = 1 -c_i\) where \(\alpha _j \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_p\). Then, we can write \(\sum _{i=1}^{n} s_{i,x_i,j} = u \alpha _j + v_j\) for some \(u \in [n]\) (especially \(u\not =0\)) where \(v_j = \sum _{i=1}^{n}t_{i,x_i,j}\) for an evaluation query x from an adversary, since x is not allowed to satisfy the constraint. For two different constraints, the adversary cannot distinguish which constraint is used in a constrained key (that is, \(s_{i,b,j} \approx _{\mathsf {c}}t_{i,b,j} + \alpha _j\)) since \(t_{i,b,j}\) is uniformly random. Here, \(\alpha _j\)’s are uniformly random and u and \(v_j\) are adversarially chosen values. It is easy to see that this falls into the class of affine functions. Thus, we can use the security of the CIH \(\mathsf {CIH}_\mathsf {aff}\) for affine functions, and obtain
As long as a collision of \((\mathsf {PRF}_{\mathsf {bf}\text {-}\mathsf {NE}}(\mathsf {msk}_1,\cdot ),\ldots ,\mathsf {PRF}_{\mathsf {bf}\text {-}\mathsf {NE}}(\mathsf {msk}_m,\cdot )\) is not found, \(\mathsf {RF}(u \alpha _1 + v_1,\ldots ,u \alpha _m + v_m)\) is indistinguishable from a random value. Furthermore, it is not difficult to show that the condition holds by the universality of  . Therefore, we can prove the security of our private bit-fixing CPRF. See the full version of this paper [3] for the details.
. Therefore, we can prove the security of our private bit-fixing CPRF. See the full version of this paper [3] for the details.
1.4 Other Related Works
While we focus on (private) CPRFs without IO and multilinear maps, many expressive (private) CPRFs have been proposed based on IO or multilinear maps: collusion-resistant CPRFs for circuit based on multilinear maps [8, 16], adaptively secure CPRFs based on IO [32, 33], collusion-resistant CPRFs for Turing machines based on (differing-input) IO [2, 23], collusion-resistant private CPRFs for circuits based on IO [13].
Cohen, Goldwasser, and Vaikuntanathan showed a connection between CPRFs for some class of functions and computational learning theory [19]. See the papers and references therein for more details.
Organization. The rest of the paper is organized as follows. After introducing minimum notations, security definitions, and building blocks in Sect. 2, we present our correlated-input secure hash function in Sect. 3, our CPRFs for \({\mathbf {NC}}^1\) and its security proofs in Sect. 4, and our private bit-fixing CPRF in Sect. 5. Many materials are omitted in this extended abstract due to the space limit. See the full version for all details [3].
2 Preliminaries
In this section, we review some notations and definitions, tools, and cryptographic primitives.
Notations. We denote by “\(\mathrm {poly}(\cdot )\)” an unspecified integer-valued positive polynomial of \(\lambda \) and by “\(\mathrm {negl}(\lambda )\)” an unspecified negligible function of \(\lambda \). For sets \(\mathcal {D}\) and \(\mathcal {R}\), “\(\mathsf {Func}(\mathcal {D},\mathcal {R})\)” denotes the set of all functions with domain \(\mathcal {D}\) and range \(\mathcal {R}\).
Group generator. For convenience, we introduce the notion of a “group generator”. We say that a PPT algorithm \(\mathsf {GGen}\) is a group generator, if it takes a security parameter \(1^{\lambda }\) as input and outputs a “group description”  where \(\mathbb {G}\) is a group with prime order \(p = \varOmega (2^{\lambda })\), from which one can efficiently sample a generator uniformly at random.
where \(\mathbb {G}\) is a group with prime order \(p = \varOmega (2^{\lambda })\), from which one can efficiently sample a generator uniformly at random.
2.1 Constrained Pseudorandom Function
Here, we give the syntax and security definitions for a constrained pseudorandom function (CPRF). For clarity, we will define a CPRF as a primitive that has a public parameter. However, this treatment is compatible with the standard syntax in which there is no public parameter, because it can always be contained as part of a master secret key and constrained secret keys.
Syntax. Let \(\mathcal {F}= \{\mathcal {F}_{\lambda ,k}\}_{\lambda ,k \in \mathbb {N}}\) be a class of functionsFootnote 16 where each \(\mathcal {F}_{\lambda ,k}\) is a set of functions with domain \(\{0,1\}^k\) and range \(\{0,1\}\), and the description size (when represented by a circuit) of every function in \(\mathcal {F}_{\lambda ,k}\) is bounded by \(\mathrm {poly}(\lambda ,k)\).
A CPRF for \(\mathcal {F}\) consists of the five PPT algorithms \((\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Eval}, \mathsf {Constrain}, \mathsf {CEval})\) where \((\mathsf {Setup},\mathsf {KeyGen},\mathsf {Eval})\) constitutes a PRF (where a key \(\mathsf {msk}\) output by \(\mathsf {KeyGen}\) is called a master secret key), and the last two algorithms \(\mathsf {Constrain}\) and \(\mathsf {CEval}\) have the following interfaces:
- \(\mathsf {Constrain}(\mathsf {pp}, \mathsf {msk}, f) \overset{\scriptscriptstyle \mathsf {R}}{\rightarrow }\mathsf {sk}_f\)::
-
This is the constraining algorithm that takes as input a public parameter \(\mathsf {pp}\), a master secret key \(\mathsf {msk}\), and a function \(f \in \mathcal {F}_{\lambda ,n}\), where \(n = n(\lambda ) = \mathrm {poly}(\lambda )\) is the input-length specified by \(\mathsf {pp}\). Then, it outputs a constrained key \(\mathsf {sk}_f\).
 ::
::-
This is the deterministic constrained evaluation algorithm that takes a public parameter \(\mathsf {pp}\), a constrained key \(\mathsf {sk}_f\), and an element \(x \in \{0,1\}^n\) as input, and outputs an element \(y \in \mathcal {R}\).
As in an ordinary PRF, whenever clear from the context, we will drop \(\mathsf {pp}\) from the inputs of \(\mathsf {Eval}\), \(\mathsf {Constrain}\), and \(\mathsf {CEval}\), and the executions of them are denoted as “\(\mathsf {Eval}(\mathsf {msk},x)\)”, “\(\mathsf {Constrain}(\mathsf {msk},f)\)”, and “\(\mathsf {CEval}(\mathsf {sk}_f, x)\)”, respectively.
Correctness. For correctness of a CPRF for a function class \(\mathcal {F}= \{\mathcal {F}_{\lambda ,k}\}_{\lambda ,k\in \mathbb {N}}\), we require that for all \(\lambda \in \mathbb {N}\), \(\mathsf {pp}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {Setup}(1^{\lambda })\) (which specifies the input length \(n = n(\lambda ) = \mathrm {poly}(\lambda )\)), \(\mathsf {msk}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {KeyGen}(\mathsf {pp})\), functions \(f \in \mathcal {F}_{\lambda ,n}\), and inputs \(x \in \{0,1\}^n\) satisfying \(f(x) = 0\), we have \(\mathsf {CEval}(~\mathsf {Constrain}(\mathsf {msk},f),x~) = \mathsf {Eval}(\mathsf {msk},x)\).
Remark 1
We note that in our definition, the role of the constraining functions f is “reversed” from that in the original definition [16], in the sense that correctness (i.e. the equivalence \(\mathsf {Eval}(\mathsf {msk}, \cdot ) = \mathsf {CEval}(\mathsf {sk}_f, \cdot )\)) is required for inputs x with \(f(x) = 0\), while it is required for inputs x with \(f(x) = 1\) in the original definition [16].
Security. Here, we give the security definitions for a CPRF. We only consider CPRFs that are secure in the presence of a single constrained key, for which we consider two flavors of security: selective single-key security and adaptive single-key security. The former notion only captures security against adversaries \(\mathcal {A}\) that decide the constraining function f (and the constrained key \(\mathsf {sk}_f\) is given to \(\mathcal {A}\)) before seeing any evaluation result of the CPRF, while the latter notion has no such restriction and captures security against adversaries that may decide the constraining function f at any time. Also, in Sect. 4, as a security notion for a CPRF used as a building block, we will use the notion of no-evaluation security, which captures security against adversaries that have no access to the evaluation oracle. The definition below reflects these differences.
Formally, for a CPRF \(\mathsf {CPRF}= (\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Eval}, \mathsf {Constrain}, \mathsf {CEval})\) (with input-length \(n = n(\lambda )\)) for a function class \(\mathcal {F}= \{\mathcal {F}_{\lambda ,k}\}_{\lambda ,k \in \mathbb {N}}\) and an adversary \(\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)\), we define the single-key security experiment  as described in Fig. 1 (left).
as described in Fig. 1 (left).
In the security experiment, the adversary \(\mathcal {A}\)’s single constraining query is captured by the function f included in the first-stage algorithm \(\mathcal {A}_1\)’s output. Furthermore, \(\mathcal {A}_1\) and \(\mathcal {A}_2\) have access to the challenge oracle \(\mathcal {O}_{\mathsf {Chal}}(\cdot )\) and the evaluation oracle \(\mathsf {Eval}(\mathsf {msk},\cdot )\), where the former oracle takes \(x^* \in \{0,1\}^n\) as input, and returns either the actual evaluation result \(\mathsf {Eval}(\mathsf {msk}, x^*)\) or the output \(\mathsf {RF}(x^*)\) of a random function, depending on the challenge bit \(\mathsf {coin}\in \{0,1\}\).
We say that an adversary \(\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)\) in the security experiment \(\mathsf {Expt}_{\mathsf {CPRF},\mathcal {F},n,\mathcal {A}}^{\mathsf {cprf}}(\lambda )\) is admissible if \(\mathcal {A}_1\) and \(\mathcal {A}_2\) are PPT and respect the following restrictions:
-
\(f \in \mathcal {F}_{\lambda ,n}\).
-
\(\mathcal {A}_1\) and \(\mathcal {A}_2\) never make the same query twice.
-
All challenge queries \(x^*\) made by \(\mathcal {A}_1\) and \(\mathcal {A}_2\) satisfy \(f(x^*) = 1\), and are distinct from any of the evaluation queries x that they submit to the evaluation oracle \(\mathsf {Eval}(\mathsf {msk},\cdot )\).
Furthermore, we say that \(\mathcal {A}\) is selectively admissible if, in addition to the above restrictions, \(\mathcal {A}_1\) makes no challenge or evaluation queries. Finally, we say that \(\mathcal {A}\) is a no-evaluation adversary if \(\mathcal {A}_1\) and \(\mathcal {A}_2\) are PPT, and they do not make any queries, except that \(\mathcal {A}_2\) is allowed to make only a single challenge query \(x^*\) such that \(f(x^*) = 1\).
Definition 1
(Security of CPRF). We say that a CPRF \(\mathsf {CPRF}\) for a function class \(\mathcal {F}\) is adaptively single-key secure, if for all admissible adversaries \(\mathcal {A}\), the advantage  is negligible.
is negligible.
We define selective single-key security (resp. no-evaluation security) of \(\mathsf {CPRF}\) analogously, by replacing the phrase “all admissible adversaries \(\mathcal {A}\)” in the above definition with “all selectively admissible adversaries \(\mathcal {A}\)” (resp. “all no-evaluation adversaries \(\mathcal {A}\)”).
Remark 2
As noted by Boneh and Waters [16], without loss of generality we can assume that \(\mathcal {A}\) makes a challenge query only once, because security for a single challenge query can be shown to imply security for multiple challenge queries via a standard hybrid argument. Hence, in the rest of the paper we only use the security experiment with a single challenge query for simplicity.
Remark 3
In some existing works [16, 23, 24], the term “selective” is used to mean that \(\mathcal {A}\) has to make a challenge query at the beginning of the security experiment. On the other hand, in this paper, “selective” means that \(\mathcal {A}\) has to make a constraining query at the beginning of the security experiment, which is the same definitional approach by Brakerski and Vaikuntanathan [15].
2.2 Correlated-Input Secure Hash Function
Here, we review the definition of a correlated-input secure hash function (CIH) that was originally introduced in Goyal et al. [30].
Syntactically, a CIH is an efficiently computable deterministic (hash) function that has a public parameter \(\mathsf {pp}\) that is generated by using some setup procedure, and we refer to such a pair of function and setup procedure as a publicly parameterized function. In this paper, we will consider a CIH that is associated with a group generator \(\mathsf {GGen}\). Thus, we model its setup algorithm by a “parameter generation” algorithm \(\mathsf {PrmGen}\) that takes a group description \(\mathcal {G}\) generated by \(\mathsf {GGen}\) as input, and outputs a public parameter \(\mathsf {pp}\).
Formally, a publicly parameterized function \(\mathsf {CIH}\) with respect to a group generator \(\mathsf {GGen}\), consists of the two PPT algorithms \((\mathsf {PrmGen}, \mathsf {Eval})\) with the following interfaces:
- \(\mathsf {PrmGen}(\mathcal {G}) \overset{\scriptscriptstyle \mathsf {R}}{\rightarrow }\mathsf {pp}\)::
-
This is the parameter generation algorithm that takes as input a group description \(\mathcal {G}\) output by \(\mathsf {GGen}(1^{\lambda })\). Then, it outputs a public parameter \(\mathsf {pp}\), where we assume that \(\mathsf {pp}\) contains \(\mathcal {G}\) and the descriptions of the domain \(\mathcal {D}\) and the range \(\mathcal {R}\).
 ::
::-
This is the deterministic evaluation algorithm that takes a public parameter \(\mathsf {pp}\) and an element \(x \in \mathcal {D}\) as input, and outputs an element \(y \in \mathcal {R}\).
When there is no confusion, we will abuse the notation and denote by “\(\mathsf {CIH}(\mathsf {pp}, x)\)” to mean the execution of \(\mathsf {Eval}(\mathsf {pp}, x)\). Furthermore, when \(\mathsf {pp}\) is clear from the context, we may sometimes drop \(\mathsf {pp}\) from the input of \(\mathsf {CIH}\), and treat as if it is a single function (e.g. “\(\mathsf {CIH}: \mathcal {D}\rightarrow \mathcal {R}\)”) for more intuitive descriptions.
Security of CIHs. The security definition of a CIH that we use in this paper is a slightly generalized version of correlated-input pseudorandomness [30] (see Remark 4 for the differences from related works).
Let \(\mathsf {GGen}\) be a group generator, and \(\mathsf {CIH}= (\mathsf {PrmGen},\mathsf {Eval})\) be a publicly parameterized function with respect to \(\mathsf {GGen}\). Let \(\mathcal {F}= \{\mathcal {F}_{\lambda ,z}\}_{\lambda \in \mathbb {N},z \in \{0,1\}^*}\) be a class of functions, where each \(\mathcal {F}_{\lambda ,z}\) is a set of functions parameterized by \(\lambda \in \mathbb {N}\) and \(z \in \{0,1\}^*\),Footnote 17 and it is required that for all \(\lambda \in \mathbb {N}\), if \(\mathcal {G}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {GGen}(1^{\lambda })\) and \(\mathsf {pp}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {PrmGen}(\mathcal {G})\), then the domain and the range of functions in \(\mathcal {F}_{\lambda ,\mathsf {pp}}\) are identical to the domain of \(\mathsf {Eval}(\mathsf {pp}, \cdot )\).
For the publicly parameterized function \(\mathsf {CIH}\), the group generator \(\mathsf {GGen}\), the function class \(\mathcal {F}\), and an adversary \(\mathcal {A}\), we define the security experiment \(\mathsf {Expt}^{\mathsf {cih}}_{\mathsf {CIH},\mathcal {F},\mathcal {A}}(\lambda )\) as described in Fig. 2.
Note that in the experiment, the oracle \(\mathcal {O}(\cdot )\) that \(\mathcal {A}\) has access to, takes \(f \in \mathcal {F}_{\lambda ,\mathsf {pp}}\) as input, and returns either the evaluation result \(\mathsf {CIH}(\mathsf {pp}, f(x))\) or the output \(\mathsf {RF}(f(x))\) of the random function \(\mathsf {RF}\), depending on the challenge bit \(\mathsf {coin}\in \{0,1\}\).
Definition 2
(Security of CIH). Let \(\mathsf {CIH}\) be a publicly parameterized function with respect to a group generator \(\mathsf {GGen}\), and let \(\mathcal {F}\) be a function class. We say that \(\mathsf {CIH}\) is a CIH for \(\mathcal {F}\) (or, \(\mathcal {F}\)-CIH) with respect to \(\mathsf {GGen}\), if for all PPT adversaries \(\mathcal {A}\), the advantage \(\mathsf {Adv}_{\mathsf {CIH},\mathsf {GGen},\mathcal {F},\mathcal {A}}^{\mathsf {cih}}(\lambda ) := 2 \cdot |\Pr [\mathsf {Expt}_{\mathsf {CIH},\mathsf {GGen},\mathcal {F},\mathcal {A}}^{\mathsf {cih}}(\lambda ) = 1] - 1/2|\) is negligible.
Remark 4
(On the difference between CIHs and related-key secure PRFs (or PRGs)). This remark provides additional information for readers who are familiar with related primitives. We note that Definition 2 is essentially the same as the definition of a related-key secure pseudorandom generator (RKA-PRG) by Bellare and Cash [5, Sect. 6, Eq. (27)]. A very minor difference is that we explicitly consider public parameters in the syntax. An RKA-PRG can be seen as a generalized version of correlated-input pseudorandomness by Goyal, O’Neill, and Rao [30, Definition 7]. If \(\mathcal {A}\) in the security of a CIH must declare functions that will be queried to the oracle at the beginning of the experiment (i.e., selective security) and \(\mathsf {RF}(f(x))\) is replaced by a uniformly random element in  , then it is the same as correlated-input pseudorandomness. The reason why we select the name “CIH” is that it is well-suited for our usage.
, then it is the same as correlated-input pseudorandomness. The reason why we select the name “CIH” is that it is well-suited for our usage.
Moreover, an RKA-PRF implies an RKA-PRGFootnote 18. Therefore, the RKA-PRF (or RKA-PRG) by Bellare and Cash [5, Theorem 4.2] and the RKA-PRF by Abdalla, Benhamouda, Passelègue, and Paterson [1, Theorem 7] are secure CIHs under our definition. (Of course, supported function classes are the same as theirs.)
In Sects. 3 and 5, we introduce two concrete function classes for CIHs used as building blocks in our proposed CPRFs.
3 Building Block: Correlated-Input Secure Hash
In this section, we construct a CIH for group-induced functions on \(\mathbb {QR}_q^n\), Its security under the DDH assumption is proven in the full version [3]. The definition of group-induced functions is given below.
Quadratic Residuosity groups. A safe prime q is a prime such that \(q=2p+1\) for some p which is also a prime. We denote by \(\mathbb {QR}_q\) the subgroup of all quadratic residues in \(\mathbb {Z}_q^*\). From an elementary result, we have that \(\mathbb {QR}_q\) is a group of prime order p. We denote by \(\mathsf {SPGGen}(1^\lambda )\) a group generator that outputs a group description \((\mathbb {G}, q)\) where q is a safe prime and \(q=\varOmega (2^\lambda )\).
CIH for group-induced functions. The notion of (component-wise) group-induced functions with respect to a group generator \(\mathsf {GGen}\) is a function class \(\varPsi ^{\mathsf {g}\text {-}\mathsf {indc}}= \{ \varPsi ^{\mathsf {g}\text {-}\mathsf {indc}}_{\lambda ,z} \}_{\lambda \in \mathbb {N}, z \in \{0,1\}^*}\) satisfying the following property for all \((\lambda , z) \in \mathbb {N}\times \{0,1\}^*\): If z can be parsed as a tuple \((\mathcal {G}, n, z')\) so that \(\mathcal {G}= (\mathbb {G},q)\) is a group description output by \(\mathsf {GGen}(1^{\lambda })\), \(n \in \mathbb {N}\), and \(z' \in \{0,1\}^*\), then we have \(\varPsi ^{\mathsf {g}\text {-}\mathsf {indc}}_{\lambda ,z} = \{\psi _{\vec {a}} : (\mathbb {Z}_q^*)^n \rightarrow (\mathbb {Z}_q^*)^n \mid \vec {a} \in (\mathbb {Z}_q^*)^n\}\), where for each \(\vec {a} \in (\mathbb {Z}_q^*)^n\),  and \(\star \) denotes the component-wise multiplication in \(\mathbb {Z}^*_q\).
and \(\star \) denotes the component-wise multiplication in \(\mathbb {Z}^*_q\).
Naor-Reingold PRF. We recall the Naor-Reingold PRF [36] denoted by \(\mathsf {NR}\). The setup takes \(1^{\lambda }\) as input and outputs \(\mathsf {pp}=(\mathbb {G},g,n)\) where \(\mathbb {G}\) is a group of prime order q output from \(\mathsf {GGen}(1^\lambda )\). The key \(\mathsf {msk}= \{ x_i \}^{n}_{i=0}\) is chosen as \(x_i\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}^*_q\), and the evaluation of the function on input \((u_1,\ldots ,u_n)\in \{0,1\}^n\) is defined as  . Our PRF used in our CIH, denoted by \(\mathsf {NR}'\), is a variant of \(\mathsf {NR}\). \(\mathsf {NR}'\) is defined as \(\mathsf {NR}\), except that \(\mathsf {msk}= \{ x_i \}^{n}_{i=0}\) is chosen as \(x_i \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {QR}_q\), instead of \(x_i\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}^*_q\). In particular, the function evaluation of \(\mathsf {NR}'\) matches \(\mathsf {NR}\), but its domain is restricted to \(\mathbb {QR}_q^{n+1}\times \{0,1\}^n\).
. Our PRF used in our CIH, denoted by \(\mathsf {NR}'\), is a variant of \(\mathsf {NR}\). \(\mathsf {NR}'\) is defined as \(\mathsf {NR}\), except that \(\mathsf {msk}= \{ x_i \}^{n}_{i=0}\) is chosen as \(x_i \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {QR}_q\), instead of \(x_i\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}^*_q\). In particular, the function evaluation of \(\mathsf {NR}'\) matches \(\mathsf {NR}\), but its domain is restricted to \(\mathbb {QR}_q^{n+1}\times \{0,1\}^n\).
CIH Construction. We are now ready to describe our CIH for the (component-wise) group-induced functions with respect to \(\mathsf {SPGGen}\). It can be considered as a variant of the hash function by Bellare and Cash [5], denoted as \(\mathsf {CIH}_\mathsf {BC} \), which we recall as follows. The public parameter consists of the description of \(\mathbb {G}\), which is a cyclic group of order q, output from the group generator \(\mathsf {GGen}(1^\lambda )\), a generator g of \(\mathbb {G}\), and a collision-resistant hash function \(\mathsf {H}_{\mathsf {cr}}:\mathbb {G}^{n+1} \rightarrow \{0,1\}^{n-2}\). The evaluation is defined as follows.
The function is \(\mathsf {CIH}_\mathsf {BC} : (\mathbb {Z}_q^*)^{n+1} \longrightarrow \mathbb {G}\) and

where \(e_0=0^n\) and \(e_k=0^{k-1} \Vert 1 \Vert 0^{n-k}\) for \(k\in [n]\).
Our variant of CIH is exactly the same as \(\mathsf {CIH}_\mathsf {BC} \) but the domain is restricted. In more detail, our CIH is operated on \(\mathbb {QR}_q^{n+1} \rightarrow \mathbb {G}\) with exactly the same evaluation as \(\mathsf {CIH}_\mathsf {BC} \). Note that due to our restriction on the domain, the \(\mathsf {NR}\) evaluation inside the function is thus restricted to \(\mathsf {NR}'\). We denote this CIH as \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} \).
Theorem 1
If the DDH assumption holds with respect to \(\mathsf {SPGGen}\) and \(\mathsf {H}_{\mathsf {cr}}\) is a CRHF, then \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} \) is a secure CIH for the (component-wise) group-induced functions with respect to \(\mathsf {SPGGen}\).
4 CPRF for \({\mathbf {NC}}^1\) Circuits
In this section, we first show a construction of a CPRF for \({\mathbf {NC}}^1\) circuits with no-evaluation security, where an adversary is not allowed to make evaluation queries (Sect. 4.1). We then show that by combining the scheme with our CIH in Sect. 3, we can upgrade the security to the selective single-key security, where the adversary is allowed to make evaluation queries unbounded times after it is given the secret key (Sect. 4.2). We also show that the adaptive security can be achieved in the random oracle model in the full version [3].
4.1 Our Basic Constrained PRF
Here, we give a construction of a CPRF for \({\mathbf {NC}}^1\) with no-evaluation security. We then prove that the scheme has additional properties that we call semi-evaluability and universality. These properties will be used in security proofs of our selectively/adaptively secure CPRF for \({\mathbf {NC}}^1\) in the standard/random-oracle model. Notations. In the following, we will sometimes abuse notation and evaluate a boolean circuit \(C(\cdot ) :\{0,1\}^\ell \rightarrow \{0,1\}\) on input \(y\in \mathbb {R}^\ell \) for some ring \(\mathbb {R}\). The evaluation is done by regarding \(C(\cdot )\) as the arithmetic circuit whose AND gates \( (y_1,y_2) \mapsto y_1 \wedge y_2 \) being changed to the multiplication gates \( (y_1,y_2) \mapsto y_1y_2 \), NOT gates \(y \mapsto \lnot y\) changed to the gates \(y \mapsto 1-y\), and the OR gates \((y_1,y_2) \mapsto y_1 \vee y_2\) changed to the gates \((y_1,y_2) \mapsto y_1 + y_2 - y_1y_2\). It is easy to observe that if the input is confined within \(\{0,1\}^{\ell } \subseteq \mathbb {R}\), the evaluation of the arithmetized version of \(C(\cdot )\) equals to that of the binary version. (Here, we identify ring elements \(0,1\in \mathbb {R}\) with the binary bit.) In that way, we can regard \(C(\cdot )\) as an \(\ell \)-variate polynomial over \(\mathbb {R}\). The degree of \(C(\cdot )\) is defined as the maximum of the total degree of all the polynomials that appear during the computation.
Class of Functions. Let \(n=\mathrm {poly}(\lambda )\), \(z(n)=\mathrm {poly}(n)\), and \(d(n)=O(\log n)\) be parameters. The function class that will be dealt with by the scheme is denoted by  , where
, where  consists of (Boolean) circuits f whose input size is \(n(\lambda )\), the description size is z(n) , and the depth is d(n) . We can set the parameters arbitrarily large as long as they do not violate the asymptotic bounds above, and thus the function class corresponds to
consists of (Boolean) circuits f whose input size is \(n(\lambda )\), the description size is z(n) , and the depth is d(n) . We can set the parameters arbitrarily large as long as they do not violate the asymptotic bounds above, and thus the function class corresponds to  circuits with bounded size. The following lemma will be helpful when describing our scheme.
circuits with bounded size. The following lemma will be helpful when describing our scheme.
Lemma 1
Let \(n=\mathrm {poly}(\lambda )\). There exists a family of universal circuit \(\{ U_{n} \}_{n\in \mathbb {N}}\) of degree \(D(\lambda ) = \mathrm {poly}(\lambda )\) such that \(U_{n}(f,x)=f(x)\) for any  and \(x\in \{0,1\}^n\).
and \(x\in \{0,1\}^n\).
Proof
Due to the result by Cook and Hoover [20], there exists a universal circuit \(U_{n}(\cdot )\) of depth \(O(d)=O(\log n)\) and size \(\mathrm {poly}(n,z,d) = \mathrm {poly}(\lambda )\). Furthermore, the degree of \(U_{n}(\cdot )\) is bounded by \(2^{O(d)} = \mathrm {poly}(n)=\mathrm {poly}(\lambda )\). \(\blacksquare \)
Construction. Let  be the family of the circuit defined as above and \(\{ U_{n} \}_{n\in \mathbb {N}}\) be the family of the universal circuit defined in Lemma 1. Let the parameter \(D(\lambda )\) be the degree of the universal circuit (chosen as specified in Lemma 1). Since we will fix n in the construction, we drop the subscripts and just denote
be the family of the circuit defined as above and \(\{ U_{n} \}_{n\in \mathbb {N}}\) be the family of the universal circuit defined in Lemma 1. Let the parameter \(D(\lambda )\) be the degree of the universal circuit (chosen as specified in Lemma 1). Since we will fix n in the construction, we drop the subscripts and just denote  and U in the following. We also let \(\mathsf {HGen}\) be any group generator. The description of our CPRF \(\mathsf {CPRF}_\mathsf {NE}= (\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Eval}, \mathsf {Constrain}, \mathsf {CEval})\) is given below.
and U in the following. We also let \(\mathsf {HGen}\) be any group generator. The description of our CPRF \(\mathsf {CPRF}_\mathsf {NE}= (\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Eval}, \mathsf {Constrain}, \mathsf {CEval})\) is given below.
- \(\mathsf {Setup}(1^\lambda )\)::
-
It obtains the group description \(\mathcal {H}= ( \mathbb {H}, p)\) by running \(\mathcal {H}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {HGen}(1^\lambda )\). It then outputs the public parameter \(\mathsf {pp}:= \mathcal {H}\).Footnote 19
- \(\mathsf {KeyGen}(\mathsf {pp})\)::
-
It chooses \((b_1,...,b_z) \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_p^{z}\), \(\alpha \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_p^*\), and \(g,h_1,\ldots , h_n \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {H}\). Then it outputs
 .
. - \(\mathsf {Eval}(\mathsf {msk},x)\)::
-
Given input \(x\in \{0,1\}^n\), it computes and outputs

- \(\mathsf {Constrain}(\mathsf {msk},f)\)::
-
It first parses \((b_1,...,b_z, \alpha , g, h_1,\ldots , h_n)\leftarrow \mathsf {msk}\). Then it sets
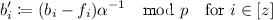
where \(f_i\) is the i-th bit of the binary representation of f. It then outputs
$$ \mathsf {sk}_f:=(f,b'_1,\ldots ,b'_z, g, g^{\alpha },\ldots ,g^{\alpha ^{D-1}}, h_1,\ldots , h_n ). $$ - \(\mathsf {CEval}(\mathsf {sk}_f,x)\)::
-
It parses \((f,b'_1,\ldots ,b'_z, g, g^{\alpha },\ldots ,g^{\alpha ^{D-1}}, h_1,\ldots , h_n ) \leftarrow \mathsf {sk}_f\). As proved in Lemma 2 below, it is possible to efficiently compute \(\{c_i\}_{i\in [D] }\) that satisfies
$$\begin{aligned} U((b_1,\ldots ,b_z),(x_1,\ldots ,x_n))= f(x) + \sum _{i=1}^{D} c_i \alpha ^i \end{aligned}$$(1)from \(\mathsf {sk}_f\) and x. If \(f(x)=0\), it computes
 and outputs X. Otherwise it outputs \(\bot \).
and outputs X. Otherwise it outputs \(\bot \).
Correctness and semi-evaluability. In order to prove the correctness, it suffices to show the following lemma.
Lemma 2
Given \(\mathsf {sk}_f\), x, one can efficiently compute \(\{c_i\}_{i\in [D] }\) satisfying Eq. (1).
Proof
The algorithm evaluates the circuit \(U(\cdot )\) on input \(( b'_1\mathsf {Z}+ f_1, \ldots , b'_z \mathsf {Z}+ f_z, x_1,\ldots , x_n )\) to obtain \(\{ c_i \}_{i \in \{ 0,1,\ldots , D \} }\) such that
where \(\mathsf {Z}\) denotes the indeterminant of the polynomial ring \(\mathbb {Z}_p[ \mathsf {Z}]\). Note that the computation is done over the ring \(\mathbb {Z}_p[ \mathsf {Z}]\) and can be efficiently performed, since we have \(D = \mathrm {poly}( \lambda )\). We prove that \(\{ c_i \}_{i\in [D]}\) actually satisfies Eq. (1). To see this, we first observe that by setting \(\mathsf {Z}= 0\) in Eq. (2), we obtain \(c_0 = U(f_1,\ldots , f_z, x_1\ldots , x_n) = f(x)\). To conclude, we further observe that by setting \(\mathsf {Z}= \alpha \) in Eq. (2), we recover Eq. (1), since we have \(b_j = b'_j \alpha + f_j\) by the definition of \(b'_j\). This completes the proof of the lemma. \(\blacksquare \)
The lemma implies an additional property of the CPRF that we call semi-evaluability, which will be useful in our security proof. We formally state it in the following lemma:
Lemma 3
There exist deterministic and efficient algorithms \(\mathsf {SEval}\) and \(\mathsf {Aux}\) satisfying the following property. For all \({\mathcal {F}}^{{{\varvec{NC}}}^1}\) and x such that \(f(x)=1\) and for all possible \(\mathsf {msk}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {KeyGen}( \mathsf {pp}), \mathsf {sk}_f\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {Constrain}(\mathsf {msk},f)\), we have
where “\(\cdot \)” indicates the group operation on \(\mathbb {H}\). (We refer to this property of our CPRF as semi-evaluability.)
Proof
We define \(\mathsf {SEval}\) and \(\mathsf {Aux}\) as follows.
- \(\mathsf {SEval}(\mathsf {sk}_f,x)\)::
-
It first parses \((f,b'_1,\ldots ,b'_z, g, g^{\alpha },\ldots ,g^{\alpha ^{D-1}}, h_1,\ldots , h_n )\leftarrow \mathsf {sk}_f\). It then compute \(\{c_j\}_{j\in [D] }\) that satisfies Eq. (1). It finally computes
 and outputs \(X'\).
and outputs \(X'\). - \(\mathsf {Aux}(\mathsf {msk})\)::
-
It parses \((b_1,\ldots ,b_z, \alpha , g, h_1,\ldots , h_n) \leftarrow \mathsf {msk}\) and outputs \(g^{1/\alpha }\).
The lemma readily follows from Eq. (1) and \(f(x)=1\). \(\blacksquare \)
Universality. The following lemma indicates that the above scheme can be seen as a universal hashing. The only reason why we need \(h_1,\ldots , h_n\) in \(\mathsf {pp}\) is to ensure this property. Formally, we have the following lemma. The lemma will be used later in this section.
Lemma 4
For all \(x, x'\in \{0,1\}^n\) with \(x\ne x'\) and \(\mathsf {pp}\) output by \(\mathsf {Setup}(1^\lambda )\), we have
\(\Pr _{}[ ~ \mathsf {msk}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {KeyGen}(\mathsf {pp}) ~ : ~ \mathsf {Eval}(\mathsf {msk}, x) = \mathsf {Eval}(\mathsf {msk}, x') ~ ] = \frac{1}{p}\).
Proof
Since \(x\ne x'\), there exists an index i such that \(x_i \ne x'_{i}\). Let us fix \(\mathsf {msk}\) except for \(h_i\). Then, we can see that there exists a unique \(h_i\) such that \(\mathsf {Eval}(\mathsf {msk}, x) = \mathsf {Eval}(\mathsf {msk}, x')\) holds. Since \(h_i\) is chosen uniformly at random from \(\mathbb {H}\), the lemma follows. \(\blacksquare \)
No-evaluation security.
Theorem 2
If the \((D-1)\)-DDHI assumption holds with respect to \(\mathsf {HGen}\), then \(\mathsf {CPRF}_\mathsf {NE}\) defined above satisfies no-evaluation security as a CPRF for the circuit class  .
.
Proof
Let \(\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)\) be any no-evaluation adversary that attacks the no-evaluation security of \(\mathsf {CPRF}\). We prove the above theorem by considering the following sequence of games.
- \(\mathsf {Game}~0\)::
-
This is the real single-key security experiment
 against the no-evaluation adversary \(\mathcal {A}=(\mathcal {A}_1,\mathcal {A}_2)\). Namely,
against the no-evaluation adversary \(\mathcal {A}=(\mathcal {A}_1,\mathcal {A}_2)\). Namely,

- \(\mathsf {Game}~1\)::
-
In this game, we change the way \(\mathsf {sk}_f\) is sampled. In particular, we change the way of choosing \(\{b_i\}_{i\in [z]}\) and \(\{b'_i\}_{i\in [z]}\). Namely, given the constraining query f from \(\mathcal {A}_1\), the game picks \((b'_1,\ldots ,b'_z)\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_p^{z}\), \(\alpha \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_p^*\), and sets \(b_i:=b'_i \alpha + f_i \mod p\) for \(i \in [z]\).
- \(\mathsf {Game}~2\) :
-
In this game, we change the challenge oracle \(\mathcal {O}_{\mathsf {Chal}}( \cdot )\) as follows:
- \(\mathcal {O}_{\mathsf {Chal}}(x^*)\)::
-
Given \(x^* \in \{0,1\}^n\) as input, it returns \(\mathsf {SEval}(\mathsf {sk}_f,x^*)\cdot \mathsf {Aux}(\mathsf {msk})\) if \(\mathsf {coin}=1\) and \(X^*\) if \(\mathsf {coin}= 0\).
- \(\mathsf {Game}~3\)::
-
In this game, we further change the challenge oracle as follows:
- \(\mathcal {O}_{\mathsf {Chal}}(x^*)\)::
-
Given \(x^* \in \{0,1\}^n\) as input, it first picks \(\psi \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {H}\) and returns \( \mathsf {SEval}(\mathsf {sk}_f,x) \cdot \psi \) if \(\mathsf {coin}=1\) and \(X^*\) if \(\mathsf {coin}= 0\).
- \(\mathsf {Game}~4\) :
-
In this game, the oracle is changed as follows.
- \(\mathcal {O}_{\mathsf {Chal}}(x^*)\)::
-
Given \(x^* \in \{0,1\}^n\) as input, it returns \(X^*\) regardless of the value of \(\mathsf {coin}\).
Let \(\mathsf {T}_i\) be the event that \(\mathsf {Game}~i\) returns 1.
Lemma 5
It holds that \(\Pr [\mathsf {T}_1]=\Pr [\mathsf {T}_0]\), \(\Pr [\mathsf {T}_2]=\Pr [\mathsf {T}_1]\), \(\Pr [\mathsf {T}_3]=\Pr [\mathsf {T}_4]\), and \(|\Pr [\mathsf {T}_4]-1/2|=0\).
Lemma 6
If the \((D-1)\)-DDHI assumption holds, then \(|\Pr [\mathsf {T}_3]-\Pr [\mathsf {T}_2]|=\mathrm {negl}(\lambda )\).
Therefore, the advantage of \(\mathcal {A}\) is  . See the full version for proofs of these lemmas. \(\blacksquare \)
. See the full version for proofs of these lemmas. \(\blacksquare \)
4.2 Selectively-Secure CPRF in the Standard Model
Here, we give our CPRF for  with selectively single-key security in the standard model. The scheme is obtained by combining our CPRF \(\mathsf {CPRF}_\mathsf {NE}= (\mathsf {Setup}_\mathsf {NE}, \mathsf {KeyGen}_{\mathsf {NE}}, \mathsf {Eval}_{\mathsf {NE}}, \mathsf {Constrain}_{\mathsf {NE}}, \mathsf {CEval}_{\mathsf {NE}})\) for the function class
with selectively single-key security in the standard model. The scheme is obtained by combining our CPRF \(\mathsf {CPRF}_\mathsf {NE}= (\mathsf {Setup}_\mathsf {NE}, \mathsf {KeyGen}_{\mathsf {NE}}, \mathsf {Eval}_{\mathsf {NE}}, \mathsf {Constrain}_{\mathsf {NE}}, \mathsf {CEval}_{\mathsf {NE}})\) for the function class  in Sect. 4.1 with our CIH \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} = (\mathsf {PrmGen}_{\widetilde{\mathsf {BC} }}, \mathsf {Eval}_{\widetilde{\mathsf {BC} }})\) constructed in Sect. 3. For the simplicity of the notation, we will denote \(\mathsf {Eval}_{\widetilde{\mathsf {BC} }}(\mathsf {pp}_\mathsf {CIH}, \cdot )\) by \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} (\cdot )\) when \(\mathsf {pp}_\mathsf {CIH}\) is clear. Let \(\mathsf {SPGGen}\) denote the group generator defined in Sect. 3. The construction of our scheme
in Sect. 4.1 with our CIH \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} = (\mathsf {PrmGen}_{\widetilde{\mathsf {BC} }}, \mathsf {Eval}_{\widetilde{\mathsf {BC} }})\) constructed in Sect. 3. For the simplicity of the notation, we will denote \(\mathsf {Eval}_{\widetilde{\mathsf {BC} }}(\mathsf {pp}_\mathsf {CIH}, \cdot )\) by \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} (\cdot )\) when \(\mathsf {pp}_\mathsf {CIH}\) is clear. Let \(\mathsf {SPGGen}\) denote the group generator defined in Sect. 3. The construction of our scheme  is as follows:
is as follows:
- \(\mathsf {Setup}(1^{\lambda })\)::
-
It first runs \(\mathcal {G}_0 \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {SPGGen}(1^\lambda )\) to obtain the group description \(\mathcal {G}_0 := (\mathbb {G}, q )\). Recall that \(\mathcal {G}_0\) also defines the description of the group \(\mathbb {QR}_q \subset \mathbb {Z}_q^*\) of prime order \(p= (q-1)/2\). We denote the description of the group by \(\mathcal {G}_1:=( \mathbb {QR}_q, p)\). It then samples \(\mathsf {pp}_\mathsf {CIH}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {PrmGen}_{\widetilde{\mathsf {BC} }}(\mathcal {G}_0)\). Let
 . It outputs
. It outputs  .
. - \(\mathsf {KeyGen}(\mathsf {pp})\)::
-
It first parses \((\mathsf {pp}_\mathsf {CIH}, \mathsf {pp}_{\mathsf {NE}}) \leftarrow \mathsf {pp}\) and runs \(\mathsf {msk}_i \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {KeyGen}_{\mathsf {NE}}(\mathsf {pp}_\mathsf {NE})\) for \(i\in [m]\). It then outputs
 .
. - \(\mathsf {Eval}(\mathsf {msk}, x)\)::
-
It first parses \((\mathsf {msk}_1,...,\mathsf {msk}_m)\leftarrow \mathsf {msk}\) and outputs

where we recall that we have \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} : (\mathbb {QR}_q)^m \rightarrow \mathbb {G}\) and \(\mathsf {Eval}_{\mathsf {NE}}(\mathsf {msk}_i, \cdot ): \{0,1\}^n \rightarrow \mathbb {QR}_q\) for \(i\in [m]\) (for simplicity, we omit writing \(\mathsf {pp}_\mathsf {CIH}\) and \(\mathsf {pp}_\mathsf {NE}\) here).
- \(\mathsf {Constrain}(\mathsf {msk},f)\)::
-
It first parses \((\mathsf {msk}_1,...,\mathsf {msk}_m)\leftarrow \mathsf {msk}\). It then computes \(\mathsf {sk}_{f,i}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {Constrain}_{\mathsf {NE}}(\mathsf {msk}_i,f)\) for \(i\in [m]\) and outputs
 .
. - \(\mathsf {CEval}(\mathsf {sk}_f,x)\)::
-
It first parses \((\mathsf {sk}_{f,1},...,\mathsf {sk}_{f,m})\leftarrow \mathsf {sk}_f\). It then computes
 for \(i\in [m]\) and outputs \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} (X_1,...,X_m)\).
for \(i\in [m]\) and outputs \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} (X_1,...,X_m)\).
Remark 5
In the above, we need m instances of \(\mathsf {CPRF}_\mathsf {NE}\), which may seem redundant. This is necessary because the domain of the CIH constructed in Sect. 3 is \(\mathbb {QR}^m\) for \(m=poly(\lambda )\), and thus input of the CIH must be an m-dimensional vector. If we had a CIH for group-induced function on \(\mathbb {QR}\), then the m times blowup could be avoided.
Remark 6
The algorithm \(\mathsf {Setup}\) implicitly uses the group generator \(\mathsf {SPGGen}'\) that first runs \(\mathsf {SPGGen}\) to obtain \(\mathcal {G}=(\mathbb {G},q)\) and then outputs the group description \((\mathbb {QR}_q, p)\). Here, from the technical reason, we assume that the description of \(\mathbb {QR}_q\) implicitly contains that of \(\mathbb {G}\) as well. While our construction in Sect. 4.1 can be instantiated with any prime-order group generator \(\mathsf {HGen}\), our scheme above requires to instantiate the scheme with the specific group generator \(\mathsf {SPGGen}'\).
It is easy to observe that the correctness of the above scheme follows from that of the underlying schemes. The following theorem addresses the security of the scheme.
Theorem 3
The above construction  is a selective single-key secure CPRF for the function class
is a selective single-key secure CPRF for the function class  if the \((D-1)\)-DDHI assumption holds with respect to \(\mathsf {SPGGen}'\) (see Remark 6) and the DDH assumption holds with respect to \(\mathsf {SPGGen}\).
if the \((D-1)\)-DDHI assumption holds with respect to \(\mathsf {SPGGen}'\) (see Remark 6) and the DDH assumption holds with respect to \(\mathsf {SPGGen}\).
Proof
The security of the scheme will be proven by the no-evaluation security, semi-evaluability, and universality of \(\mathsf {CPRF}_\mathsf {NE}\) as well as correlated-input security of \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} \) for (component-wise) group-induced functions. Let \(\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)\) be any selectively admissible adversary that attacks the selective single-key security of \(\mathsf {CPRF}\). For simplicity, we assume that \(\mathcal {A}_2\) never makes the same query twice, makes a challenge query only once (see Remark 2), and all evaluation queries x made by \(\mathcal {A}_2\) satisfy \(f(x) = 1\). In the following, Q denotes the upper bound on the number of the access to the evaluation oracle \(\mathsf {Eval}(\mathsf {msk}, \cdot )\) made by \(\mathcal {A}_2\). We prove the theorem by considering the following sequence of games.
- \(\mathsf {Game}~0\)::
-
This is the actual single-key security experiment
 (\(\lambda \)) against the selective adversary \(\mathcal {A}=(\mathcal {A}_1,\mathcal {A}_2)\) where the coin of the game is fixed to \( \mathsf {coin}= 1\). Namely,
(\(\lambda \)) against the selective adversary \(\mathcal {A}=(\mathcal {A}_1,\mathcal {A}_2)\) where the coin of the game is fixed to \( \mathsf {coin}= 1\). Namely,

- \(\mathsf {Game}~1\)::
-
In this game, we do not differentiate the challenge oracle \(\mathcal {O}_\mathsf {Chal}(\cdot )\) from \(\mathsf {Eval}(\mathsf {msk}, \cdot )\) and identify them. Namely, \(\mathcal {A}_2\) is equipped with the following oracle \(\mathcal {O}_{\mathsf {Merge}}(\cdot )\) defined below, instead of \(\mathcal {O}_\mathsf {Chal}(\cdot )\) and \(\mathsf {Eval}(\mathsf {msk}, \cdot )\):
- \(\mathcal {O}_{\mathsf {Merge}}(\cdot )\)::
-
Given the j-th query \(x^{(j)} \in \{0,1\}^{n}\) from \(\mathcal {A}_2\), the oracle first computes
 for \(i\in [m]\), and then returns
for \(i\in [m]\), and then returns  .
.
(We note that \(\mathcal {O}_{\mathsf {Merge}}(\cdot )\) simply returns \(\mathsf {Eval}(\mathsf {msk},x)\) given x.) Since we do not differentiate the challenge query \(x^*\) from the evaluation queries in this game, we have \(x^{*} = x^{(j)}\) for some \(j \in [Q+1]\).
- \(\mathsf {Game}~2\)::
-
Let \(\mathsf {Col}\) be the event that there exist \(j_1\ne j_2 \in [Q+1]\) such that \((X_1^{(j_1)},\ldots , X_m^{(j_1)})= (X_1^{(j_2)},\ldots , X_m^{(j_2)})\). If \(\mathsf {Col}\) occurs, the game immediately aborts and outputs a uniformly random bit. The rest is the same as the previous game.
- \(\mathsf {Game}~3\) :
-
In this game, we change the way \(\{X_i^{(j)}\}_{ i\in [m], j\in [Q+1]}\) is created. In particular, \(\mathcal {O}_{\mathsf {Merge}}(\cdot )\) works as follows:
- \(\mathcal {O}_{\mathsf {Merge}}(\cdot )\)::
-
Given the j-th query \(x^{(j)} \in \{0,1\}^{n}\) from \(\mathcal {A}_2\), it proceeds as follows.
There are two cases to consider:
-
1.
For the first query \(x^{(1)}\), it first computes

Then, it computes and returns
 .
. -
2.
To answer queries \(x^{(j)}\) with \(j>1\), it first computes
 (3)
(3)for \(i\in [m]\). Then it computes and returns
 .
.
Note that during the above phase, as soon as the game finds \(j_1\ne j_2 \in [Q+1]\) such that \((X_1^{(j_1)},\ldots , X_m^{(j_1)})= (X_1^{(j_2)},\ldots , X_m^{(j_2)})\), the game aborts and outputs a random bit (as specified in \(\mathsf {Game}~2\)).
- \(\mathsf {Game}~4\) :
-
We define \(\mathsf {Col}'\) as the event that there exist \(j_1\ne j_2 \in [Q+1]\) such that
$$ \mathsf {SEval}_{\mathsf {NE}}(\mathsf {sk}_{f ,i }, x^{(j_1)}) = \mathsf {SEval}_{\mathsf {NE}}(\mathsf {sk}_{f,i}, x^{(j_2)}) \quad \forall i \in [m] . $$In this game, the game aborts when \(\mathsf {Col}'\) occurs instead of \(\mathsf {Col}\).
- \(\mathsf {Game}~5\)::
-
In this game, we change the way \(X^{(1)}_i\) is chosen. In particular, the first item of the description of the oracle \(\mathcal {O}_{\mathsf {Merge}}(\cdot )\) in \(\mathsf {Game}~3\) is changed as follows:
-
1.
For the first query \(x^{(1)}\), the oracle sets
$$ X^{(1)}_i\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {QR}_q \quad \text{ for } i\in [m]. $$Then, it computes and returns
 .
.
- \(\mathsf {Game}~6\) :
-
In this game, we further change the oracle \(\mathcal {O}_{\mathsf {Merge}}(\cdot )\) as follows:
- \(\mathcal {O}_{\mathsf {Merge}}(\cdot )\)::
-
Given the j-th query \(x^{(j)} \in \{0,1\}^{n}\) from \(\mathcal {A}_2\), it picks \(y^{(j)}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {G}\) and returns it.
- \(\mathsf {Game}~7\) :
-
This is the real game with the coin being fixed to \(\mathsf {coin}= 0\). Namely, \(\mathcal {A}_2\) is equipped with the oracles \(\mathcal {O}_\mathsf {Chal}(\cdot )\) and \(\mathsf {Eval}(\mathsf {msk}, \cdot )\) that work as follows. (We do not consider \(\mathcal {O}_{\mathsf {Merge}}(\cdot )\) any more.)
- \(\mathsf {Eval}(\mathsf {msk}, \cdot ):\) :
-
Given \(x\in \{0,1\}^{n}\) as input, it returns \(\mathsf {Eval}( \mathsf {msk}, x )\).
- \(\mathcal {O}_{\mathsf {Chal}}(\cdot )\)::
-
Given \(x^* \in \{0,1\}^n\) as input, it picks \(y^* \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {G}\) and returns it. (Recall that we set \(\mathsf {coin}=0\) in this game.)
Let \(\mathsf {T}_i\) be the event that \(\mathsf {Game}~i\) returns 1.
Lemma 7
\(\Pr [\mathsf {T}_1]=\Pr [\mathsf {T}_0]\).
Proof
Since \(\mathsf {coin}=1\) in \(\mathsf {Game}~0\), we have \(\mathcal {O}_{\mathsf {Chal}}(\cdot ) = \mathsf {Eval}(\mathsf {msk}, \cdot )\). Therefore, this is only the conceptual change. \(\blacksquare \)
Lemma 8
If \(m\ge n\), \(|\Pr [\mathsf {T}_2]-\Pr [\mathsf {T}_1]| =\mathrm {negl}(\lambda )\).
See the full version [3] for the proof of this lemma. This is proved by the union bound and the universality of \(\mathsf {CPRF}_\mathsf {NE}\) (Lemma 4).
Lemma 9
\(\Pr [\mathsf {T}_3]=\Pr [\mathsf {T}_2].\)
Proof
We prove that the change is only conceptual. The difference between the games is that \(X_i^{(j)}\) is computed as \(\mathsf {Eval}_{\mathsf {NE}}(\mathsf {msk}_i,x^{(j)})\) in \(\mathsf {Game}~2\), whereas it is computed as the right-hand side of Eq. (3) in \(\mathsf {Game}~3\). We show here that they are actually equivalent. The right-hand side of Eq. (3) equals to
where we used our simplification assumption that \(f(x^{ (1) })=f(x^{(j)})=1\) and semi-evaluability (Lemma 3) in the first and the last equations above. \(\blacksquare \)
Lemma 10
\(\Pr [\mathsf {T}_4] = \Pr [\mathsf {T}_3].\)
Proof
It suffices to show that the abort conditions \(\mathsf {Col}\) and \(\mathsf {Col}'\) are equivalent. We have
Hence, the change is only conceptual. The lemma readily follows. \(\blacksquare \)
Lemma 11
If \(\mathsf {CPRF}_\mathsf {NE}\) satisfies no-evaluation security when instantiated by the group generator  , we have \(|\Pr [\mathsf {T}_5]-\Pr [\mathsf {T}_4]|=\mathrm {negl}(\lambda )\).
, we have \(|\Pr [\mathsf {T}_5]-\Pr [\mathsf {T}_4]|=\mathrm {negl}(\lambda )\).
Proof
For the sake of the contradiction, let us assume \(|\Pr [\mathsf {T}_5]-\Pr [\mathsf {T}_4]|\) is non-negligible for the adversary \(\mathcal {A}=(\mathcal {A}_1,\mathcal {A}_2)\). We consider the following hybrid games for \(k\in \{0,1,\ldots ,m\}\):
-
\(\mathsf {Game}~4.k\): This is the same as \(\mathsf {Game}~4\) with the following difference. In this game, \(X^{(1)}_i\) is set as \(X^{(1)}_i = \mathsf {Eval}_{\mathsf {NE}}(\mathsf {msk}_i, x^{(1)}) \) when \(i> k\) and \(\tilde{X}_i \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {QR}_q\) when \(i\le k\).
By the definition, we have \(\mathsf {Game}~4.0\) (resp. \(\mathsf {Game}~4.m\)) is equivalent to \(\mathsf {Game}~4\) (resp. \(\mathsf {Game}~5\)). Therefore, we have
where \(\Pr [\mathsf {T}_i]\) denotes the probability that \(\mathsf {Game}~4.k\) outputs 1. By the above inequality, we have that there exists an index \(k^*\) such that \(|\Pr [ \mathsf {T}_{4.k^*} ] - \Pr [ \mathsf {T}_{4.{k^*-1}} ]|\) is non-negligible. We then construct an adversary \(\mathcal {B}=(\mathcal {B}_1,\mathcal {B}_2)\) that breaks the no-evaluation security of the underlying scheme \(\mathsf {CPRF}_\mathsf {NE}\). The description of \(\mathcal {B}\) is as follows.
- \(\mathcal {B}_1(\mathsf {pp}_\mathsf {NE})\)::
-
Given the group description \(\mathsf {pp}_\mathsf {NE}= (\mathbb {QR}_q, p)\), \(\mathcal {B}_1\) first recovers the group description \(\mathcal {G}_0 = (\mathbb {G}, q)\) from \( (\mathbb {QR}_q, p)\) (See remark Remark 6). \(\mathcal {B}_1\) then samples \(\mathsf {pp}_\mathsf {CIH}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {PrmGen}_{\widetilde{\mathsf {BC} }}(\mathcal {G}_0)\) and sets
 . It then runs \((f,\mathsf {st}_\mathcal {A}) \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathcal {A}_1(\mathsf {pp})\) and outputs
. It then runs \((f,\mathsf {st}_\mathcal {A}) \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathcal {A}_1(\mathsf {pp})\) and outputs  .
. - \(\mathcal {B}_2^{\mathcal {O}_{\mathsf {Chal}}(\cdot )}(\mathsf {sk}_f, \mathsf {st}_{\mathcal {B}})\)::
-
Here, we denote the master secret key of the no-evaluation security game (played for \(\mathcal {B}\)) by \(\mathsf {msk}'\). The task of \(\mathcal {B}_2\) is to distinguish whether \(\mathcal {O}_{\mathsf {Chal}}(\cdot )\) corresponds to \(\mathsf {Eval}_{\mathsf {NE}}(\mathsf {msk}',\cdot )\) or \(\mathsf {RF}(\cdot )\). First, \(\mathcal {B}_2\) picks \(\mathsf {msk}_i \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {KeyGen}_{\mathsf {NE}}(\mathsf {pp}_\mathsf {NE})\) for \(i\in \{ k^* +1, \ldots , m \} \). \(\mathcal {B}_2\) then runs \(\mathcal {A}_2(\mathsf {sk}_f, \mathsf {st}_{\mathcal {A}})\) and simulates \(\mathcal {O}_\mathsf {Merge}( \cdot )\) for \(\mathcal {A}_2\) as follows:
- −:
-
To answer the first query \(x^{(1)}\) from \(\mathcal {A}_2\), \(\mathcal {B}_2\) submits the same \(x^{(1)}\) to its challenge oracle \(\mathcal {O}_\mathsf {Chal}(\cdot )\). Then, \(\mathcal {B}_2\) is given R. Then, \(\mathcal {B}_2\) sets \(X^{(1)}_i = \mathsf {SEval}_{\mathsf {NE}}(\mathsf {msk}_i, x^{(1)})\) for \(i\ \ge k^*+1\), \(X^{(1)}_{k^*} = R\), and samples \(X^{(1)}_i \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {QR}_q\) for \(i\le k^* -1\). Finally, \(\mathcal {B}_2\) returns \(y^{(1)}= \mathsf {CIH}_{\widetilde{\mathsf {BC} }} (X^{(1)}_1,\ldots , X^{(1)}_m)\) to \(\mathcal {A}_2\).
- −:
-
To answer the query \(x^{(j)}\) with \(j>1\) from \(\mathcal {A}_2\), \(\mathcal {B}_2\) first parses \(\mathsf {sk}_f \rightarrow (\mathsf {sk}_{f,1},\ldots , \mathsf {sk}_{f,m})\) and computes
 for \(i\in [m]\). It then returns \(y^{(j)} = \mathsf {CIH}_{\widetilde{\mathsf {BC} }} (X^{(j)}_1,\ldots , X^{(j)}_m)\) to \(\mathcal {A}_2\).
for \(i\in [m]\). It then returns \(y^{(j)} = \mathsf {CIH}_{\widetilde{\mathsf {BC} }} (X^{(j)}_1,\ldots , X^{(j)}_m)\) to \(\mathcal {A}_2\).
Note that during the above phase, as soon as \(\mathcal {B}_2\) finds \(j_1\ne j_2 \in [Q]\) such that \((X_1^{(j_1)},\ldots , X_m^{(j_1)})= (X_1^{(j_2)},\ldots , X_m^{(j_2)})\), \(\mathcal {B}_2\) aborts and outputs a random bit. When \(\mathcal {A}_2\) terminates with output \(\widehat{\mathsf {coin}}\), \(\mathcal {B}_2\) outputs \(\widehat{\mathsf {coin}}\) as its guess and terminates.
The above completes the description of \(\mathcal {B}\). It is straightforward to see that \(\mathcal {B}\) makes only single challenge query. It is also easy to see that \(\mathcal {B}\) simulates \(\mathsf {Game}~4.(k^*-1)\) for \(\mathcal {A}\) when \(\mathcal {B}\)’s challenge oracle is \(\mathsf {Eval}_{\mathsf {NE}}(\mathsf {msk}',\cdot )\) and \(\mathsf {Game}~4.k^*\) when \(\mathcal {B}\)’s challenge oracle is \(\mathsf {RF}(\cdot )\). Note that in the former case, \(\mathcal {B}\) implicitly sets  . Since \(\mathcal {B}\) outputs 1 if and only if \(\mathcal {A}\) outputs 1, we have that \(\mathcal {B}\)’s advantage is \(| \Pr [\mathsf {T}_{4.k^*-1}] - \Pr [\mathsf {T}_{4.k^*}] |\), which is non-negligible. This completes the proof of the lemma. \(\blacksquare \)
. Since \(\mathcal {B}\) outputs 1 if and only if \(\mathcal {A}\) outputs 1, we have that \(\mathcal {B}\)’s advantage is \(| \Pr [\mathsf {T}_{4.k^*-1}] - \Pr [\mathsf {T}_{4.k^*}] |\), which is non-negligible. This completes the proof of the lemma. \(\blacksquare \)
Lemma 12
If \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} \) is a \(\varPsi ^{\mathsf {g}\text {-}\mathsf {indc}}\)-CIH with respect to \(\mathsf {SPGGen}\), then we have \(|\Pr [\mathsf {T}_6]-\Pr [\mathsf {T}_5]|=\mathrm {negl}(\lambda )\).
Proof
For the sake of the contradiction, let us assume that \(|\Pr [\mathsf {T}_6]-\Pr [\mathsf {T}_5]|\) is non-negligible for the adversary \(\mathcal {A}=(\mathcal {A}_1,\mathcal {A}_2)\). We then construct an adversary \(\mathcal {B}\) that breaks the security of \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} \) as follows.
- \(\mathcal {B}^{\mathcal {O}(\cdot )}( \mathsf {pp}_{\mathsf {CIH}} )\)::
-
At the beginning of the game, \(\mathcal {B}\) is given the public parameter \(\mathsf {pp}_{\mathsf {CIH}}\) of the CIH. Then it parses the group description \((\mathbb {G}, q)\) from \(\mathsf {pp}_{\mathsf {CIH}}\) and obtains the description of another group
 . It then sets
. It then sets  and runs \((f,\mathsf {st}_\mathcal {A})\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathcal {A}_1(\mathsf {pp})\). It further samples \(\mathsf {msk}_i \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {KeyGen}_{\mathsf {NE}}(\mathsf {pp}_\mathsf {NE})\) and \(\mathsf {sk}_{f,i}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {Constrain}_{\mathsf {NE}}(\mathsf {msk}_i, f)\) for \(i\in [m]\). It then gives the input \(\mathsf {sk}_f:= (\mathsf {sk}_{f,1},\ldots , \mathsf {sk}_{f,m})\) and \(\mathsf {st}_\mathcal {A}\) to \(\mathcal {A}_2\) and simulates \(\mathcal {O}_{\mathsf {Merge}}( \cdot )\) for \(\mathcal {A}_2\) as follows:
and runs \((f,\mathsf {st}_\mathcal {A})\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathcal {A}_1(\mathsf {pp})\). It further samples \(\mathsf {msk}_i \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {KeyGen}_{\mathsf {NE}}(\mathsf {pp}_\mathsf {NE})\) and \(\mathsf {sk}_{f,i}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {Constrain}_{\mathsf {NE}}(\mathsf {msk}_i, f)\) for \(i\in [m]\). It then gives the input \(\mathsf {sk}_f:= (\mathsf {sk}_{f,1},\ldots , \mathsf {sk}_{f,m})\) and \(\mathsf {st}_\mathcal {A}\) to \(\mathcal {A}_2\) and simulates \(\mathcal {O}_{\mathsf {Merge}}( \cdot )\) for \(\mathcal {A}_2\) as follows: - −:
-
To answer the first query \(x^{(1)}\) from \(\mathcal {A}_2\), \(\mathcal {B}\) queries its oracle on input
 to obtain \(y^{(1)}\). It then passes \(y^{(1)}\) to \(\mathcal {A}_2\).
to obtain \(y^{(1)}\). It then passes \(y^{(1)}\) to \(\mathcal {A}_2\). - −:
-
To answer the query \(x^{(j)}\) with \(j>1\) from \(\mathcal {A}_2\), \(\mathcal {B}\) first parses \(\mathsf {sk}_f \rightarrow \) (\(\mathsf {sk}_{f,1},\ldots , \mathsf {sk}_{f,m}\)) and computes
 (
( ) for \(i\in [m]\). \(\mathcal {B}\) then sets \(\vec {\phi }^{(j)} = (\phi _1^{(j)}, \ldots , \phi _m^{(j)})\) and queries \(\vec {\phi }^{(j)}\) to its oracle. Given the response \(y^{(j)}\) from the oracle, \(\mathcal {B}_2\) relays the same value to \(\mathcal {A}_2\).
) for \(i\in [m]\). \(\mathcal {B}\) then sets \(\vec {\phi }^{(j)} = (\phi _1^{(j)}, \ldots , \phi _m^{(j)})\) and queries \(\vec {\phi }^{(j)}\) to its oracle. Given the response \(y^{(j)}\) from the oracle, \(\mathcal {B}_2\) relays the same value to \(\mathcal {A}_2\).
Note that during the above phase, as soon as \(\mathcal {B}\) finds \(j_1\ne j_2 \in [Q]\) such that \(\mathsf {SEval}_{\mathsf {NE}}(\mathsf {sk}_{f ,i }, x^{(j_1)}) = \mathsf {SEval}_{\mathsf {NE}}(\mathsf {sk}_{f,i}, x^{(j_2)})\) for all \(i\in [m]\), it aborts and outputs a random bit. When \(\mathcal {A}_2\) terminates with output \(\widehat{\mathsf {coin}}\), \(\mathcal {B}\) outputs the same \(\widehat{\mathsf {coin}}\) and terminates.
The above completes the description of \(\mathcal {B}\). Here, we prove that \(\mathcal {B}\) simulates \(\mathsf {Game}~5\) when \(\mathcal {B}\)’s challenge coin \(\mathsf {coin}'\) is 1 and \(\mathsf {Game}~6\) when \(\mathsf {coin}'=0\).
We start by proving the former statement. When \(\mathsf {coin}'=1\), the CIH security experiment chooses randomness  during the game and the oracle \(\mathcal {O}(\cdot ) \) returns \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} (\vec {R}\star \vec {\phi } )\) on input \(\mathcal {B}\)’s query \(\vec {\phi } =(\phi _1,\ldots , \phi _m)\in \mathbb {QR}_q^m\). The view of \(\mathcal {A}_2\) corresponds to \(\mathsf {Game}~5\), with \(X^{(1)}_i\) being implicitly set as
during the game and the oracle \(\mathcal {O}(\cdot ) \) returns \(\mathsf {CIH}_{\widetilde{\mathsf {BC} }} (\vec {R}\star \vec {\phi } )\) on input \(\mathcal {B}\)’s query \(\vec {\phi } =(\phi _1,\ldots , \phi _m)\in \mathbb {QR}_q^m\). The view of \(\mathcal {A}_2\) corresponds to \(\mathsf {Game}~5\), with \(X^{(1)}_i\) being implicitly set as  for \(i\in [m]\).
for \(i\in [m]\).
We next show the latter statement. When \(\mathsf {coin}'=0\), the CIH security experiment chooses randomness  during the game and the oracle \(\mathcal {O}(\cdot ) \) returns \(\mathsf {RF}(\vec {R} \star \vec {\phi } )\) on input \(\mathcal {B}\)’s query \(\vec {\phi } =(\phi _1,\ldots , \phi _m)\) where \(\mathsf {RF}(\cdot )\) is a random function. In order to prove that \(\mathcal {B}\) simulates \(\mathsf {Game}~6\), it suffices to show that all the queries made by \(\mathcal {B}\) are distinct. We have
during the game and the oracle \(\mathcal {O}(\cdot ) \) returns \(\mathsf {RF}(\vec {R} \star \vec {\phi } )\) on input \(\mathcal {B}\)’s query \(\vec {\phi } =(\phi _1,\ldots , \phi _m)\) where \(\mathsf {RF}(\cdot )\) is a random function. In order to prove that \(\mathcal {B}\) simulates \(\mathsf {Game}~6\), it suffices to show that all the queries made by \(\mathcal {B}\) are distinct. We have
by the definition. Since \(\mathcal {B}\) aborts whenever \(\mathsf {Col}'\) occurs, this implies that \(\mathcal {B}\) does not make the same oracle query twice. \(\blacksquare \)
Lemma 13
We have \(|\Pr [T_7]-\Pr [T_6]|=\mathrm {negl}(\lambda )\).
Proof
This can be proven by applying the same game changes as that from \(\mathsf {Game}~0\) to \(\mathsf {Game}~6\) in a reverse order, with the only difference that the challenge query \(x^*\) is always returned by a uniformly random group element \(y^* \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {G}\). \(\blacksquare \)
We have

This completes the proof of the theorem. \(\blacksquare \)
5 Private Constrained PRF for Bit-Fixing
In this section, we construct a single-key private CPRF for bit-fixing. Our scheme is selectively secure under the DDH assumption. We also construct an adaptively secure single-key private CPRF for bit-fixing in the ROM in the full version [3].
Bit-fixing functions. First, we define a function class of bit-fixing functions formally. The class  of bit-fixing functions is defined as followsFootnote 20.
of bit-fixing functions is defined as followsFootnote 20.  is defined to be the set \(\{\mathsf {BF}_{c}\}_{c\in \{0,1,*\}^n}\) where
is defined to be the set \(\{\mathsf {BF}_{c}\}_{c\in \{0,1,*\}^n}\) where

By an abuse of notation, we often write c to mean \(\mathsf {BF}_c\) when the latter is given as an input to an algorithm.
CIH for affine functions. We introduce the notion of affine functions for CIH since it is used in our private CPRF for bit-fixing. The class of affine functions with respect to a group generator \(\mathsf {GGen}\), denoted by \(\varPhi ^{\mathsf {aff}}= \{\varPhi ^{\mathsf {aff}}_{\lambda ,z}\}_{\lambda \in \mathbb {N}, z \in \{0,1\}^*}\), is a function class satisfying the following property for every \((\lambda , z) \in \mathbb {N}\times \{0,1\}^*\): If z can be parsed as a tuple \((\mathcal {G}, m, z')\) so that \(\mathcal {G}= (\mathbb {G},p)\) is a group description output by \(\mathsf {GGen}(1^{\lambda })\), \(m \in \mathbb {N}\), and \(z' \in \{0,1\}^*\), then we have \(\varPhi ^{\mathsf {aff}}_{\lambda , z} = \{\phi _{\vec {u},\vec {v}} : \mathbb {Z}_p^m \rightarrow \mathbb {Z}_p^m \mid \vec {u} \in (\mathbb {Z}^*_p)^m, \vec {v} \in \mathbb {Z}^m_p\}\), where for each \(\vec {u},\vec {v}\),  and \(\odot \) denotes the component-wise multiplication in \(\mathbb {Z}_p\).
and \(\odot \) denotes the component-wise multiplication in \(\mathbb {Z}_p\).
We will use the following theorem that is implicitly proven by Abdalla et al. [1] (see also Remark 4).
Theorem 4
(implicit in [1, Theorem 7]) Let \(\mathsf {GGen}\) be a group generator. If the DDH assumption holds with respect to \(\mathsf {GGen}\), then for any polynomial \(m = m(\lambda ) \in \varOmega (\lambda )\), there exists a \(\varPhi ^{\mathsf {aff}}\)-CIH \(\mathsf {CIH}_{\mathsf {aff}} = (\mathsf {PrmGen}_{\mathsf {aff}},\mathsf {Eval}_{\mathsf {aff}})\) with respect to \(\mathsf {GGen}\), with the following property: For all \(\lambda \in \mathbb {N}\), if \(\mathcal {G}=(\mathbb {G},p) \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {GGen}(1^{\lambda })\) and \(\mathsf {pp}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {PrmGen}_{\mathsf {aff}}(\mathcal {G})\), then \(\mathsf {pp}\) can be parsed as \((\mathcal {G}, m, z')\) for some \(z' \in \{0,1\}^*\), and furthermore \(\mathsf {Eval}_{\mathsf {aff}}(\mathsf {pp}, \cdot )\) is a function with domain \(\mathbb {Z}_p^m\) and range \(\mathbb {G}\).
This theorem is derived from the following facts. (1) Abdalla et al. [1] constructed RKA-PRF for affine functions based on the DDH assumption. (2) Bellare and Cash [6] showed that RKA-PRF for a function class implies RKA-PRG for the same function class. (3) Our definition of CIH is the same as that of RKA-PRG (See Remark 4).
5.1 Construction in the Standard Model
Construction. Here, we give a construction of a selectively secure private CPRF for bit-fixing. Our CPRF is built on a \(\varPhi ^{\mathsf {aff}}\)-CIH, which is known to exist under the DDH assumption [1]. Let \(\mathsf {GGen}\) be a group generator that given \(1^{\lambda }\), generates a description of group of an \(\ell _p\)-bit prime order, and \(\mathsf {CIH}_\mathsf {aff}=(\mathsf {PrmGen}_\mathsf {aff},\mathsf {Eval}_\mathsf {aff})\) be a \(\varPhi ^{\mathsf {aff}}\)-CIH. For simplicity, we denote \(\mathsf {Eval}_\mathsf {CIH}(\mathsf {pp}_\mathsf {CIH}, \cdot )\) by \(\mathsf {CIH}_\mathsf {aff}(\cdot )\) when \(\mathsf {pp}_\mathsf {CIH}\) is clear. Our scheme \(\mathsf {CPRF}_{\mathsf {priv},\mathsf {std}}=(\mathsf {Setup},\mathsf {KeyGen},\mathsf {Eval},\mathsf {Constrain},\mathsf {CEval})\) is described as follows. Let \(n(\lambda )\) (often denoted as n for short) be an integer, which is used as the input length of \(\mathsf {CPRF}_{\mathsf {priv},\mathsf {std}}\).
- \(\mathsf {Setup}(1^{\lambda })\) :
-
: It generates \(\mathcal {G}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {GGen}(1^\lambda )\) to obtain the group description \(\mathcal {G}:= (\mathbb {G}, p)\), and runs \(\mathsf {pp}_\mathsf {CIH}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {PrmGen}_{\mathsf {aff}}(\mathcal {G}) \) to obtain
 . Recall that \(\mathsf {pp}_\mathsf {CIH}\) specifies the domain \(\mathbb {Z}_p^m\) and the range \(\mathcal {R}\) of \(\mathsf {CIH}_\mathsf {aff}\). It outputs
. Recall that \(\mathsf {pp}_\mathsf {CIH}\) specifies the domain \(\mathbb {Z}_p^m\) and the range \(\mathcal {R}\) of \(\mathsf {CIH}_\mathsf {aff}\). It outputs  .
. - \(\mathsf {KeyGen}(\mathsf {pp})\) :
-
: It chooses \(s_{i,b,j}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_p\) for \(i\in [n]\), \(b\in \{0,1\}\) and \(j\in [m]\), and outputs
 .
. - \(\mathsf {Eval}(\mathsf {msk},x)\) :
-
: It parses \(\{s_{i,b,j}\}_{i\in [n],b\in \{0,1\},j\in [m]}\leftarrow \mathsf {msk}\). It computes
 for \(j\in [m]\). Then it computes
for \(j\in [m]\). Then it computes  and outputs it.
and outputs it. - \(\mathsf {Constrain}(\mathsf {msk},c\in \{0,1,*\}^n)\)::
-
It parses \(\{s_{i,b}\}_{i\in [n],b\in \{0,1\}}\leftarrow \mathsf {msk}\), picks \(\alpha _j\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_p\) for \(j\in [m]\). Then it defines \(\{t_{i,b,j}\}_{i\in [n],b\in \{0,1\},j\in [m]}\) as follows. For all \(i\in [n]\), \(b\in \{0,1\}\) and \(j\in [m]\), it sets
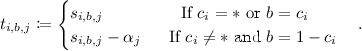
Then it outputs
 .
. - \(\mathsf {CEval}(\mathsf {sk}_c,x)\)::
-
It parses \(\{t_{i,b,j}\}_{i\in [n],b\in \{0,1\},j\in [m]}\leftarrow \mathsf {sk}_c\), computes

 for \(j\in [m]\) and
for \(j\in [m]\) and  , and outputs y.
, and outputs y.
Theorem 5
If \(\mathsf {CIH}\) is a \(\varPhi ^{\mathsf {aff}}\)-CIH and \(2^{2n-m \ell _p}\) is negligible, then the above scheme is a selectively single-key secure CPRF for  with selective single-key privacy.
with selective single-key privacy.
We prove the correctness and Theorem 5 in the full version [3].
Notes
- 1.
We note that the role of the constraining function f is “reversed” from the definition by Boneh and Waters [16], in the sense that the evaluation by a constrained key \(\mathsf {sk}_f\) is possible for inputs x with \(f(x) = 1\) in their definition, while it is possible for inputs x for \(f(x) = 0\) in our paper. Our treatment is the same as Brakerski and Vaikuntanathan [15].
- 2.
A constrained key in which a set of points is hard-wired enables us to compute an output if an input is not in the specified set.
- 3.
There are left and right constrained keys in which \(v_\ell \) and \(v_r\) are hard-wired, respectively. We can compute outputs by using the left (resp. right) constrained key if the first (resp. last) half of an input is equal to \(v_\ell \) (resp. \(v_r\)).
- 4.
This is the negation of bit-fixing functions, that is, \(f_c(x)=0\) if there exists an index i such that \(x_i \ne c_i\) (i-th bit of a constraint) and \(c_i \ne *\). It can be seen as a generalization of punctured predicates.
- 5.
For example, cyclic group \(\mathbb {H}\subset \mathbb {Z}^{*}_q\) of a prime order p such that \(q=2p+1\) where q is also a prime.
- 6.
In their sub-string match CPRFs, adversaries are not given access to the evaluation oracle, which gives outputs of a CPRF for queried inputs. We call such security no-evaluation security in this paper.
- 7.
Adversaries commit a function to be embedded in a constrained key at the beginning of the security experiment and have access to the evaluation oracle, which gives outputs of CPRFs for queried inputs.
- 8.
The L-DDHI assumption in a group \(\mathbb {H}\) of order p [4, 21] says that it is hard to distinguish \((g,g^{\alpha },g^{\alpha ^2},\ldots , g^{\alpha ^L},g^{1/\alpha })\) from \((g,g^{\alpha },g^{\alpha ^2},\ldots , g^{\alpha ^L},g^{z})\) where \(g\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {H},\alpha ,z \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_p\). See the full version [3] for the rigorous definition.
- 9.
The DDH assumption in a group \(\mathbb {G}\) of order q says that it is hard to distinguish \((g,g^x,g^y,g^{xy})\) from \((g,g^x,g^y,g^z)\) where \(g\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {G}, x,y,z\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_q\).
- 10.
Adversaries can decide a function for which it makes the key query at any time.
- 11.
Here, we identify a circuit that computes a function f with f itself.
- 12.
We can construct a universal circuit U whose depth is only constant times deeper than that of f by the result of Cook and Hoover [20]. It is well known that an \({\mathbf {NC}}^1\) circuit can be represented by a polynomial with polynomial degree (for example, this fact is used for functional encryption for \({\mathbf {NC}}^1\) [31]).
- 13.
Several works defined similar notions in different names such as related-key security. We use the name “correlated-input security” since we think it is the most suitable name for our usage.
- 14.
In the formal security definition, the function is parameterized by a public parameter generated by some setup procedure. We ignore the public parameter in the explanation below for simplicity. See Sect. 2.2 for the rigorous security definition for CIHs.
- 15.
- 16.
In this paper, a “class of functions” is a set of “sets of functions”. Each \(\mathcal {F}_{\lambda ,k}\) in \(\mathcal {F}\) considered for a CPRF is a set of functions parameterized by a security parameter \(\lambda \) and an input-length k.
- 17.
For a class of functions \(\mathcal {F}\) considered for CIHs, we allow each member of \(\mathcal {F}\) to be parameterized by not only \(\lambda \in \mathbb {N}\) but also \(z \in \{0,1\}^*\). The role of z is to associate the functions with a public parameter \(\mathsf {pp}\) generated by \(\mathsf {Setup}(1^{\lambda })\). See the security experiment in Fig. 2.
- 18.
If we fix an input of a PRF and view its key as a seed of a PRG, then the former can be seen as a latter.
- 19.
Here, we intentionally use the symbol \(\mathbb {H}\) and \(\mathsf {HGen}\) instead of \(\mathbb {G}\) and \(\mathsf {GGen}\). Looking ahead, in Sect. 4.2, the latter symbols will be used to represent yet another group of order q and corresponding group generator. There, we should require \(\mathbb {H}\) to be \(\mathbb {QR}_q\).
- 20.
According to the definition given in [3], we should give
 for all \(\lambda \in \mathbb {N}\) and \(n\in \mathbb {N}\). However, since
for all \(\lambda \in \mathbb {N}\) and \(n\in \mathbb {N}\). However, since  is the same for all \(\lambda \) if n is fixed in the case of the bit-fixing, we use this simpler notation.
is the same for all \(\lambda \) if n is fixed in the case of the bit-fixing, we use this simpler notation.
References
Abdalla, M., Benhamouda, F., Passelègue, A., Paterson, K.G.: Related-key security for pseudorandom functions beyond the linear barrier. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 77–94. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_5
Abusalah, H., Fuchsbauer, G., Pietrzak, K.: Constrained PRFs for unbounded inputs. In: Sako, K. (ed.) CT-RSA 2016. LNCS, vol. 9610, pp. 413–428. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-29485-8_24
Attrapadung, N., Matsuda, T., Nishimaki, R., Yamada, S., Yamakawa, T.: Constrained PRFs for \( {NC}^1\) in traditional groups. IACR Cryptol. ePrint Arch. 2018, 154 (2018)
Boneh, D., Boyen, X.: Short signatures without random oracles. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 56–73. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_4
Bellare, M., Cash, D.: Pseudorandom functions and permutations provably secure against related-key attacks. IACR Cryptol. ePrint Arch., 397 (2010). Version 20150729:233210. Preliminary Version Appeared in CRYPTO 2010
Bellare, M., Cash, D.: Pseudorandom functions and permutations provably secure against related-key attacks. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 666–684. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_36
Boneh, D., Franklin, M.K.: Identity-based encryption from the weil pairing. SIAM J. Comput. 32(3), 586–615 (2003)
Banerjee, A., Fuchsbauer, G., Peikert, C., Pietrzak, K., Stevens, S.: Key-homomorphic constrained pseudorandom functions. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 31–60. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_2
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S.P., Yang, K.: On the (im)possibility of obfuscating programs. J. ACM 59(2), 601–648 (2012)
Boyle, E., Goldwasser, S., Ivan, I.: Functional signatures and pseudorandom functions. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 501–519. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54631-0_29
Bitansky, N.: Verifiable random functions from non-interactive witness-indistinguishable proofs. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10678, pp. 567–594. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_19
Boneh, D., Kim, S., Montgomery, H.: Private puncturable PRFs from standard lattice assumptions. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part I. LNCS, vol. 10210, pp. 415–445. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_15
Boneh, D., Lewi, K., Wu, D.J.: Constraining pseudorandom functions privately. In: Fehr, S. (ed.) PKC 2017, Part II. LNCS, vol. 10175, pp. 494–524. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54388-7_17
Brakerski, Z., Tsabary, R., Vaikuntanathan, V., Wee, H.: Private constrained PRFs (and mode) from LWE. In: TCC 2017 (2017)
Brakerski, Z., Vaikuntanathan, V.: Constrained key-homomorphic PRFs from standard lattice assumptions. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 1–30. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_1
Boneh, D., Waters, B.: Constrained pseudorandom functions and their applications. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part II. LNCS, vol. 8270, pp. 280–300. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_15
Boyle, E., Gilboa, N., Ishai, Y.: Breaking the circuit size barrier for secure computation under DDH. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part I. LNCS, vol. 9814, pp. 509–539. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_19
Canetti, R., Chen, Y.: Constraint-hiding constrained PRFs for NC1 from LWE. In: EUROCRYPT 2017, Part I, pp. 446–476 (2017)
Cohen, A., Goldwasser, S., Vaikuntanathan, V.: Aggregate pseudorandom functions and connections to learning. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 61–89. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_3
Cook, S.A., Hoover, H.J.: A depth-universal circuit. SIAM J. Comput. 14(4), 833–839 (1985)
Camenisch, J., Hohenberger, S., Lysyanskaya, A.: Compact E-Cash. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 302–321. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_18
Döttling, N., Garg, S.: Identity-based encryption from the diffie-hellman assumption. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 537–569. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_18
Deshpande, A., Koppula, V., Waters, B.: Constrained pseudorandom functions for unconstrained inputs. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 124–153. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_5
Fuchsbauer, G., Konstantinov, M., Pietrzak, K., Rao, V.: Adaptive security of constrained PRFs. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part II. LNCS, vol. 8874, pp. 82–101. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45608-8_5
Garg, S., Gentry, C., Halevi, S.: Candidate multilinear maps from ideal lattices. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 1–17. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_1
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. SIAM J. Comput. 45(3), 882–929 (2016)
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM 33(4), 792–807 (1986)
Goyal, R., Hohenberger, S., Koppula, V., Waters, B.: A generic approach to constructing and proving verifiable random functions. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10678, pp. 537–566. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_18
Goldenberg, D., Liskov, M.: On related-secret pseudorandomness. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 255–272. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_16
Goyal, V., O’Neill, A., Rao, V.: Correlated-input secure hash functions. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 182–200. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_12
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_11
Hofheinz, D., Kamath, A., Koppula, V., Waters, B.: Adaptively secure constrained pseudorandom functions. IACR Cryptol. ePrint Arch. 2014, 720 (2014)
Hohenberger, S., Koppula, V., Waters, B.: Adaptively secure puncturable pseudorandom functions in the standard model. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015, Part I. LNCS, vol. 9452, pp. 79–102. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_4
Ishai, Y., Kilian, J., Nissim, K., Petrank, E.: Extending oblivious transfers efficiently. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 145–161. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_9
Kiayias, A., Papadopoulos, S., Triandopoulos, N., Zacharias, T.: Delegatable pseudorandom functions and applications. ACMCCS 2013, 669–684 (2013)
Naor, M., Reingold, O.: Number-theoretic constructions of efficient pseudo-random functions. J. ACM 51(2), 231–262 (2004)
Peikert, C., Shiehian, S.: Privately constraining and programming PRFs, the LWE way. In: Abdalla, M., Dahab, R. (eds.) PKC 2018. LNCS, vol. 10770, pp. 675–701. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76581-5_23
Yamada, S.: Asymptotically compact adaptively secure lattice IBEs and verifiable random functions via generalized partitioning techniques. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part III. LNCS, vol. 10403, pp. 161–193. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_6
Zhandry, M.: How to avoid obfuscation using witness PRFs. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016, Part II. LNCS, vol. 9563, pp. 421–448. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49099-0_16
Acknowledgement
We thank Keita Xagawa for letting us know the relation between CIH and RKA-PRG. The first, second, and fourth authors were supported by JST CREST Grant No. JPMJCR1688. The fourth author was supported by JSPS KAKENHI Grant Number 16K16068.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Attrapadung, N., Matsuda, T., Nishimaki, R., Yamada, S., Yamakawa, T. (2018). Constrained PRFs for \(\mathrm{NC}^1\) in Traditional Groups. In: Shacham, H., Boldyreva, A. (eds) Advances in Cryptology – CRYPTO 2018. CRYPTO 2018. Lecture Notes in Computer Science(), vol 10992. Springer, Cham. https://doi.org/10.1007/978-3-319-96881-0_19
Download citation
DOI: https://doi.org/10.1007/978-3-319-96881-0_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96880-3
Online ISBN: 978-3-319-96881-0
eBook Packages: Computer ScienceComputer Science (R0)





 . We call a CPRF for this function class simply a CPRF for circuits. If a CPRF supports functions computable by polynomial-sized boolean circuits with depth
. We call a CPRF for this function class simply a CPRF for circuits. If a CPRF supports functions computable by polynomial-sized boolean circuits with depth  ::
::
 ::
::
 .
.
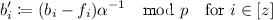
 and outputs X. Otherwise it outputs
and outputs X. Otherwise it outputs  and outputs
and outputs  against the no-evaluation adversary
against the no-evaluation adversary  . It outputs
. It outputs  .
. .
.
 .
. for
for  (
( for
for  .
.
 .
.
 .
. .
. . It then runs
. It then runs  .
. for
for  . It then sets
. It then sets  and runs
and runs  to obtain
to obtain  (
( ) for
) for  . Recall that
. Recall that  .
. .
. for
for  and outputs it.
and outputs it.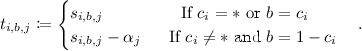
 .
.
 for
for  , and outputs y.
, and outputs y. for all
for all  is the same for all
is the same for all 