Abstract
We aim to understand the best possible security of a (bidirectional) cryptographic channel against an adversary that may arbitrarily and repeatedly learn the secret state of either communicating party. We give a formal security definition and a proven-secure construction. This construction provides better security against state compromise than the Signal Double Ratchet Algorithm or any other known channel construction. To facilitate this we define and construct new forms of public-key encryption and digital signatures that update their keys over time.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Cryptographic Channel
- Ciphertext
- Verification Key
- Hierarchical Identity-based Encryption (HIBE)
- Decoding Accuracy
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
End-to-end encrypted communication is becoming a usable reality for the masses in the form of secure messaging apps. However, chat sessions can be extremely long-lived and their secrets are stored on end user devices, so they are particularly vulnerable to having their cryptographic secrets exfiltrated to an attacker by malware or physical access to the device. The Signal protocol [33] by Open Whisper Systems tries to mitigate this threat by continually updating the key used for encryption. Beyond its use in the Signal messaging app, this protocol has been adopted by a number of other secure messaging apps. This includes being used by default in WhatsApp and as part of secure messaging modes of Facebook Messenger, Google Allo, and Skype.
WhatsApp alone has 1 billion daily active users [43]. It is commonly agreed in the cryptography and security community that the Signal protocol is secure. However, the protocol was designed without an explicitly defined security notion. This raises the questions: what security does it achieve and could we do better?
In this work we study the latter question, aiming to understand the best possible security of two-party communication in the face of state exfiltration. We formally define this notion of security and design a scheme that provably achieves it.
\({\underline{\textsf {Security\, against\, compromise.}}}\) When a party’s secret state is exposed we would like both that the security of past messages and (as soon as possible) the security of future messages not be damaged. These notions have been considered in a variety of contexts with differing terminology. The systemization of knowledge paper on secure messaging [42] by Unger et al. evaluates and systematizes a number of secure messaging systems. In it they describe a variety of terms for these types of security including “forward secrecy,” “backwards secrecy,” “self-healing,” and “future secrecy” and note that they are “controversial and vague.” Cohn-Gordon et al. [15] study the future direction under the term of post-compromise security and similarly discuss the terms “future secrecy,” “healing,” and “bootstrapping” and note that they are “intuitive” but “not well-defined.” Our security notion intuitively captures any of these informal terms, but we avoid using any of them directly by aiming generically for the best possible security against compromise.
\({\underline{\textsf {Channels.}}}\) The standard model for studying secure two party communication is that of the (cryptographic) channel. The first attempts to consider the secure channel as a cryptographic object were made by Shoup [39] and Canetti [11]. It was then formalized by Canetti and Krawczyk [13] as a modular way to combine a key exchange protocol with authenticated encryption, which covers both privacy and integrity. Krawczyk [28] and Namprempre [32] study what are the necessary and sufficient security notions to build a secure channel from these primitives.
Modern definitions of channels often draw from the game-based notion of security for stateful authenticated-encryption as defined by Bellare et al. [4]. We follow this convention which assumes initial generation of keys is trusted. In addition to requiring that a channel provides integrity and privacy of the encrypted data, we will require integrity for associated data as introduced by Rogaway [36].
Recently Marson and Poettering [30] closed a gap in the modeling of two-party communication by capturing the bidirectional nature of practical channels in their definitions. We work with their notion of bidirectional channels because it closely models the behavior desired in practice and the bidirectional nature of communication allows us to achieve a fine-grained security against compromise.
\({\underline{\textsf {Definitional\, contributions.}}}\) This paper aims to specify and achieve the best possible security of a bidirectional channel against state compromise. We provide a formal, game-based definition of security and a construction that provably achieves it. We analyze our construction in a concrete security framework [2] and give precise bounds on the advantage of an attacker.
To derive the best possible notion of security against state compromise we first specify a basic input-output interface via a game that describes how the adversary interacts with the channel. This corresponds roughly to combining the integrity and confidentiality games of [30] and adding an oracle that returns the secret state of a specified user to the adversary. Then we specify several attacks that break the security of any channel. We define our final security notion by minimally extending the initial interface game to disallow these unavoidable attacks while allowing all other behaviors. Our security definition is consequently the best possible with respect to the specified interface because our attacks rule out the possibility of any stronger notion.
One security notion is an all-in-one notion in the style of [37] that simultaneously requires integrity and privacy of the channel. It asks for the maximal possible security in the face of the exposure of either party’s state. A surprising requirement of our definition is that given the state of a user the adversary should not be able to decrypt ciphertexts sent by that user or send forged ciphertexts to that user.
\({\underline{\textsf {Protocols\, that\, update\, their\, keys.}}}\) The OTR (Off-the-Record) messaging protocol [10] is an important predecessor to Signal. It has parties repeatedly exchange Diffie-Hellman elements to derive new keys. The Double Ratchet Algorithm of Signal uses a similar Diffie-Hellman update mechanism and extends it by using a symmetric key-derivation function to update keys when there is no Diffie-Hellman update available. Both methods of updating keys are often referred to as ratcheting (a term introduced by Langley [29]). While the Double Ratchet Algorithm was explicitly designed to achieve strong notions of security against state compromise with respect to privacy, the designers explicitly consider security against a passive eavesdropper [21]; authenticity in the face of compromise is out of scope.
The first academic security analysis of Signal was due to Cohn-Gordan et al. [14]. They only considered the security of the key exchange underlying the Double Ratchet Algorithm and used a security definition explicitly tailored to understanding its security instead of being widely applicable to any scheme.
Work by Bellare et al. [7] sought to formally understand ratcheting as an independent primitive, introducing the notions of (one-directional) ratcheted key exchange and ratcheted encryption. In their model a compromise of the receiving party’s secrets permanently and irrevocably disrupts all security, past and future. Further they strictly separate the exchange of key update information from the exchange of messages. Such a model cannot capture a protocol like the Double Ratchet Algorithm for which the two are inextricably combined. On the positive side, they did explicitly model authenticity in the face of compromise.
In [26], Günther and Mazaheri study a key update mechanism introduced in TLS 1.3. Their security definition treats update messages as being out-of-band and thus implicitly authenticated. Their definition is clearly tailored to understand TLS 1.3 specifically.
Instead of analyzing an existing scheme, we strive to understand the best possible security with respect to both privacy and authenticity in the face of state compromise. The techniques we use to achieve this differ from those underlying the schemes discussed above, because all of them rely on exchanging information to create a shared symmetric key that is ultimately used for encryption. Our security notion is not achievable by a scheme of this form and instead requires that asymmetric primitives be used throughout.
Consequently, our scheme is more computationally intensive than those mentioned above. However, as a part of OTR or the Double Ratchet Algorithm, when users are actively sending messages back and forth (the case where efficiency is most relevant), they will be performing asymmetric Diffie-Hellman based key updates prior to most message encryptions. This indicates that the overhead of extra computation with asymmetric techniques is not debilitating in our motivating context of secure messaging. However, the asymmetric techniques we require are likely less efficient than Diffie-Hellman computations so we do not currently know whether our scheme meets realistic efficiency requirements.
\({\underline{\textsf {Our\, construction.}}}\) Our construction of a secure channel is given in Sect. 6.1. It shows how to generically build the channel from a collision-resistant hash function, a public-key encryption scheme, and a digital signature scheme. The latter two require new versions of the primitives that we describe momentarily.
The hash function is used to store transcripts of the communication in the form of hashes of all sent or received ciphertexts. These transcripts are included as part of every ciphertext and a user will not accept a ciphertext with transcripts that do not match those it has stored locally. Every ciphertext sent by a user is signed by their current digital signature signing key and includes the verification key corresponding to their next signing key. Similarly a user will include a new encryption key with every ciphertext they send. The sending user will use the most recent encryption key they have received from the other user and the receiving user will delete all decryption keys that are older than the one most recently used by the sender.
\({\underline{\textsf {New\, notions \,of \,public-key\, encryption \,and\, digital\, signatures.}}}\) Our construction uses new forms of public-key encryption and digital signatures that update their keys over time, which we define in Sect. 3. The former updates its keys with every ciphertext. We refer to it as key-updating public-key encryption. The latter includes extra algorithms that allow the keys to be updated with respect to an arbitrary string. We refer to it as key-updatable digital signature schemes. In our construction a user updates their signing key with their transcript every time they receive a ciphertext.
For public-key encryption we consider encryption with labels and require an IND-CCA style security be maintained even if the adversary is given the decryption key after all challenge ciphertexts have been decrypted or an adversarially generated ciphertext has been decrypted. We show how to construct such scheme from hierarchical identity-based encryption [23].
For digital signatures, security requires that an adversary is unable to forge a signature even given the signing key as long as the sequence of strings used to update it is not a prefix of the sequence of strings used to update the verification key. We additionally require that the scheme has unique signatures (i.e. for any sequence of updates and any message an adversary can only find one signature that will verify). We show how to construct this from a digital signature scheme that is forward secure [5] and has unique signatures.
\({\underline{\textsf {Related\, work.}}}\) Several works [9, 22] extended the definitions of channels to address the stream-based interface provided by channels like TLS, SSH, and QUIC. Our primary motivation is to build a channel for messaging where an atomic interface for messages is more appropriate.
Numerous areas of research within cryptography are motivated by the threat of key compromise. These include key-insulated cryptography [18,19,20], secret sharing [31, 38, 41], threshold cryptography [16], proactive cryptography [34], and forward security [17, 25]. Forward security, in particular, was introduced in the context of key-exchange [17, 25] but has since been considered for a variety of primitives including symmetric [8] and asymmetric encryption [12] and digital signature schemes [5]. Green and Miers [24] propose using puncturable encryption for forward secure asynchronous messaging.
In concurrent and independent work, Poettering and Rösler [35] extend the definitions of ratcheted key exchange from [7] to be bidirectional. Their security definition is conceptually similar to our definition for bidirectional channels because both works aim to achieve strong notions of security against an adversary that can arbitrarily and repeatedly learn the secret state of either communicating party. In constructing a secure ratcheted key exchange scheme they make use of a key-updatable key encapsulation mechanism (KEM), a new primitive they introduce in their work. The key-updatable nature of this is conceptually similar to that of the key-updatable digital signature schemes we introduce in our work. To construct such a KEM they make use of hierarchical identity-based encryption in a manner similar to how we construct key-updating public-key encryption. The goal of their work differs from ours; they only consider security for the exchange of symmetric keys while we do so for the exchange of messages.
2 Preliminaries
\({\underline{\textsf {Notation\, and\, conventions.}}}\) Let \({{\mathbb N}} =\{0, 1, 2, \ldots \}\) be the set of non-negative integers. Let \(\varepsilon \) denote the empty string. If \(x\in \{0,1\}^*\) is a string then |x| denotes its length. By \(x{\,\Vert \,}y\) we denote the concatenation of strings x and y. If \({X}\) is a finite set, we let  denote picking an element of \({X}\) uniformly at random and assigning it to x. By \(({X})^n\) we denote the n-ary Cartesian product of \({X}\). We let \(x_1\leftarrow x_2\leftarrow \dots \leftarrow x_n \leftarrow v\) denote assigning the value v to each variable \(x_i\) for \(i=1,\dots ,n\).
denote picking an element of \({X}\) uniformly at random and assigning it to x. By \(({X})^n\) we denote the n-ary Cartesian product of \({X}\). We let \(x_1\leftarrow x_2\leftarrow \dots \leftarrow x_n \leftarrow v\) denote assigning the value v to each variable \(x_i\) for \(i=1,\dots ,n\).
If \(\mathbf {mem}\) is a table, we use \(\mathbf {mem}[p]\) to denote the element of the table that is indexed by p. By \(\mathbf {mem}[0,\dots ,\infty ]\leftarrow v\) we denote initializing all elements of \(\mathbf {mem}\) to v. For \(a,b\in {{\mathbb N}} \) we let \(v\leftarrow \mathbf {mem}[a,\dots ,b]\) denote setting v equal to the tuple obtained by removing all \(\bot \) elements from \((\mathbf {mem}[a],\mathbf {mem}[a+1],\dots ,\mathbf {mem}[b])\). It is the empty vector () if all of these table entries are \(\bot \) or if \(a>b\). A tuple \({\varvec{x}}=(x_1,\dots )\) specifies a uniquely decodable concatenation of strings \(x_1,\dots \). We say \({\varvec{x}}\sqsubseteq {\varvec{y}}\) if \({\varvec{x}}\) is a prefix of \({\varvec{y}}\). More formally, \((x_1,\dots ,x_n)\sqsubseteq (y_1,\dots ,y_m)\) if \(n\le m\) and \(x_i=y_i\) for all \(i\in \{1,\dots ,n\}\).
Algorithms may be randomized unless otherwise indicated. Running time is worst case. If A is an algorithm, we let \(y \leftarrow A(x_1,\ldots ;r)\) denote running A with random coins r on inputs \(x_1,\ldots \) and assigning the output to y. Any state maintained by an algorithm will explicitly be shown as input and output of that algorithm. We let  denote picking r at random and letting \(y \leftarrow A(x_1,\ldots ;r)\). We omit the semicolon when there are no inputs other than the random coins. We let \([A(x_1,\ldots )]\) denote the set of all possible outputs of A when invoked with inputs \(x_1,\ldots \). Adversaries are algorithms. The instruction \({\mathbf {abort}}(x_1,\dots )\) is used by an adversary to immediately halt with output \((x_1,\dots )\).
denote picking r at random and letting \(y \leftarrow A(x_1,\ldots ;r)\). We omit the semicolon when there are no inputs other than the random coins. We let \([A(x_1,\ldots )]\) denote the set of all possible outputs of A when invoked with inputs \(x_1,\ldots \). Adversaries are algorithms. The instruction \({\mathbf {abort}}(x_1,\dots )\) is used by an adversary to immediately halt with output \((x_1,\dots )\).
We use a special symbol \(\bot \not \in \{0,1\}^*\) to denote an empty table position, and we also return it as an error code indicating an invalid input. An algorithm may not accept \(\bot \) as input. If \(x_i=\bot \) for some i when executing \((y_1,\dots )\leftarrow A(x_1\dots )\) we assume that \(y_j=\bot \) for all j. We assume that adversaries never pass \(\bot \) as input to their oracles.
We use the code based game playing framework of [6]. (See Fig. 1 for an example of a game.) We let \(\Pr [\mathrm {G}]\) denote the probability that game \(\mathrm {G}\) returns \(\mathsf {true}\). In code, tables are initially empty. We adopt the convention that the running time of an adversary means the worst case execution time of the adversary in the game that executes it, so that time for game setup steps and time to compute answers to oracle queries is included.
\({\underline{\textsf {Function\, families.}}}\) A family of functions \(\mathsf {H}\) specifies algorithms \(\mathsf {\mathsf {H}.Kg}\) and \(\mathsf {\mathsf {H}.Ev}\), where \(\mathsf {\mathsf {H}.Ev}\) is deterministic. Key generation algorithm \(\mathsf {\mathsf {H}.Kg}\) returns a key  . Evaluation algorithm \(\mathsf {\mathsf {H}.Ev}\) takes
. Evaluation algorithm \(\mathsf {\mathsf {H}.Ev}\) takes  and an input \(x\in \{0,1\}^*\) to return an output y, denoted by
and an input \(x\in \{0,1\}^*\) to return an output y, denoted by  .
.
\({\underline{\textsf {Collision-resistant\, functions.}}}\) Consider game \(\mathrm {CR}\) of Fig. 1 associated to a function family \(\mathsf {H}\) and an adversary \(\mathcal {A}_{\mathsf {H}}\). The game samples a random key  for function family \(\mathsf {H}\). In order to win the game, adversary \(\mathcal {A}_{\mathsf {H}}\) has to find two distinct messages \(m_0, m_1\) such that
for function family \(\mathsf {H}\). In order to win the game, adversary \(\mathcal {A}_{\mathsf {H}}\) has to find two distinct messages \(m_0, m_1\) such that  . The advantage of \(\mathcal {A}_{\mathsf {H}}\) in breaking the \(\mathrm {CR}\) security of \(\mathsf {H}\) is defined as \(\mathsf {Adv}^{\mathsf {cr}}_{\mathsf {H}}(\mathcal {A}_{\mathsf {H}}) = \Pr [\mathrm {CR}_{\mathsf {H}}^{\mathcal {A}_{\mathsf {H}}}]\).
. The advantage of \(\mathcal {A}_{\mathsf {H}}\) in breaking the \(\mathrm {CR}\) security of \(\mathsf {H}\) is defined as \(\mathsf {Adv}^{\mathsf {cr}}_{\mathsf {H}}(\mathcal {A}_{\mathsf {H}}) = \Pr [\mathrm {CR}_{\mathsf {H}}^{\mathcal {A}_{\mathsf {H}}}]\).
\({\underline{\textsf {Digital\, signature\, schemes.}}}\) A digital signature scheme \(\mathsf {DS}\) specifies algorithms \(\mathsf {\mathsf {DS}.Kg}\), \(\mathsf {\mathsf {DS}.Sign}\) and \(\mathsf {\mathsf {DS}.Vrfy}\), where \(\mathsf {\mathsf {DS}.Vrfy}\) is deterministic. Associated to \(\mathsf {DS}\) is a key generation randomness space \(\mathsf {\mathsf {DS}.KgRS}\) and signing algorithm’s randomness space \(\mathsf {\mathsf {DS}.SignRS}\). Key generation algorithm \(\mathsf {\mathsf {DS}.Kg}\) takes randomness \(z\in \mathsf {\mathsf {DS}.KgRS}\) to return a signing key  and a verification key
and a verification key  , denoted by
, denoted by  . Signing algorithm \(\mathsf {\mathsf {DS}.Sign}\) takes
. Signing algorithm \(\mathsf {\mathsf {DS}.Sign}\) takes  , a message \(m\in \{0,1\}^*\) and randomness \(z\in \mathsf {\mathsf {DS}.SignRS}\) to return a signature \(\sigma \), denoted by
, a message \(m\in \{0,1\}^*\) and randomness \(z\in \mathsf {\mathsf {DS}.SignRS}\) to return a signature \(\sigma \), denoted by  . Verification algorithm \(\mathsf {\mathsf {DS}.Vrfy}\) takes
. Verification algorithm \(\mathsf {\mathsf {DS}.Vrfy}\) takes  , \(\sigma \), and m to return a decision \(t\in \{\mathsf {true},\mathsf {false}\}\) regarding whether \(\sigma \) is a valid signature of m under
, \(\sigma \), and m to return a decision \(t\in \{\mathsf {true},\mathsf {false}\}\) regarding whether \(\sigma \) is a valid signature of m under  , denoted by
, denoted by  . The correctness condition for \(\mathsf {DS}\) requires that
. The correctness condition for \(\mathsf {DS}\) requires that  for all
for all  , all \(m\in \{0,1\}^*\), and all
, all \(m\in \{0,1\}^*\), and all  .
.
We define the min-entropy of algorithm \(\mathsf {\mathsf {DS}.Kg}\) as \(\mathrm {H}_{\infty }(\mathsf {\mathsf {DS}.Kg})\), such that

The probability is defined over the random coins used for \(\mathsf {\mathsf {DS}.Kg}\). Note that the min-entropy is defined with respect to verification keys, regardless of the corresponding values of the secret keys.
3 New Asymmetric Primitives
In this section we define key-updatable digital signatures and key-updating public-key encryption. The former allows its keys to be updated with arbitrary strings. The latter updates its keys with every ciphertext that is sent/received. While in general one would prefer the size of keys, signatures, and ciphertexts to be constant we will be willing to accept schemes for which these grow linearly in the number of updates. As we will discuss later, these are plausibly acceptable inefficiencies for our use cases.
We specify multi-user security definitions for both primitives, because it allows tighter reductions when we construct a channel from these primitives. Single-user variants of these definitions are obtained by only allowing the adversary to interact with one user and can be shown to imply the multi-user versions by a standard hybrid argument. Starting with [1] constructions have been given for a variety of primitives that allow multi-user security to be proven without the factor q security loss introduced by a hybrid argument. If analogous constructions can be found for our primitives then our results will give tight bounds on the security of our channel.
3.1 Key-Updatable Digital Signature Schemes
We start by formally defining the syntax and correctness of a key-updatable digital signature scheme. Then we specify a security definition for it. We will briefly sketch how to construct such a scheme, but leave the details to [27].
\({\underline{\textsf {Syntax\, and\, correctness.}}}\) A key-updatable digital signature scheme is a digital signature scheme with additional algorithms \(\mathsf {\mathsf {DS}.UpdSk}\) and \(\mathsf {\mathsf {DS}.UpdVk}\), where \(\mathsf {\mathsf {DS}.UpdVk}\) is deterministic. Signing-key update algorithm \(\mathsf {\mathsf {DS}.UpdSk}\) takes a signing key  and a key update information \(\varDelta \in \{0,1\}^*\) to return a new signing key
and a key update information \(\varDelta \in \{0,1\}^*\) to return a new signing key  , denoted by
, denoted by  . Verification-key update algorithm \(\mathsf {\mathsf {DS}.UpdVk}\) takes a verification key
. Verification-key update algorithm \(\mathsf {\mathsf {DS}.UpdVk}\) takes a verification key  and a key update information \(\varDelta \in \{0,1\}^*\) to return a new verification key
and a key update information \(\varDelta \in \{0,1\}^*\) to return a new verification key  , denoted by
, denoted by  .
.
For compactness, when \(\varvec{\varDelta }= (\varDelta _1, \varDelta _2, \ldots )\) we sometimes write  to denote updating the key via
to denote updating the key via  for \(i=1,\ldots ,n\) and then evaluating
for \(i=1,\ldots ,n\) and then evaluating  .
.
The key-update correctness condition requires that signatures must verify correctly as long as the signing and the verification keys are both updated with the same sequence of key update information \(\varvec{\varDelta }= (\varDelta _1, \varDelta _2, \ldots )\). To formalize this, consider game \(\mathrm {DSCORR}\) of Fig. 2, associated to a key-updatable digital signature scheme \(\mathsf {DS}\) and an adversary \(\mathcal {C}\). The advantage of an adversary \(\mathcal {C}\) against the correctness of \(\mathsf {DS}\) is given by \(\mathsf {Adv}^{\mathsf {dscorr}}_{\mathsf {DS}}(\mathcal {C})=\Pr [\mathrm {DSCORR}^{\mathcal {C}}_{\mathsf {DS}}]\). We require that \(\mathsf {Adv}^{\mathsf {dscorr}}_{\mathsf {DS}}(\mathcal {C}) = 0\) for all (even unbounded) adversaries \(\mathcal {C}\). See Sect. 4 for discussion on game-based definitions of correctness.
\({\underline{\textsf {Signature\, uniqueness.}}}\) We will be interested in schemes for which there is only a single signature that will be accepted for any message  and any sequence of updates \(\varvec{\varDelta }\). Consider game \(\mathrm {UNIQ}\) of Fig. 1, associated to a key-updatable digital signature scheme \(\mathsf {DS}\) and an adversary \(\mathcal {B}_{\mathsf {DS}}\). The adversary \(\mathcal {B}_{\mathsf {DS}}\) can call the oracle \(\textsc {NewUser}\) arbitrarily many times with a user identifier \(\varLambda \) and be given the randomness used to generate the keys of \(\varLambda \). The adversary ultimately outputs a user id \(\varLambda \), message
and any sequence of updates \(\varvec{\varDelta }\). Consider game \(\mathrm {UNIQ}\) of Fig. 1, associated to a key-updatable digital signature scheme \(\mathsf {DS}\) and an adversary \(\mathcal {B}_{\mathsf {DS}}\). The adversary \(\mathcal {B}_{\mathsf {DS}}\) can call the oracle \(\textsc {NewUser}\) arbitrarily many times with a user identifier \(\varLambda \) and be given the randomness used to generate the keys of \(\varLambda \). The adversary ultimately outputs a user id \(\varLambda \), message  , signatures \(\sigma _1,\sigma _2\), and key update vector \(\varvec{\varDelta }\). It wins if the signatures are distinct and both verify for
, signatures \(\sigma _1,\sigma _2\), and key update vector \(\varvec{\varDelta }\). It wins if the signatures are distinct and both verify for  when the verification key of \(\varLambda \) is updated with \(\varvec{\varDelta }\). The advantage of \(\mathcal {B}_{\mathsf {DS}}\) in breaking the \(\mathrm {UNIQ}\) security of \(\mathsf {DS}\) is defined by \(\mathsf {Adv}^{\mathsf {uniq}}_{\mathsf {DS}}(\mathcal {B}_{\mathsf {DS}})=\Pr [\mathrm {UNIQ}^{\mathcal {B}_{\mathsf {DS}}}_{\mathsf {DS}}]\).
when the verification key of \(\varLambda \) is updated with \(\varvec{\varDelta }\). The advantage of \(\mathcal {B}_{\mathsf {DS}}\) in breaking the \(\mathrm {UNIQ}\) security of \(\mathsf {DS}\) is defined by \(\mathsf {Adv}^{\mathsf {uniq}}_{\mathsf {DS}}(\mathcal {B}_{\mathsf {DS}})=\Pr [\mathrm {UNIQ}^{\mathcal {B}_{\mathsf {DS}}}_{\mathsf {DS}}]\).
\({\underline{\textsf {Signature\, unforgeability\, under\, exposures.}}}\) Our main security notion for signatures asks that the adversary not be able to create signatures for any key update vector \(\varvec{\varDelta }\) unless it was given a signature for that key update vector or given the signing key such that the vector of strings it had been updated with was a prefix of \(\varvec{\varDelta }\). Consider game \(\mathrm {UFEXP}\) of Fig. 3, associated to a key-updatable digital signature scheme \(\mathsf {DS}\) and an adversary \(\mathcal {A}_{\mathsf {DS}}\).
The adversary \(\mathcal {A}_{\mathsf {DS}}\) can call the oracle \(\textsc {NewUser}\) arbitrarily many times for any user identifier \(\varLambda \) and be given the verification key for that user. Then it can interact with user \(\varLambda \) via three different oracles. Via calls to \(\textsc {Upd}\) with a string \(\varDelta \) it requests that the signing key for the specified user be updated with \(\varDelta \). Via calls to \(\textsc {Sign}\) with message  it asks for a signature of
it asks for a signature of  using the signing key for the specified user. When it does so the signing key is erased so it can no longer interact with that user and \(\varvec{\varDelta }^*[\varLambda ]\) is used to store the vector of strings the key was updated with.Footnote 1 Via calls to \(\textsc {Exp}\) it can ask to be given the current signing key of the specified user. When it does so \(\varvec{\varDelta }'[\varLambda ]\) is used to store the vector of strings the key was updated with.
using the signing key for the specified user. When it does so the signing key is erased so it can no longer interact with that user and \(\varvec{\varDelta }^*[\varLambda ]\) is used to store the vector of strings the key was updated with.Footnote 1 Via calls to \(\textsc {Exp}\) it can ask to be given the current signing key of the specified user. When it does so \(\varvec{\varDelta }'[\varLambda ]\) is used to store the vector of strings the key was updated with.
At the end of the game the adversary outputs a user id \(\varLambda \), signature \(\sigma \), message  , and key update vector \(\varvec{\varDelta }\). The adversary has cheated if it previously received \(\sigma \) as the result of calling
, and key update vector \(\varvec{\varDelta }\). The adversary has cheated if it previously received \(\sigma \) as the result of calling  and \(\varvec{\varDelta }=\varvec{\varDelta }^*[\varLambda ]\), or if it exposed the signing key of \(\varLambda \) and \(\varvec{\varDelta }'[\varLambda ]\) is a prefix of \(\varvec{\varDelta }\). It wins if it has not cheated and the signature it output verifies for
and \(\varvec{\varDelta }=\varvec{\varDelta }^*[\varLambda ]\), or if it exposed the signing key of \(\varLambda \) and \(\varvec{\varDelta }'[\varLambda ]\) is a prefix of \(\varvec{\varDelta }\). It wins if it has not cheated and the signature it output verifies for  when the verification key of \(\varLambda \) is updated with \(\varvec{\varDelta }\). The advantage of \(\mathcal {A}_{\mathsf {DS}}\) in breaking the \(\mathrm {UFEXP}\) security of \(\mathsf {DS}\) is defined by \(\mathsf {Adv}^{\mathsf {ufexp}}_{\mathsf {DS}}(\mathcal {A}_{\mathsf {DS}}) = \Pr [\mathrm {UFEXP}^{\mathcal {A}_{\mathsf {DS}}}_{\mathsf {DS}}]\).
when the verification key of \(\varLambda \) is updated with \(\varvec{\varDelta }\). The advantage of \(\mathcal {A}_{\mathsf {DS}}\) in breaking the \(\mathrm {UFEXP}\) security of \(\mathsf {DS}\) is defined by \(\mathsf {Adv}^{\mathsf {ufexp}}_{\mathsf {DS}}(\mathcal {A}_{\mathsf {DS}}) = \Pr [\mathrm {UFEXP}^{\mathcal {A}_{\mathsf {DS}}}_{\mathsf {DS}}]\).
\({\underline{\textsf {Construction.}}}\) In [27] we use a forward secure [5] key-evolving signature scheme with unique signatures to construct a signature scheme secure with respect to both of the above definitions. Roughly, a key-evolving signature scheme is like a key-updatable digital signature scheme that can only update with \(\varDelta =\varepsilon \). In order to enable updates with respect to arbitrary key update information, we sign each update string with the current key prior to evolving the key, and then include these intermediate signatures with our final signature.
3.2 Key-Updating Public-Key Encryption Schemes
We start by formally defining the syntax and correctness of a key-updating public-key encryption. Then we specify a security definition for it. We will briefly sketch how to construct such a scheme, but leave the details to [27]. We consider public-key encryption with labels as introduced by Shoup [40].
\({\underline{\textsf {Syntax\, and\, correctness.}}}\) A key-updating public-key encryption scheme \(\mathsf {PKE}\) specifies algorithms \(\mathsf {\mathsf {PKE}.Kg}\), \(\mathsf {\mathsf {PKE}.Enc}\), \(\mathsf {\mathsf {PKE}.Dec}\). Associated to \(\mathsf {PKE}\) is a key generation randomness space \(\mathsf {\mathsf {PKE}.KgRS}\) and encryption randomness space \(\mathsf {\mathsf {PKE}.EncRS}\). Key generation algorithm \(\mathsf {\mathsf {PKE}.Kg}\) takes randomness \(z\in \mathsf {\mathsf {PKE}.KgRS}\) to return an encryption key  and a decryption key
and a decryption key  , denoted by
, denoted by  . Encryption algorithm \(\mathsf {\mathsf {PKE}.Enc}\) takes
. Encryption algorithm \(\mathsf {\mathsf {PKE}.Enc}\) takes  , a label \(\ell \in \{0,1\}^*\), a message
, a label \(\ell \in \{0,1\}^*\), a message  and randomness \(z\in \mathsf {\mathsf {PKE}.EncRS}\) to return a new encryption key
and randomness \(z\in \mathsf {\mathsf {PKE}.EncRS}\) to return a new encryption key  and a ciphertext
and a ciphertext  , denoted by
, denoted by  . Decryption algorithm \(\mathsf {\mathsf {PKE}.Dec}\) takes
. Decryption algorithm \(\mathsf {\mathsf {PKE}.Dec}\) takes  to return a new decryption key
to return a new decryption key  and a message \(m\in \{0,1\}^*\), denoted by
and a message \(m\in \{0,1\}^*\), denoted by  .
.
The correctness condition requires that ciphertexts decrypt correctly as long as they are received in the same order they were created and with the same labels. To formalize this, consider game \(\mathrm {PKECORR}\) of Fig. 2, associated to a key-updating public-key encryption scheme \(\mathsf {PKE}\) and an adversary \(\mathcal {C}\). The advantage of an adversary \(\mathcal {C}\) against the correctness of \(\mathsf {PKE}\) is given by \(\mathsf {Adv}^{\mathsf {pkecorr}}_{\mathsf {PKE}}(\mathcal {C})=\Pr [\mathrm {PKECORR}^{\mathcal {C}}_{\mathsf {PKE}}]\). Correctness requires that \(\mathsf {Adv}^{\mathsf {pkecorr}}_{\mathsf {PKE}}(\mathcal {C}) = 0\) for all (even computationally unbounded) adversaries \(\mathcal {C}\). See Sect. 4 for discussion on game-based definitions of correctness.
Define the min-entropy of algorithms \(\mathsf {\mathsf {PKE}.Kg}\) and \(\mathsf {\mathsf {PKE}.Enc}\) as \(\mathrm {H}_{\infty }(\mathsf {\mathsf {PKE}.Kg})\) and \(\mathrm {H}_{\infty }(\mathsf {\mathsf {PKE}.Enc})\), respectively, defined as follows:

The probability is defined over the random coins used by \(\mathsf {\mathsf {PKE}.Kg}\) and \(\mathsf {\mathsf {PKE}.Enc}\), respectively. Note that min-entropy does not depend on the output values  (in the former case) and
(in the former case) and  (in the latter case).
(in the latter case).
\({\underline{\textsf {Ciphertext\, indistinguishability\, under\, exposures.}}}\) Consider game \(\mathrm {INDEXP}\) of Fig. 3, associated to a key-updating public-key encryption scheme \(\mathsf {PKE}\) and an adversary \(\mathcal {A}_{\mathsf {PKE}}\). Roughly, it requires that \(\mathsf {PKE}\) maintain CCA security [3] even if \(\mathcal {A}_{\mathsf {PKE}}\) is given the decryption key (as long as that decryption key is no longer able to decrypt any challenge ciphertexts).
The adversary \(\mathcal {A}_{\mathsf {PKE}}\) can call the oracle \(\textsc {NewUser}\) arbitrarily many times with a user identifier \(\varLambda \) and be given the encryption key of that user. Then it can interact with user \(\varLambda \) via four oracles. Via calls to \(\textsc {Enc}\) with messages  and label \(\ell \) it requests that one of these messages be encrypted using the specified label (which message is encrypted depends on the secret bit b). It will be given back the new encryption key and the produced ciphertext. If
and label \(\ell \) it requests that one of these messages be encrypted using the specified label (which message is encrypted depends on the secret bit b). It will be given back the new encryption key and the produced ciphertext. If  we remember that a challenge query was done.
we remember that a challenge query was done.
Via calls to \(\textsc {Dec}\) with ciphertext  and \(\ell \) it requests that the ciphertext be decrypted with the specified label. Adversary \(\mathcal {A}_{\mathsf {PKE}}\) will only be given the result of this decryption if the pair
and \(\ell \) it requests that the ciphertext be decrypted with the specified label. Adversary \(\mathcal {A}_{\mathsf {PKE}}\) will only be given the result of this decryption if the pair  was not obtained from a call to \(\textsc {Enc}\). Once the adversary queries such pair, the user \(\varLambda \) becomes “restricted” and the oracle will return the true decryption of all future ciphertexts for this user.
was not obtained from a call to \(\textsc {Enc}\). Once the adversary queries such pair, the user \(\varLambda \) becomes “restricted” and the oracle will return the true decryption of all future ciphertexts for this user.
Via calls to \(\textsc {ExpRand}\) it asks to be given the next randomness that will be used for encryption. This represents the adversary exposing the randomness while the encryption is taking place so we require that after a call to \(\textsc {ExpRand}\) the adversary immediately makes the corresponding call to \(\textsc {Enc}\). During this call challenges are forbidden so it must choose  .
.
Via calls to \(\textsc {ExpDk}\) it asks to be given the current decryption key of the user. It may not do so if a challenge query was done but the user has not decrypted the corresponding ciphertext yet (unless the user is restricted). Otherwise the decryption key is returned and the user is considered to be exposed. Once a user is exposed challenges are not allowed so for all future calls to \(\textsc {Enc}\) the adversary required to choose  .
.
At the end of the game the adversary outputs a bit \(b'\) representing its guess of the secret bit b. The advantage of \(\mathcal {A}_{\mathsf {PKE}}\) in breaking the \(\mathrm {INDEXP}\) security of \(\mathsf {PKE}\) is defined as \(\mathsf {Adv}^{\mathsf {indexp}}_{\mathsf {PKE}}(\mathcal {A}_{\mathsf {PKE}}) = 2 \Pr [\mathrm {INDEXP}^{\mathcal {A}_{\mathsf {PKE}}}_{\mathsf {PKE}}] - 1\).
Many of the variables used to track the behavior of the adversary in \(\mathrm {INDEXP}\) are analogous to variables we use and discuss in detail in Sect. 5 when defining security of a channel. The reader interested in understand the pseudocode of \(\mathrm {INDEXP}\) in detail is encouraged to read that section first.
\({\underline{\textsf {Construction.}}}\) In [27] we use a hierarchical identity-based encryption (HIBE) scheme to construct a secure key-updating encryption scheme. Roughly, a HIBE assigns a decryption key to any identity (vector of strings). A decryption key for an identity \({\varvec{I}}\) can be used to create decryption keys for an identity of which \({\varvec{I}}\) is a prefix. Security requires that the adversary be unable to learn about encrypted messages encrypted to an identity \({\varvec{I}}\) even if given the decryption key for many identities as long as none of them were prefixes of \({\varvec{I}}\). To create a key-updating encryption scheme we use the vector of ciphertexts and labels a user has received so far as the identity. The security of this scheme then follows from the security of the underlying HIBE in a fairly straightforward manner.
4 Bidirectional Cryptographic Channels
In this section we formally define the syntax and correctness of bidirectional cryptographic channels. Our notion of bidirectional channels will closely match that of Marson and Poettering [30]. Compared to their definition, we allow the receiving algorithm to be randomized and provide an alternative correctness condition. We argue that the new correctness condition is more appropriate for our desired use case of secure messaging. Henceforth, we will omit the adjective “bidirectional” and refer simply to channels.
\({\underline{\textsf {Syntax\, of\, channel.}}}\) A channel provides a method for two users to exchange messages in an arbitrary order. We will refer to the two users of a channel as the initiator \(\mathcal {I}\) and the receiver \(\mathcal {R}\). There will be no formal distinction between the two users, but when specifying attacks we follow the convention of having \(\mathcal {I}\) send a ciphertext first. We will use  as a variable to represent an arbitrary user and
as a variable to represent an arbitrary user and  to represent the other user. More formally, when
to represent the other user. More formally, when  we let
we let  denote the sole element of
denote the sole element of  .
.
A channel \(\mathsf {Ch}\) specifies algorithms \(\mathsf {\mathsf {Ch}.Init}\), \(\mathsf {\mathsf {Ch}.Send}\), and \(\mathsf {\mathsf {Ch}.Recv}\). Initialization algorithm \(\mathsf {\mathsf {Ch}.Init}\) returns initial states  and
and  , where
, where  is \(\mathcal {I}\)’s state and
is \(\mathcal {I}\)’s state and  is \(\mathcal {R}\)’s state. We write
is \(\mathcal {R}\)’s state. We write  . Sending algorithm \(\mathsf {\mathsf {Ch}.Send}\) takes state
. Sending algorithm \(\mathsf {\mathsf {Ch}.Send}\) takes state  , associated data
, associated data  , and message
, and message  to return updated state
to return updated state  and a ciphertext
and a ciphertext  . We write
. We write  . Receiving algorithm takes state
. Receiving algorithm takes state  , associated data
, associated data  , and ciphertext
, and ciphertext  to return updated state
to return updated state  and message
and message  . We write
. We write  , where
, where  represents a rejection of ciphertext
represents a rejection of ciphertext  and
and  represents the channel being permanently shut down from the perspective of
represents the channel being permanently shut down from the perspective of  (recall our convention regarding \(\bot \) as input to an algorithm). One notion of correctness we discuss will require that
(recall our convention regarding \(\bot \) as input to an algorithm). One notion of correctness we discuss will require that  whenever
whenever  . The other will require that
. The other will require that  not be changed from its input value when
not be changed from its input value when  .
.
We let \(\mathsf {\mathsf {Ch}.InitRS}\), \(\mathsf {\mathsf {Ch}.SendRS}\), and \(\mathsf {\mathsf {Ch}.RecvRS}\) denote the sets of possible random coins for \(\mathsf {\mathsf {Ch}.Init}\), \(\mathsf {\mathsf {Ch}.Send}\), and \(\mathsf {\mathsf {Ch}.Recv}\), respectively. Note that for full generality we allow \(\mathsf {\mathsf {Ch}.Recv}\) to be randomized. Prior work commonly requires this algorithm to be deterministic.
Games defining correctness of channel \(\mathsf {Ch}\). Lines labelled with the name of a game are included only in that game. \(\mathrm {CORR}\) requires that \(\mathsf {Ch}\) be robust when given an incorrect ciphertext via oracle \(\textsc {Robust}\). \(\mathrm {CORR\bot }\) requires that \(\mathsf {Ch}\) permanently returns \(\bot \) when given an incorrect ciphertext via oracle \(\textsc {Reject}\).
\({\underline{\textsf {Correctness\, of\, channel.}}}\) In Fig. 4 we provide two games, defining two alternative correctness requirements for a cryptographic channel. Lines labelled with the name of a game are included only in that game. The games differ in whether the adversary is given access to an oracle \(\textsc {Robust}\) or to an oracle \(\textsc {Reject}\). Game \(\mathrm {CORR}\) uses the former, whereas game \(\mathrm {CORR\bot }\) uses the latter. The advantage of an adversary \(\mathcal {C}\) against the correctness of channel \(\mathsf {Ch}\) is given by \(\mathsf {Adv}^{\mathsf {corr}}_{\mathsf {Ch}}(\mathcal {C})=\Pr [\mathrm {CORR}^{\mathcal {C}}_{\mathsf {Ch}}]\) in one case, and \(\mathsf {Adv}^{\mathsf {corr\bot }}_{\mathsf {Ch}}(\mathcal {C})=\Pr [\mathrm {CORR\bot }^{\mathcal {C}}_{\mathsf {Ch}}]\) in the other case. Correctness with respect to either notion requires that the advantage is equal 0 for all (even computationally unbounded) adversaries \(\mathcal {C}\).
Our use of games to define correctness conditions follows the work of Marson and Poettering [30] and Bellare et. al. [7]. By considering unbounded adversaries and requiring an advantage of 0 we capture a typical information-theoretic perfect correctness requirement without having to explicitly quantify over sequences of actions. In this work we require only the perfect correctness because it is achieved by our scheme; however, it would be possible to capture computational correctness by considering a restricted class of adversaries.
Both games require that ciphertexts sent by any user are always decrypted to the correct message by the other user. This is modeled by providing adversary \(\mathcal {C}\) with access to oracles \(\textsc {Send}\) and \(\textsc {Recv}\). We assume that messages from  to
to  are received in the same order they were sent, and likewise that messages from
are received in the same order they were sent, and likewise that messages from  to
to  are also received in the correct order (regardless Aof how they are interwoven on both sides, since ciphertexts are being sent in both directions).
are also received in the correct order (regardless Aof how they are interwoven on both sides, since ciphertexts are being sent in both directions).
The games differ in how the channel is required to behave in the case that a ciphertext is rejected. Game \(\mathrm {CORR}\) (using oracle \(\textsc {Robust}\)) requires that the state of the user not be changed so that the channel can continue to be used. Game \(\mathrm {CORR\bot }\) (using oracle \(\textsc {Reject}\)) requires that the state of the user is set to \(\bot \). According to our conventions about the behavior of algorithms given \(\bot \) as input (see Sect. 2), the channel will then refuse to perform any further actions by setting all subsequent outputs to \(\bot \). We emphasize that the adversary specifies all inputs to \(\mathsf {\mathsf {Ch}.Recv}\) when making calls to \(\textsc {Robust}\) and \(\textsc {Reject}\), so the behavior of those oracles is not related to the behavior of the other two oracles for which the game maintains the state of both users.
\({\underline{\textsf {Comparison\, of\, correctness\, notions.}}}\) The correctness required by \(\mathrm {CORR\bot }\) is identical to that of Marson and Poettering [30]. The \(\mathrm {CORR}\) notion of correctness instead uses a form of robustness analogous to that of [7]. In [27] we discuss how these correctness notions have different implications for the security of the channel. It is trivial to convert a \(\mathrm {CORR}\)-correct channel to a \(\mathrm {CORR\bot }\)-correct channel and vice versa. Thus we will, without loss of generality, only provide a scheme achieving \(\mathrm {CORR}\)-correctness.
5 Security Notion for Channels
In this section we will define what it means for a channel to be secure in the presence of a strong attacker that can steal the secrets of either party in the communication. Our goal is to give the strongest possible notion of security in this setting, encompassing both the privacy of messages and the integrity of ciphertexts. We take a fine-grained look at what attacks are possible and require that a channel be secure against all attacks that are not syntactically inherent in the definition of a channel.
To introduce our security notion we will first describe a simple interface of how the adversary is allowed to interact with the channel. Then we show attacks that would break the security of any channel using this interface. Our final security notion will be created by adding checks to the interface that prevents adversary from performing any sequence of actions that leads to these unpreventable breaches of security. We introduce only the minimal necessary restrictions preventing the attacks, making sure that we allow all adversaries that do not trivially break the security as per above.
5.1 Channel Interface Game
Consider game \(\mathrm {INTER}\) in Fig. 5. It defines the interface between an adversary \(\mathcal {D}\) and a channel \(\mathsf {Ch}\). A secret bit b is chosen at random and the adversary’s goal is to guess this bit given access to a left-or-right sending oracle, real-or-\(\bot \) receiving oracle, and an exposure oracle. The sending oracle takes as input a user  , two messages
, two messages  , and associated data
, and associated data  . Then it returns the encryption of
. Then it returns the encryption of  with
with  by user
by user  . The receiving oracle \(\textsc {Recv}\) takes as input a user
. The receiving oracle \(\textsc {Recv}\) takes as input a user  , a ciphertext
, a ciphertext  , and associated data
, and associated data  . It has user
. It has user  decrypt this ciphertext using
decrypt this ciphertext using  , and proceeds as follows. If \(b=0\) holds (along with another condition we discuss momentarily) then it returns the valid decryption of this ciphertext; otherwise it returns \(\bot \). The exposure oracle \(\textsc {Exp}\) takes as input a user
, and proceeds as follows. If \(b=0\) holds (along with another condition we discuss momentarily) then it returns the valid decryption of this ciphertext; otherwise it returns \(\bot \). The exposure oracle \(\textsc {Exp}\) takes as input a user  , and a flag \(\mathsf {rand}\). It returns user’s state
, and a flag \(\mathsf {rand}\). It returns user’s state  , and it might return random coins that will be used the next time this user runs algorithms \(\mathsf {\mathsf {Ch}.Send}\) or \(\mathsf {\mathsf {Ch}.Recv}\) (depending on the value of \(\mathsf {rand}\), which we discuss below). The advantage of adversary \(\mathcal {D}\) against channel \(\mathsf {Ch}\) is defined by \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D})=2\Pr [\mathrm {INTER}^{\mathcal {D}}_{\mathsf {Ch}}]-1\).
, and it might return random coins that will be used the next time this user runs algorithms \(\mathsf {\mathsf {Ch}.Send}\) or \(\mathsf {\mathsf {Ch}.Recv}\) (depending on the value of \(\mathsf {rand}\), which we discuss below). The advantage of adversary \(\mathcal {D}\) against channel \(\mathsf {Ch}\) is defined by \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D})=2\Pr [\mathrm {INTER}^{\mathcal {D}}_{\mathsf {Ch}}]-1\).
This interface gives the adversary full control over the communication between the two users of the channel. It may modify, reorder, or block any communication as it sees fit. The adversary is able to exfiltrate the secret state of either party at any time.
Let us consider the different cases of how a user’s secrets might be exposed. They could be exposed while the user is in the middle of performing a \(\mathsf {\mathsf {Ch}.Send}\) operation, in the middle of performing a \(\mathsf {\mathsf {Ch}.Recv}\) operation, or when the user is idle (i.e. not in the middle of performing \(\mathsf {\mathsf {Ch}.Send}\) or \(\mathsf {\mathsf {Ch}.Recv}\)). In the last case we expect the adversary to learn the user’s state  , but nothing else. If the adversary is exposing the user during an operation, they would potentially learn the state before the operation, any secrets computed during the operation, and the state after the operation. We capture this by leaking the state from before the operation along with the randomness that will be used when the adversary makes its next query to \(\textsc {Send}\) or \(\textsc {Recv}\). This allows the adversary to compute the next state as well. The three possible values of \(\mathsf {rand}\) are \(\mathsf {rand}=\) “send” for the first possibility, \(\mathsf {rand}=\) “recv” for the second possibility, and \(\mathsf {rand}=\varepsilon \) for the third. These exposures represent what the adversary is learning while a particular operation is occurring, so we require (via \(\mathsf {nextop}\)) that after such an exposure it immediately makes the corresponding oracle query. Without the use of the exposure oracle the game specified by this interface would essentially be equivalent to the combination of the integrity and confidentiality security notions defined by Marson and Poettering [30] in the all-in-one definition style of Rogaway and Shrimpton [37].
, but nothing else. If the adversary is exposing the user during an operation, they would potentially learn the state before the operation, any secrets computed during the operation, and the state after the operation. We capture this by leaking the state from before the operation along with the randomness that will be used when the adversary makes its next query to \(\textsc {Send}\) or \(\textsc {Recv}\). This allows the adversary to compute the next state as well. The three possible values of \(\mathsf {rand}\) are \(\mathsf {rand}=\) “send” for the first possibility, \(\mathsf {rand}=\) “recv” for the second possibility, and \(\mathsf {rand}=\varepsilon \) for the third. These exposures represent what the adversary is learning while a particular operation is occurring, so we require (via \(\mathsf {nextop}\)) that after such an exposure it immediately makes the corresponding oracle query. Without the use of the exposure oracle the game specified by this interface would essentially be equivalent to the combination of the integrity and confidentiality security notions defined by Marson and Poettering [30] in the all-in-one definition style of Rogaway and Shrimpton [37].
The interface game already includes some standard checks. First, we require that on any query  to \(\textsc {Send}\) the adversary must provide equal length messages. If the adversary does not do so (i.e.
to \(\textsc {Send}\) the adversary must provide equal length messages. If the adversary does not do so (i.e.  ) then \(\textsc {Send}\) returns \(\bot \) immediately. This prevents the inherent attack where an adversary could distinguish between the two values of b by asking for encryptions of different length messages and checking the length of the output ciphertext. Adversary \(\mathcal {D}_1\) in Fig. 6 does just that and would achieve \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_1) > 1/2\) against any channel \(\mathsf {Ch}\) if not for that check.
) then \(\textsc {Send}\) returns \(\bot \) immediately. This prevents the inherent attack where an adversary could distinguish between the two values of b by asking for encryptions of different length messages and checking the length of the output ciphertext. Adversary \(\mathcal {D}_1\) in Fig. 6 does just that and would achieve \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_1) > 1/2\) against any channel \(\mathsf {Ch}\) if not for that check.
Second, we want to prevent \(\textsc {Recv}\) from decrypting ciphertexts that are simply forwarded to it from \(\textsc {Send}\). So for each user  we keep track of counters
we keep track of counters  and
and  that track how many messages that user has sent and received. Then at the end of a \(\textsc {Send}\) call to
that track how many messages that user has sent and received. Then at the end of a \(\textsc {Send}\) call to  the ciphertext-associated data pair
the ciphertext-associated data pair  is stored in the table
is stored in the table  with index
with index  . When \(\textsc {Recv}\) is called for user
. When \(\textsc {Recv}\) is called for user  it will compare the pair
it will compare the pair  against
against  and if the pair matches return \(\bot \) regardless of the value of the secret bit. If we did not do this check then for any channel \(\mathsf {Ch}\) the adversary \(\mathcal {D}_2\) shown in Fig. 6 would achieve \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_2)=1\).
and if the pair matches return \(\bot \) regardless of the value of the secret bit. If we did not do this check then for any channel \(\mathsf {Ch}\) the adversary \(\mathcal {D}_2\) shown in Fig. 6 would achieve \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_2)=1\).
We now specify several efficient adversaries that will have high advantage for any choice of  . For concreteness we always have our adversaries immediately start the actions required to perform the attacks, but all of the attacks would still work if the adversary had performed a number of unrelated procedure calls first. Associated data will never be important for our attacks so we will always set it to \(\varepsilon \). We will typically set
. For concreteness we always have our adversaries immediately start the actions required to perform the attacks, but all of the attacks would still work if the adversary had performed a number of unrelated procedure calls first. Associated data will never be important for our attacks so we will always set it to \(\varepsilon \). We will typically set  and
and  . For the following we let \(\mathsf {Ch}\) be any channel and consider the adversaries shown in Fig. 6.
. For the following we let \(\mathsf {Ch}\) be any channel and consider the adversaries shown in Fig. 6.
\({\underline{\textsf {Trivial\, Forgery.}}}\) If the adversary exposes the secrets of  it will be able to forge a ciphertext that
it will be able to forge a ciphertext that  would accept at least until the future point in time when
would accept at least until the future point in time when  has received the ciphertext that
has received the ciphertext that  creates next. For a simple example of this consider the third adversary, \(\mathcal {D}_3\). It exposes the secrets of user \(\mathcal {I}\), then uses them to perform its own \(\mathsf {\mathsf {Ch}.Send}\) computation locally, and sends the resulting ciphertext to \(\mathcal {R}\). Clearly this ciphertext will always decrypt to a non-\(\bot \) value so the adversary can trivially determine the value of b and achieve \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_3)=1\).
creates next. For a simple example of this consider the third adversary, \(\mathcal {D}_3\). It exposes the secrets of user \(\mathcal {I}\), then uses them to perform its own \(\mathsf {\mathsf {Ch}.Send}\) computation locally, and sends the resulting ciphertext to \(\mathcal {R}\). Clearly this ciphertext will always decrypt to a non-\(\bot \) value so the adversary can trivially determine the value of b and achieve \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_3)=1\).
After an adversary has done the above to trivially send a forgery to  it can easily perform further attacks on both the integrity and authenticity of the channel. These are shown by adversaries \(\mathcal {D}_{3.1}\) and \(\mathcal {D}_{3.2}\). The first displays the fact that the attacker can easily send further forgeries to
it can easily perform further attacks on both the integrity and authenticity of the channel. These are shown by adversaries \(\mathcal {D}_{3.1}\) and \(\mathcal {D}_{3.2}\). The first displays the fact that the attacker can easily send further forgeries to  . The second displays the fact that the attacker can now easily decrypt any messages sent by
. The second displays the fact that the attacker can now easily decrypt any messages sent by  . We have \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_{3.1})=1\) and \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_{3.2})=1\).
. We have \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_{3.1})=1\) and \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_{3.2})=1\).
\({\underline{\textsf {Trivial\, Challenges.}}}\) If the adversary exposes the secrets of  it will necessarily be able to decrypt any ciphertexts already encrypted by
it will necessarily be able to decrypt any ciphertexts already encrypted by  that have not already been received by
that have not already been received by  . Consider the adversary \(\mathcal {D}_4\). It determines what message was encrypted by user \(\mathcal {I}\) by exposing the state of \(\mathcal {R}\), and uses that to run \(\mathsf {\mathsf {Ch}.Recv}\). We have \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_4)=1\).
. Consider the adversary \(\mathcal {D}_4\). It determines what message was encrypted by user \(\mathcal {I}\) by exposing the state of \(\mathcal {R}\), and uses that to run \(\mathsf {\mathsf {Ch}.Recv}\). We have \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_4)=1\).
Similarly, if the adversary exposes the secrets of  it will necessarily be able to decrypt any future ciphertexts encrypted by
it will necessarily be able to decrypt any future ciphertexts encrypted by  , until
, until  receives the ciphertext that
receives the ciphertext that  creates next. Consider the adversary \(\mathcal {D}_5\). It is essentially the identical to adversary \(\mathcal {D}_4\), except it reverses the order of the calls made to \(\textsc {Send}\) and \(\textsc {Exp}\). We have \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_5)=1\).
creates next. Consider the adversary \(\mathcal {D}_5\). It is essentially the identical to adversary \(\mathcal {D}_4\), except it reverses the order of the calls made to \(\textsc {Send}\) and \(\textsc {Exp}\). We have \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_5)=1\).
\({\underline{\textsf {Exposing\, Randomness.}}}\) If an adversary exposes user  with \(\mathsf {rand}=\) “send” then it is able to compute the next state of
with \(\mathsf {rand}=\) “send” then it is able to compute the next state of  by running \(\mathsf {\mathsf {Ch}.Send}\) locally with the same randomness that
by running \(\mathsf {\mathsf {Ch}.Send}\) locally with the same randomness that  will use. So in this case the security game must act as if the adversary exposed both the current and the next state. In particular, the attacks above could only succeed until, first, the exposed user
will use. So in this case the security game must act as if the adversary exposed both the current and the next state. In particular, the attacks above could only succeed until, first, the exposed user  updated its secrets and, second, user
updated its secrets and, second, user  updates its secrets accordingly (which can happen after it receives the next message from
updates its secrets accordingly (which can happen after it receives the next message from  ). But if the randomness was exposed, then secrets would need to be updated at least twice until the security is restored.
). But if the randomness was exposed, then secrets would need to be updated at least twice until the security is restored.
Exposing user  with \(\mathsf {rand}=\) “send” additionally allows the attack shown in \(\mathcal {D}_6\). The adversary exposes the state and the sending randomness of \(\mathcal {I}\), encrypts 1 locally using these exposed values of \(\mathcal {I}\), and then calls \(\textsc {Send}\) to get a challenge ciphertext sent by \(\mathcal {I}\). The adversary compares whether the two ciphertexts are the same to determine the secret bit. We have \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_6)=1\). More broadly, if the adversary exposes the secrets of
with \(\mathsf {rand}=\) “send” additionally allows the attack shown in \(\mathcal {D}_6\). The adversary exposes the state and the sending randomness of \(\mathcal {I}\), encrypts 1 locally using these exposed values of \(\mathcal {I}\), and then calls \(\textsc {Send}\) to get a challenge ciphertext sent by \(\mathcal {I}\). The adversary compares whether the two ciphertexts are the same to determine the secret bit. We have \(\mathsf {Adv}^{\mathsf {inter}}_{\mathsf {Ch}}(\mathcal {D}_6)=1\). More broadly, if the adversary exposes the secrets of  with \(\mathsf {rand}=\) “send” it will always be able to tell what is the next message encrypted by
with \(\mathsf {rand}=\) “send” it will always be able to tell what is the next message encrypted by  .
.
Exposing with \(\mathsf {rand}=\) “recv” does not generically endow the adversary with the ability to do any additional attacks.
5.2 Optimal Security of a Channel
Our full security game is obtained by adding a minimal amount of code to \(\mathrm {INTER}\) to disallow the generic attacks just discussed. Consider the game \(\mathrm {AEAC}\) (authenticated encryption against compromise) shown in Fig. 7. We define the advantage of an adversary \(\mathcal {D}\) against channel \(\mathsf {Ch}\) by \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {Ch}}(\mathcal {D})=2\Pr [\mathrm {AEAC}^{\mathcal {D}}_{\mathsf {Ch}}]-1\).
We now have a total of eight variables to control the behavior of the adversary and prevent it from abusing trivial attacks. Some of the variables are summarized in Fig. 8. We have already seen  ,
,  , \(\mathsf {nextop}\), and
, \(\mathsf {nextop}\), and  in \(\mathrm {INTER}\). The new variables we have added in \(\mathrm {AEAC}\) are tables
in \(\mathrm {INTER}\). The new variables we have added in \(\mathrm {AEAC}\) are tables  and
and  , number
, number  , and flag
, and flag  . We now discuss the new variables.
. We now discuss the new variables.
The table  was added to prevent the type of attack shown in \(\mathcal {D}_3\). When the adversary calls \(\textsc {Exp}\) on user
was added to prevent the type of attack shown in \(\mathcal {D}_3\). When the adversary calls \(\textsc {Exp}\) on user  we set
we set  to \(\text {``trivial''}\) for the indices of ciphertexts for which this adversary is now necessarily able to create forgeries. If the adversary takes advantage of this to send a ciphertext of its own creation to
to \(\text {``trivial''}\) for the indices of ciphertexts for which this adversary is now necessarily able to create forgeries. If the adversary takes advantage of this to send a ciphertext of its own creation to  then the flag
then the flag  will be set, whose effect we will describe momentarily.
will be set, whose effect we will describe momentarily.
The table  is used to prevent the types of attacks shown by \(\mathcal {D}_4\) and \(\mathcal {D}_6\). Whenever the adversary makes a valid challenge queryFootnote 2 to user
is used to prevent the types of attacks shown by \(\mathcal {D}_4\) and \(\mathcal {D}_6\). Whenever the adversary makes a valid challenge queryFootnote 2 to user  we set
we set  to \(\text {``done''}\). The game will not allow the adversary to expose
to \(\text {``done''}\). The game will not allow the adversary to expose  ’s secrets if there are any challenge queries for which
’s secrets if there are any challenge queries for which  sent a ciphertext that
sent a ciphertext that  has not received yet. This use of
has not received yet. This use of  prevents an attack like \(\mathcal {D}_4\). To prevent an attack like \(\mathcal {D}_6\), we set
prevents an attack like \(\mathcal {D}_4\). To prevent an attack like \(\mathcal {D}_6\), we set  to \(\text {``forbidden''}\) whenever the adversary exposes the state and sending randomness of
to \(\text {``forbidden''}\) whenever the adversary exposes the state and sending randomness of  . This disallows the adversary from doing a challenge query during its next \(\textsc {Send}\) call to
. This disallows the adversary from doing a challenge query during its next \(\textsc {Send}\) call to  (the call for which the adversary knows the corresponding randomness).
(the call for which the adversary knows the corresponding randomness).
The number  prevents attacks like \(\mathcal {D}_5\). When
prevents attacks like \(\mathcal {D}_5\). When  is exposed
is exposed  will be set to a number that is 1 or 2 greater than the current number of ciphertexts
will be set to a number that is 1 or 2 greater than the current number of ciphertexts  has sent (depending on the value of \(\mathsf {rand}\)) and challenge queries from
has sent (depending on the value of \(\mathsf {rand}\)) and challenge queries from  will not be allowed until it has received that many ciphertexts. This ensures that the challenge queries from
will not be allowed until it has received that many ciphertexts. This ensures that the challenge queries from  are not issued with respect to exposed keys of
are not issued with respect to exposed keys of  .Footnote 3
.Footnote 3
Finally the flag  serves to both allow and disallow some attacks. The flag is initialized to \(\mathsf {false}\). It is set to \(\mathsf {true}\) when the adversary forges a ciphertext to
serves to both allow and disallow some attacks. The flag is initialized to \(\mathsf {false}\). It is set to \(\mathsf {true}\) when the adversary forges a ciphertext to  after exposing
after exposing  . Once
. Once  has received a different ciphertext than was sent by
has received a different ciphertext than was sent by  there is no reason to think that
there is no reason to think that  should be able to decrypt ciphertexts sent by
should be able to decrypt ciphertexts sent by  or send its own ciphertexts to
or send its own ciphertexts to  . As such, if
. As such, if  is restricted (i.e.
is restricted (i.e.  ) we will not add its ciphertexts to
) we will not add its ciphertexts to  , we will always show the true output when
, we will always show the true output when  attempts to decrypt ciphertexts given to it by the adversary (even if they were sent by
attempts to decrypt ciphertexts given to it by the adversary (even if they were sent by  ), and if the adversary asks to expose
), and if the adversary asks to expose  we will return all of its secret state without setting any of the other variables that would restrict the actions the adversary is allowed to take.
we will return all of its secret state without setting any of the other variables that would restrict the actions the adversary is allowed to take.
The above describes how  allows some attacks. Now we discuss how it prevents attacks like \(\mathcal {D}_{3.1}\) and \(\mathcal {D}_{3.2}\). Once the adversary has sent its own ciphertext to
allows some attacks. Now we discuss how it prevents attacks like \(\mathcal {D}_{3.1}\) and \(\mathcal {D}_{3.2}\). Once the adversary has sent its own ciphertext to  we must assume that the adversary will be able to decrypt ciphertexts sent by
we must assume that the adversary will be able to decrypt ciphertexts sent by  and able to send its own ciphertexts to
and able to send its own ciphertexts to  that will decrypt to non-\(\bot \) values. The adversary could simply have “replaced”
that will decrypt to non-\(\bot \) values. The adversary could simply have “replaced”  with itself. To address this we prevent all challenge queries from
with itself. To address this we prevent all challenge queries from  , and decryptions performed by
, and decryptions performed by  are always given back to the adversary regardless of the secret bit.
are always given back to the adversary regardless of the secret bit.
\({\underline{\textsf {Informal\, description\, of\, the\, security\, game.}}}\) In [27] we provide a thorough written description of our security model to facilitate high-level understanding of it. For intricate security definitions like ours there is often ambiguity or inconsistency in subtle corner cases of the definition when written out fully in text. As such this description should merely be considered an informal aid while the pseudocode of Fig. 7 is the actual definition.
\({\underline{\textsf {Comparison\, to\, recent\, definitions.}}}\) The three recents works we studied while deciding how to write our security definition were [7, 14, 26]. Their settings were all distinct, but each presented security models that involve different “stages” of keys. All three works made distinct decisions in how to address challenges in different stages. In [27] we discuss these decisions, noting that they result in qualitatively identical but quantitatively distinct definitions.
6 Construction of a Secure Channel
6.1 Our Construction
We are not aware of any secure channels that would meet (or could easily be modified to meet) our security notion. The “closest” (for some unspecified, informal notion of distance) is probably the Signal Double Ratchet Algorithm. However, it relies on symmetric authenticated encryption for both privacy and integrity so it is inherently incapable of achieving our strong notion of security. Later, we describe an attack against a variant of our proposed construction that uses symmetric primitives to exhibit the sorts of attacks that are unavoidable when using them. A straightforward variant of this attack would also apply against the Double Ratchet Algorithm.
In this section we construct our cryptographic channel and motivate our design decisions by giving attacks against variants of the channel. In Sect. 6.2 we will prove its security by reducing it to that of its underlying components.
The idea of our scheme is as follows. Both parties will keep track of a transcript of the messages they have sent and received,  and
and  . These will be included as a part of every ciphertext and verified before a ciphertext is accepted. On seeing a new ciphertext the appropriate transcript is updated to be the hash of the ciphertext (note that the old transcript is part of this ciphertext, so the transcript serves as a record of the entire conversation). Sending transcripts (vector of
. These will be included as a part of every ciphertext and verified before a ciphertext is accepted. On seeing a new ciphertext the appropriate transcript is updated to be the hash of the ciphertext (note that the old transcript is part of this ciphertext, so the transcript serves as a record of the entire conversation). Sending transcripts (vector of  ) are stored until the other party has acknowledged receiving a more recent transcript.
) are stored until the other party has acknowledged receiving a more recent transcript.
For authenticity, every time a user sends a ciphertext they authenticate it with a digital signature and include in it the verification key for the signing key that they will use to sign the next ciphertext they send. Any time a user receives a ciphertext they will use the new receiving transcript produced to update their current signing key.
For privacy, messages will be encrypted using public-key encryption. With every ciphertext the sender will include the encryption key for a new decryption key they have generated. Decryption keys are stored until the other party has acknowledged receiving a more recent encryption key. The encryption will use as a label all of the extra data that will be included with the ciphertext (i.e. a sending counter, a receiving counter, an associated data string, a new verification key, a new encryption key, a receiving transcript, and a sending transcript). The formal definition of our channel is as follows.
\({\underline{\textsf {Cryptographic\, channel\, SCH[DS, PKE, H].}}}\) Let \(\mathsf {DS}\) be a key-updatable digital signature scheme, \(\mathsf {PKE}\) be a key-updating public-key encryption scheme, and \(\mathsf {H}\) be a family of functions. We build a cryptographic channel \(\mathsf {SCh}=\mathsf {SCH}[\mathsf {DS},\mathsf {PKE},\mathsf {H}]\) as defined in Fig. 9.
A user’s state  , among other values, contains counters
, among other values, contains counters  . Here,
. Here,  is the number of messages that
is the number of messages that  sent to
sent to  , and
, and  is the number of messages they received back from
is the number of messages they received back from  . The counter
. The counter  stores the last value of
stores the last value of  in a ciphertext received by
in a ciphertext received by  (i.e. the index of the last ciphertext that
(i.e. the index of the last ciphertext that  believes
believes  has received and acknowledged). This counter is used to ensure that prior to running a signature verification algorithm, the verification key
has received and acknowledged). This counter is used to ensure that prior to running a signature verification algorithm, the verification key  is updated with respect to the same transcripts as the signing key
is updated with respect to the same transcripts as the signing key  (at the time it was used to produce the signature). Note that algorithm \(\mathsf {\mathsf {DS}.Vrfy}\) returns
(at the time it was used to produce the signature). Note that algorithm \(\mathsf {\mathsf {DS}.Vrfy}\) returns  where t is the result of verifying that \(\sigma \) is a valid signature for v with respect to verification key
where t is the result of verifying that \(\sigma \) is a valid signature for v with respect to verification key  (using the notation convention from Sect. 3).
(using the notation convention from Sect. 3).
\({\underline{\textsf {Inefficiencies of SCh.}}}\) A few aspects of \(\mathsf {SCh}\) are less efficient than one would a priori hope. The state maintained by a user  (specifically the tables
(specifically the tables  and
and  ) is not constant in size, but instead grows linearly with the number of ciphertexts that
) is not constant in size, but instead grows linearly with the number of ciphertexts that  sent to
sent to  without receiving a reply back. Additionally, when \(\mathsf {DS}\) is instantiated with the particular choice of \(\mathsf {DS}\) that we define in [27] the length of the ciphertext sent by a user
without receiving a reply back. Additionally, when \(\mathsf {DS}\) is instantiated with the particular choice of \(\mathsf {DS}\) that we define in [27] the length of the ciphertext sent by a user  will grow linearly in the number of ciphertexts that
will grow linearly in the number of ciphertexts that  has received since the last time they sent a ciphertext. When \(\mathsf {PKE}\) is instantiated with the scheme we define in [27] there is an extra state being stored that is linear in the number of ciphertexts that
has received since the last time they sent a ciphertext. When \(\mathsf {PKE}\) is instantiated with the scheme we define in [27] there is an extra state being stored that is linear in the number of ciphertexts that  has sent since it last received a ciphertext. Such inefficiencies would be unacceptable for a protocol like TLS or SSH, but in our motivating context of messaging is it plausible that they are acceptable. Each message is human generated and the state gets “refreshed” regularly if the two users regularly reply to one another. One could additionally consider designing an app to regularly send an empty message whose sole purpose is state refreshing. We leave as interesting future work improving on the efficiency of our construction.
has sent since it last received a ciphertext. Such inefficiencies would be unacceptable for a protocol like TLS or SSH, but in our motivating context of messaging is it plausible that they are acceptable. Each message is human generated and the state gets “refreshed” regularly if the two users regularly reply to one another. One could additionally consider designing an app to regularly send an empty message whose sole purpose is state refreshing. We leave as interesting future work improving on the efficiency of our construction.
\({\underline{\textsf {Design\, decisions.}}}\) We will now discuss attacks against different variants of \(\mathsf {SCh}\). This serves to motivate the decisions made in its design and give intuition for why it achieves the desired security. Several steps in the security proof of this construction can be understood by noting which of these attacks are ruled out in the process.
The attacks are shown in Figs. 10 and 11. The first several attacks serve to demonstrate that \(\mathsf {\mathsf {Ch}.Send}\) must use a sufficient amount of randomness (shown in \(\mathcal {D}_a\), \(\mathcal {D}_b\), \(\mathcal {D}_c\)) and that \(\mathsf {H}\) needs to be collision resistant (shown in \(\mathcal {D}_b\), \(\mathcal {D}_c\)). The next attack shows why our construction would be insecure if we did not use labels with \(\mathsf {PKE}\) (shown in \(\mathcal {D}_d\)). Then we provide two attacks showing why the keys of \(\mathsf {DS}\) and \(\mathsf {PKE}\) need to be updated (shown in \(\mathcal {D}_e\), \(\mathcal {D}_f\)). Then we show an attack that arises if multiple valid signatures can be found for the same string (shown in \(\mathcal {D}_g\)). Finally, we conclude with attacks that would apply if we used symmetric instead of asymmetric primitives to build \(\mathsf {SCh}\) (shown in \(\mathcal {D}_h\), \(\mathcal {D}_i\)).
\({\underline{\textsf {Scheme\, with\, insufficient\, sending \,entropy.}}}\) Any scheme whose sending algorithm has insufficient entropy will necessarily be insecure. For simplicity let \(\mathsf {SCh}_1\) be a variant of \(\mathsf {SCh}\) such that \(\mathsf {\mathsf {SCh}_1.Send}\) is deterministic (the details of how we are making it deterministic do not matter). We can attack both the message privacy and the integrity of such a scheme.
Consider the adversary \(\mathcal {D}_a\). It exposes \(\mathcal {I}\), encrypts the message 1 locally, and then sends a challenge query to \(\mathcal {I}\) asking for the encryption of either 1 or 0. By comparing the ciphertext it produced to the one returned by \(\textsc {Send}\) it can determine which message was encrypted, learning the secret bit. We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_1}(\mathcal {D}_a)=1\). This attack is fairly straightforward and will be ruled out by the security of \(\mathsf {PKE}\) in our proof without having to be addressed directly.
The attacks against integrity are more subtle. They are explicitly addressed in the first game transition of our proof. Let \(\mathsf {Ch}=\mathsf {SCh}_1\) and consider adversaries \(\mathcal {D}_b\) and \(\mathcal {D}_c\). They both start by doing the same sequence of operations: expose \(\mathcal {I}\), use its secret state to encrypt and send message 1 to \(\mathcal {R}\), then ask \(\mathcal {I}\) to produce an encryption of 1 for \(\mathcal {R}\) (which will be the same ciphertext as above, because \(\mathsf {\mathsf {SCh}_1.Send}\) is deterministic). Now \({\mathsf {restricted}}_{\mathcal {R}}=\mathsf {true}\) because oracle \(\textsc {Recv}\) was called on a trivially fogeable ciphertext that was not produced by oralce \(\textsc {Send}\). But \(\mathcal {R}\) has received the exact same ciphertext that \(\mathcal {I}\) sent. Different attacks are possible from this point.
Adversary \(\mathcal {D}_b\) just asks \(\mathcal {R}\) to send a message and forwards it along to \(\mathcal {I}\). Since \(\mathcal {R}\) was restricted the ciphertext does not get added to \(\mathbf {ctable}_{\mathcal {I}}\) so it can be used to discover the secret bit. We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_1}(\mathcal {D}_b)=1\). Adversary \(\mathcal {D}_c\) exposes \(\mathcal {R}\) and uses the state it obtains to create its own forgery to \(\mathcal {I}\). It then returns 1 or 0 depending on whether \(\textsc {Recv}\) returns the correct decryption or \(\bot \). This attack succeeds because exposing \(\mathcal {R}\) when it is restricted will not set any of the variables that would typically prevent the adversary from winning by creating a forgery. We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_1}(\mathcal {D}_c)=1\). We have not shown it, but another message privacy attack at this point (instead of proceeding as \(\mathcal {D}_b\) or \(\mathcal {D}_c\)) could have asked for another challenge query from \(\mathcal {I}\), exposed \(\mathcal {R}\), and used the exposed state to trivially determine which message was encrypted.
\({\underline{\textsf {Scheme\, without\, collision-resistant\, hashing.}}}\) If it is easy to find collisions in \(\mathsf {H}\) then we can attack the channel by causing both parties to have matching transcripts despite having seen different sequences of ciphertexts. For concreteness let \(\mathsf {SCh}_2\) be a variant of our scheme using a hash function that outputs \(0^{128}\) on all inputs. Let \(\mathsf {Ch}=\mathsf {SCh}_2\) and again consider adversaries \(\mathcal {D}_b\) and \(\mathcal {D}_c\). We no longer expect the ciphertexts that they produce locally to match the ciphertexts returned by \(\mathcal {I}\). However, they will have the same hash value and thus produce the same transcript  . Consequently, \(\mathcal {R}\) still updates its signing key in the same way regardless of whether it receives the ciphertext produced by \(\mathcal {I}\) or the ciphertext locally generated by adversary. So the messages subsequently sent by \(\mathcal {R}\) will still be accepted by \(\mathcal {I}\). We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_2}(\mathcal {D}_b)=1\) and \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_2}(\mathcal {D}_c)=1\).
. Consequently, \(\mathcal {R}\) still updates its signing key in the same way regardless of whether it receives the ciphertext produced by \(\mathcal {I}\) or the ciphertext locally generated by adversary. So the messages subsequently sent by \(\mathcal {R}\) will still be accepted by \(\mathcal {I}\). We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_2}(\mathcal {D}_b)=1\) and \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_2}(\mathcal {D}_c)=1\).
\({\underline{\textsf {Scheme\, without\, PKE \,labels.}}}\) Let \(\mathsf {SCh}_3\) be a variant of \(\mathsf {SCh}\) that uses a public-key encryption scheme that does not accept labels and consider adversary \(\mathcal {D}_d\). It exposes \(\mathcal {I}\) and asks \(\mathcal {I}\) for a challenge query. It then uses the state it exposed to trivially modify the ciphertext sent from \(\mathcal {I}\) (we chose to have it change  from \(\varepsilon \) to \(1^{128}\)) and sends it to \(\mathcal {R}\). Since the ciphertext sent to \(\mathcal {R}\) has different associated data than the one sent by \(\mathcal {I}\) the adversary will be given the decryption of this ciphertext. But without the use of labels this decryption by \(\mathsf {PKE}\) is independent of the associated data and will thus reveal the true decryption of the challenge ciphertext to \(\mathcal {I}\). We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_3}(\mathcal {D}_d)=1\).
from \(\varepsilon \) to \(1^{128}\)) and sends it to \(\mathcal {R}\). Since the ciphertext sent to \(\mathcal {R}\) has different associated data than the one sent by \(\mathcal {I}\) the adversary will be given the decryption of this ciphertext. But without the use of labels this decryption by \(\mathsf {PKE}\) is independent of the associated data and will thus reveal the true decryption of the challenge ciphertext to \(\mathcal {I}\). We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_3}(\mathcal {D}_d)=1\).
\({\underline{\textsf {Schemes \,without\, key\, updating.}}}\) We will now show why it is necessary to define new forms of \(\mathsf {PKE}\) and \(\mathsf {DS}\) for our construction.
Let \(\mathsf {SCh}_4\) be a variant of \(\mathsf {SCh}\) that uses a digital signature scheme that does not update its keys. Consider adversary \(\mathcal {D}_e\). It exposes \(\mathcal {I}\), then queries \(\textsc {Send}\) for \(\mathcal {I}\) to send a message to \(\mathcal {R}\), but uses the exposed secrets to replace it with a locally produced ciphertext  . It calls \(\textsc {Recv}\) for \(\mathcal {R}\) with
. It calls \(\textsc {Recv}\) for \(\mathcal {R}\) with  , which sets \({\mathsf {restricted}}_{\mathcal {R}}=\mathsf {true}\). Since the signing key is not updated in \(\mathsf {SCh}_4\), the adversary now exposes \(\mathcal {R}\) to obtain a signing key whose signatures will be accepted by \(\mathcal {I}\). It uses this to forge a ciphertext to \(\mathcal {I}\) to learn the secret bit. We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_4}(\mathcal {D}_e)=1\).
, which sets \({\mathsf {restricted}}_{\mathcal {R}}=\mathsf {true}\). Since the signing key is not updated in \(\mathsf {SCh}_4\), the adversary now exposes \(\mathcal {R}\) to obtain a signing key whose signatures will be accepted by \(\mathcal {I}\). It uses this to forge a ciphertext to \(\mathcal {I}\) to learn the secret bit. We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_4}(\mathcal {D}_e)=1\).
Let \(\mathsf {SCh}_5\) be a variant of \(\mathsf {SCh}\) that uses a public-key encryption scheme that does not update its keys. Consider adversary \(\mathcal {D}_f\). It exposes \(\mathcal {I}\) and uses this to send \(\mathcal {R}\) a different ciphertext than is sent by \(\mathcal {I}\) (setting \({\mathsf {restricted}}_{\mathcal {R}}=\mathsf {true}\)). Since the decryption key is not updated, the adversary now exposes \(\mathcal {R}\) to obtain a decryption key that can be used to decrypt a challenge ciphertext sent by \(\mathcal {I}\). We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_5}(\mathcal {D}_f)=1\).
\({\underline{\textsf {Scheme\, with\, non-unique\, signatures.}}}\) Let \(\mathsf {SCh}_6\) be a variant of our scheme using a digital signature scheme that does not have unique signatures. For concreteness, assume that  is a valid signature whenever \(\sigma \) is. Then consider adversary \(\mathcal {D}_g\). It exposes \(\mathcal {I}\) and has \(\mathcal {I}\) send a challenge ciphertext. Then it modifies the ciphertext by changing the signature and forwards this modified ciphertext on to \(\mathcal {R}\). The adversary is given back the true decryption of this ciphertext (because it was changed) which trivially reveals the secret bit of the game (here it is important that the signature is not part of the label used for encryption/decryption). We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_6}(\mathcal {D}_g)=1\).
is a valid signature whenever \(\sigma \) is. Then consider adversary \(\mathcal {D}_g\). It exposes \(\mathcal {I}\) and has \(\mathcal {I}\) send a challenge ciphertext. Then it modifies the ciphertext by changing the signature and forwards this modified ciphertext on to \(\mathcal {R}\). The adversary is given back the true decryption of this ciphertext (because it was changed) which trivially reveals the secret bit of the game (here it is important that the signature is not part of the label used for encryption/decryption). We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_6}(\mathcal {D}_g)=1\).
\({\underline{\textsf {Scheme\, with\, symmetric\, primitives.}}}\) Let \(\mathsf {SCh}_7\) be a variant of our scheme that uses a MAC instead of a digital signature scheme (e.g.  always, and
always, and  is presumably no longer sent in the clear with the ciphertext). Consider adversary \(\mathcal {D}_h\). It simply exposes \(\mathcal {I}\) and then uses \(\mathcal {I}\)’s
is presumably no longer sent in the clear with the ciphertext). Consider adversary \(\mathcal {D}_h\). It simply exposes \(\mathcal {I}\) and then uses \(\mathcal {I}\)’s  to send a message to \(\mathcal {I}\). This trivially allows it to determine the secret bit. Here we used that \(\mathsf {PKE}\) will decrypt any ciphertext to a non-\(\bot \) value. We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_7}(\mathcal {D}_h)=1\).
to send a message to \(\mathcal {I}\). This trivially allows it to determine the secret bit. Here we used that \(\mathsf {PKE}\) will decrypt any ciphertext to a non-\(\bot \) value. We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_7}(\mathcal {D}_h)=1\).
Similarly let \(\mathsf {SCh}_8\) be a variant of our scheme that uses symmetric encryption instead of public-key encryption (e.g.  always, and
always, and  is presumably no longer sent in the clear with the ciphertext). Adversary \(\mathcal {D}_i\) exposes user \(\mathcal {I}\) and then uses the corresponding
is presumably no longer sent in the clear with the ciphertext). Adversary \(\mathcal {D}_i\) exposes user \(\mathcal {I}\) and then uses the corresponding  to decrypt a challenge message encrypted by \(\mathcal {I}\). We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_8}(\mathcal {D}_i)=1\).
to decrypt a challenge message encrypted by \(\mathcal {I}\). We have \(\mathsf {Adv}^{\mathsf {aeac}}_{\mathsf {SCh}_8}(\mathcal {D}_i)=1\).
Stated broadly, a scheme that relies on symmetric primitives will not be secure because a user will know sufficient information to send a ciphertext that they would themselves accept or to read a message that they sent to the other user. Our security notion requires that this is not possible.
6.2 Security Theorem
The following theorem bounds the advantage of an adversary breaking the \(\mathrm {AEAC}\) security of \(\mathsf {SCh}\) using the advantages of adversaries against the \(\mathrm {CR}\) security of \(\mathsf {H}\), the \(\mathrm {UFEXP}\) and \(\mathrm {UNIQ}\) security of \(\mathsf {DS}\), the \(\mathrm {INDEXP}\) security of \(\mathsf {PKE}\), and the min-entropy of \(\mathsf {DS}\) and \(\mathsf {PKE}\).
Theorem 1
Let \(\mathsf {DS}\) be a key-updatable digital signature scheme, \(\mathsf {PKE}\) be a key-updating public-key encryption scheme, and \(\mathsf {H}\) be a family of functions. Let \(\mathsf {SCh}=\mathsf {SCH}[\mathsf {DS},\mathsf {PKE},\mathsf {H}]\). Let \(\mathcal {D}\) be an adversary making at most \(q_{\textsc {Send}}\) queries to its \(\textsc {Send}\) oracle, \(q_{\textsc {Recv}}\) queries to its \(\textsc {Recv}\) oracle, and \(q_{\textsc {Exp}}\) queries to its \(\textsc {Exp}\) oracle. Then we can build adversaries \(\mathcal {A}_{\mathsf {H}}\), \(\mathcal {A}_{\mathsf {DS}}\), \(\mathcal {B}_{\mathsf {DS}}\), and \(\mathcal {A}_{\mathsf {PKE}}\) such that
where \(\mu =\mathrm {H}_{\infty }(\mathsf {\mathsf {DS}.Kg})+\mathrm {H}_{\infty }(\mathsf {PKE.Kg})+\mathrm {H}_{\infty }(\mathsf {\mathsf {PKE}.Enc})\). Adversary \(\mathcal {A}_{\mathsf {DS}}\) makes at most \(q_{\textsc {Send}}+2\) queries to its \(\textsc {NewUser}\) oracle, \(q_{\textsc {Send}}\) queries to its \(\textsc {Sign}\) oracle, and \(q_{\textsc {Exp}}\) queries to its \(\textsc {Exp}\) oracle. Adversary \(\mathcal {B}_{\mathsf {DS}}\) makes at most \(q_{\textsc {Send}}+2\) queries to its \(\textsc {NewUser}\) oracle. Adversary \(\mathcal {A}_{\mathsf {PKE}}\) makes at most \(q_{\textsc {Send}}+2\) queries to its \(\textsc {NewUser}\) oracle, \(q_{\textsc {Send}}\) queries to its \(\textsc {Enc}\) oracle, \(q_{\textsc {Recv}}\) queries to its \(\textsc {Dec}\) oracle, \(q_{\textsc {Send}}+2\) queries to its \(\textsc {ExpDk}\) oracle, and \(\min \{q_{\textsc {Exp}},q_{\textsc {Send}}+1\}\) queries to its \(\textsc {ExpRand}\) oracle. Adversaries \(\mathcal {A}_{\mathsf {H}}\), \(\mathcal {A}_{\mathsf {DS}}\), \(\mathcal {B}_{\mathsf {DS}}\), and \(\mathcal {A}_{\mathsf {PKE}}\) all have runtime about that of \(\mathcal {D}\).
The proof is in [27]. It broadly consists of two stages. The first stage of the proof (consisting of three game transitions) argues that the adversary will not be able to forge a ciphertext to an unrestricted user except by exposing the other user. This argument is justified by a reduction to an adversary \(\mathcal {A}_{\mathsf {DS}}\) against the security of the digital signature scheme. However, care must be taken in this reduction to ensure that \(\mathcal {D}\) cannot induce behavior in \(\mathcal {A}_{\mathsf {DS}}\) that would result in \(\mathcal {A}_{\mathsf {DS}}\) cheating in the digital signature game. Addressing this possibility involves arguing that \(\mathcal {D}\) cannot predict any output of \(\textsc {Send}\) (from whence the min-entropy term in the bound arises) and that it cannot find any collisions in the hash function \(\mathsf {H}\).
Once this stage is complete the output of \(\textsc {Recv}\) no longer depends on the secret bit b, so we move to using the security of \(\mathsf {PKE}\) to argue that \(\mathcal {D}\) cannot use \(\textsc {Send}\) to learn the value of the secret bit. This is the second stage of the proof. But prior to this reduction we have to make one last argument using the security of \(\mathsf {DS}\). Specifically we show that, given a ciphertext \((\sigma ,v)\), the adversary will not be able to find a new signature \(\sigma '\) such that \((\sigma ',v)\) will be accepted by the receiver (otherwise since \(\sigma \ne \sigma '\), oracle \(\textsc {Recv}\) would return the true decryption of this ciphertext which would be the same as the decryption of the original ciphertext and thus allow a trivial attack). Having done this, the reduction to the security of \(\mathsf {PKE}\) is straightforward.
Notes
- 1.
We are thus defining security for a one-time signature scheme, because a particular key will only be used for one signature. This is all we require for our application, but the definition and construction we provide could easily be extended to allow multiple signatures if desired.
- 2.
We use the term challenge query to refer to a \(\textsc {Send}\) query for which
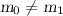 .
. - 3.
The symbol chi is meant to evoke the word “challenge” because it stores the next time the adversary may make a challenge query.
References
Bellare, M., Boldyreva, A., Micali, S.: Public-key encryption in a multi-user setting: security proofs and improvements. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 259–274. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_18
Bellare, M., Desai, A., Jokipii, E., Rogaway, P.: A concrete security treatment of symmetric encryption. In: FOCS 1997 (1997)
Bellare, M., Desai, A., Pointcheval, D., Rogaway, P.: Relations among notions of security for public-key encryption schemes. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 26–45. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055718
Bellare, M., Kohno, T., Namprempre, C.: Breaking and provably repairing the ssh authenticated encryption scheme: a case study of the encode-then-encrypt-and-mac paradigm. ACM Trans. Inf. Syst. Secur. (TISSEC) 7(2), 206–241 (2004)
Bellare, M., Miner, S.K.: A forward-secure digital signature scheme. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 431–448. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_28
Bellare, M., Rogaway, P.: The security of triple encryption and a framework for code-based game-playing proofs. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 409–426. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_25
Bellare, M., Singh, A.C., Jaeger, J., Nyayapati, M., Stepanovs, I.: Ratcheted encryption and key exchange: the security of messaging. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10403, pp. 619–650. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_21
Bellare, M., Yee, B.: Forward-security in private-key cryptography. In: Joye, M. (ed.) CT-RSA 2003. LNCS, vol. 2612, pp. 1–18. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36563-X_1
Boldyreva, A., Degabriele, J.P., Paterson, K.G., Stam, M.: Security of symmetric encryption in the presence of ciphertext fragmentation. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 682–699. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_40
Borisov, N., Goldberg, I., Brewer, E.: Off-the-record communication, or, why not to use PGP. In: ACM Workshop on Privacy in the Electronic Society (2004)
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: FOCS 2001 (2001)
Canetti, R., Halevi, S., Katz, J.: A forward-secure public-key encryption scheme. J. Cryptol. 20(3), 265–294 (2007)
Canetti, R., Krawczyk, H.: Analysis of key-exchange protocols and their use for building secure channels. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 453–474. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_28
Cohn-Gordon, K., Cremers, C., Dowling, B., Garratt, L., Stebila, D.: A formal security analysis of the Signal messaging protocol. In: Proceedings of IEEE European Symposium on Security and Privacy (EuroS&P) (2017)
Cohn-Gordon, K., Cremers, C., Garratt, L.: On post-compromise security. In: IEEE Computer Security Foundations Symposium (CSF) (2016)
Desmedt, Y., Frankel, Y.: Threshold cryptosystems. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 307–315. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_28
Diffie, W., van Oorschot, P.C., Wiener, M.J.: Authentication and authenticated key exchanges. Des. Codes Crypt. 2(2), 107–125 (1992)
Dodis, Y., Katz, J., Xu, S., Yung, M.: Key-insulated public key cryptosystems. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 65–82. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_5
Dodis, Y., Katz, J., Xu, S., Yung, M.: Strong key-insulated signature schemes. In: Desmedt, Y.G. (ed.) PKC 2003. LNCS, vol. 2567, pp. 130–144. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36288-6_10
Dodis, Y., Luo, W., Xu, S., Yung, M.: Key-insulated symmetric key cryptography and mitigating attacks against cryptographic cloud software. In: ASIACCS 2012 (2012)
Perrin, T. (ed.), Marlinspike, M.: The double ratchet algorithm, 20 November 2016. https://whispersystems.org/docs/specifications/doubleratchet/
Fischlin, M., Günther, F., Marson, G.A., Paterson, K.G.: Data is a stream: security of stream-based channels. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 545–564. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_27
Gentry, C., Silverberg, A.: Hierarchical ID-based cryptography. In: Zheng, Y. (ed.) ASIACRYPT 2002. LNCS, vol. 2501, pp. 548–566. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-36178-2_34
Green, M.D., Miers, I.: Forward secure asynchronous messaging from puncturable encryption. In: IEEE Symposium on Security and Privacy (2015)
Günther, C.G.: An identity-based key-exchange protocol. In: Quisquater, J.-J., Vandewalle, J. (eds.) EUROCRYPT 1989. LNCS, vol. 434, pp. 29–37. Springer, Heidelberg (1990). https://doi.org/10.1007/3-540-46885-4_5
Günther, F., Mazaheri, S.: A formal treatment of multi-key channels. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10403, pp. 587–618. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_20
Jaeger, J., Stepanovs, I.: Optimal Channel Security Against Fine-Grained State Compromise: The Safety of Messaging. Cryptology ePrint Archive, Report 2018/XYZ (2018, To appear)
Krawczyk, H.: The order of encryption and authentication for protecting communications (or: how secure is SSL?). In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 310–331. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_19
Langley, A.: Pond. GitHub repository, README.md (2012). https://github.com/agl/pond/commit/7bb06244b9aa121d367a6d556867992d1481f0c8
Marson, G.A., Poettering, B.: Security notions for bidirectional channels. IACR Trans. Symm. Cryptol. 2017(1), 405–426 (2017)
Mignotte, M.: How to share a secret? In: Beth, T. (ed.) EUROCRYPT 1982. LNCS, vol. 149, pp. 371–375. Springer, Heidelberg (1983). https://doi.org/10.1007/3-540-39466-4_27
Namprempre, C.: Secure channels based on authenticated encryption schemes: a simple characterization. In: Zheng, Y. (ed.) ASIACRYPT 2002. LNCS, vol. 2501, pp. 515–532. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-36178-2_32
Open Whisper Systems. Signal protocol library for Java/Android. GitHub repository (2017). https://github.com/WhisperSystems/libsignal-protocol-java
Ostrovsky, R., Yung, M.: How to withstand mobile virus attacks (extended abstract). In: ACM PODC 1991 (1991)
Poettering, B., Rösler, P.: Ratcheted key exchange, revisited. Cryptology ePrint Archive, Report 2018/296 (2018). https://eprint.iacr.org/2018/296
Rogaway, P.: Authenticated-encryption with associated-data. In: ACM CCS 2002 (2002)
Rogaway, P., Shrimpton, T.: A provable-security treatment of the key-wrap problem. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 373–390. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_23
Shamir, A.: How to share a secret. Commun. Assoc. Comput. Mach. 22(11), 612–613 (1979)
Shoup, V.: On formal models for secure key exchange. Cryptology ePrint Archive, Report 1999/012 (1999). http://eprint.iacr.org/1999/012
Shoup, V.: A proposal for an ISO standard for public key encryption. Cryptology ePrint Archive, Report 2001/112 (2001). https://eprint.iacr.org/2001/112
Tompa, M., Woll, H.: How to share a secret with cheaters. J. Cryptol. 1(2), 133–138 (1988)
Unger, N., Dechand, S., Bonneau, J., Fahl, S., Perl, H., Goldberg, I., Smith, M.: SoK: secure messaging. In: IEEE Symposium on Security and Privacy (2015)
WhatsApp Blog. Connecting one billion users every day, 26 July 2017. https://blog.whatsapp.com/10000631/Connecting-One-Billion-Users-Every-Day
Acknowledgments
We thank Mihir Bellare for extensive discussion on preliminary versions of this paper. We thank the CRYPTO 2018 reviewers for their comments. Jaeger and Stepanovs were supported in part by NSF grants CNS-1717640 and CNS-1526801.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Jaeger, J., Stepanovs, I. (2018). Optimal Channel Security Against Fine-Grained State Compromise: The Safety of Messaging. In: Shacham, H., Boldyreva, A. (eds) Advances in Cryptology – CRYPTO 2018. CRYPTO 2018. Lecture Notes in Computer Science(), vol 10991. Springer, Cham. https://doi.org/10.1007/978-3-319-96884-1_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-96884-1_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96883-4
Online ISBN: 978-3-319-96884-1
eBook Packages: Computer ScienceComputer Science (R0)















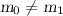 .
.