Keywords

1 Introduction

Natural disasters always have been one of the human concerns. The statistics show that between 1980 and 2004 two million people were killed and 5 billion people affected by natural disasters in total [1]. To solve the problems encountered during natural disasters, various people and organizations such as local and International Humanitarian Organizations (IHO), government and military get involved in helping the injured [2, 3]. Meanwhile, the benevolent people are also willing to contribute to solving the problems by providing different kinds of donations. This cooperation alongside its various benefits, can increases the complexity of coordination and implementation of disaster relief programs, especially when donations be unsolicited [2, 4]. This unrequested supplies and donations can cause troubles such as waste relief teams’ time, resources, congest the relief chain and create bottlenecks [5]. On the other hand, previous researches have emphasized the role of media attention on increasing these issues [2, 3]. It has been explained that increasing media attention will increase unsolicited donations and consequently, the problems created for relief teams will be intensified [2]. Also, it is completely significant for donors to perceive that their donations are used in a way that has the greatest possible benefit for the injured [2]. In fact, donors are somehow the customers of relief organizations and thereupon, they must be satisfied to continue their co-operation [4]. Besides, it is proven that the media’s attention, especially online social networks, can be used as a powerful platform to attract more donations [4, 6]. For example, After the Haiti earthquake during 48 h Red Cross received around 8 million dollars of charity through people’s texts in social media [7].

The role and importance of social media in attracting help and donations in one side and the obstacles of receiving undemand aids on the other hand, highlights the need for managing and directing the media attention in the event of natural disasters. This research aims to propose a method for influencer selection, using the Social Network Analysis (SNA) and optimization techniques, through which it would be possible to establish an adaptation between the public attention in social media and the type of injured necessities. In this way, current research would come up with a solution to prevent mentioned problems in relief programs. In this paper, Influencer refers to individuals who have some personal or network desirable attributes such as expertise, credibility, and connectivity enabling them to persuade people in their network [8]. Influencers can shape others attitudes by their power of authenticity and reach [9].

2 Social Media in Disaster Relief Management

With the development of online social networks, a variety of applications of these networks for disaster relief management also are emerged. Crisis management organizations, are using data extracted from social networks to determine where aid are needed and to broadcast their own needs [10]. As instance, Ushahidi (www.Ushahidi.com) is an open source platform providing crisis map to show the different needs of injured by their locations [7]. A great deal of research has been made in this regard. A survey showed that Twitter activity after a hurricane has a strong correlation with per-capita economic damages, and it suggested that the online social networks could be used for rapid assessment of damage caused by a large-scale natural disaster [11]. Based on Zhu et al. (2011) the understanding of the factors that influence the behavior of Twitter users in retweeting tweets on natural disasters will make it easier for disaster managers to choose optimal messages to propagate in the network. In other words, they focused on how to choose the best content to speed up the information propounding the disaster to help injured [12]. In a comprehensive review, Landwehr et al. (2014) divided the social network analysis and efforts in crisis management into four categories, keyword-based labeling, crowdsourcing-based labeling, sentiment based labeling and network analysis for relevance [10]. Based on literature analysis, the social media have been considered as an influential channel to engage people and donors in crisis management during natural disasters.

3 Method

In order to develop a method for influencer selection, using the Social Network Analysis (SNA) and optimization techniques to choose the best set of influencers in a complex network is necessary. In this way, an adaption between actual injured needs and public awareness of each kind of the needs through an online social network would be possible. This will be done in three subsections: in the first step, the diffusion model of a message through a social network is discussed. In the second subsection, our subject is differentiated from a typical influence maximization problem and then the problem is formulated to obtain the cost function. And finally in the last section, the optimization algorithm to make the adaptation is applied.

3.1 Diffusion Model

As discussed, a social network can be a powerful tool for spreading information among individuals. So far, many scholars have studied the information diffusion model in a social network [13], including researches on the diffusion process in “word of mouth” [14] and “viral marketing” [15]. Influence maximization is also considered as an attractive topic of research in the marketing field, which researchers are trying to maximize the distribution of a message on a network by finding the most influential nodes [16,17,18,19]. Meanwhile, David Kempe et al. (2003) formulated this issue by presenting two stochastic diffusion models [17], which have become a basis for many researchers in this field [16]. In this paper, one of Kempe et al. (2003) diffusion models, called Independent Cascade, is used as the basis for our model.

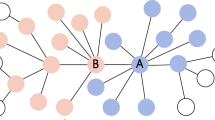
Let’s assume G = (N, E) as a directed social network where N represents the set of nodes (individuals) and E represents set of edges (relationships between individuals). In this network, each node is considered as being active or inactive (active nodes have received the message). Now we start with a set of initial active nodes A0. In the first step t = 0 each active node like V has a single chance to activate its inactive neighbor W, with probability PVW. At the end of this step if any of the active nodes succeed to activate any of its neighbors, diffusion process will continue in the step t = 1 with the set of newly activated nodes A1,, otherwise the entire diffusion process model will be stopped. It should be noted that in this case, each node could only activate the neighbors who follow him (followers), and can be activated by his neighbors whom he follows (following). Therefore, it is necessary to consider the direction of the edges. For example in Fig. 1, node V can be activated by node Y with probability PYV and can activate node W and U respectively with probability PVW and PVU.

Fig. 1.
figure 1

A sample graph with 4 nodes

Full size image

In this paper, a real data set of 347 friends on Facebook is utilized to test and run algorithms. This data set is free and available on www.snap.stanford.edu/data.

3.2 Formulating Problem

Again, let’s assume G = (N, E) as our network where \( N = \left( {\begin{array}{*{20}c} {n_{1} } & \cdots & {n_{i} } \\ \end{array} } \right) \) represents set of nodes. In this network, each node like Y can activate all other nodes in t steps with different probabilities. For example in Fig. 1, Y can activate W in two steps with probability PYW = PYV.PVW. In this way, matrix GP illustrates the chance of each node to activate any other one.

$$ G_{P} = \begin{array}{*{20}c} {n_{1} } \\ {n_{2} } \\ \vdots \\ {n_{i} } \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} {n_{1 } \quad } & { n_{2} } & { \cdots } & {n_{i } } \\ \end{array} } \\ {\left[ {\begin{array}{*{20}c} {P_{{n_{1} n_{1} }} } & {P_{{n_{1} n_{2} }} } & \cdots & {P_{{n_{1} n_{i} }} } \\ {P_{{n_{2} n_{1} }} } & {P_{{n_{2} n_{2} }} } & {} & {P_{{n_{2} n_{i} }} } \\ \vdots & {} & \ddots & \vdots \\ {P_{{n_{i} n_{1} }} } & {P_{{n_{i} n_{2} }} } & \cdots & {P_{{n_{i} n_{i} }} } \\ \end{array} } \right]} \\ \end{array} $$
(1)

Figure 2 represents an example of the probability of activating other nodes by initially activated node n56 in the network of Facebook friends.

Fig. 2.
figure 2

Influence of sample node “n56”

Full size image

Now we need to consider set \( A = \left( {\begin{array}{*{20}c} {a_{1} } & \cdots & {a_{j} } \\ \end{array} } \right) \) as set of different needs of injured (items), and \( V = \left( {\begin{array}{*{20}c} {v_{1} } & \cdots & {v_{j} } \\ \end{array} } \right) \) as set of the volume of each item, which is estimated by relief teams.

The objective is to select a set of influencers S in such a way that the level of awareness of each item through the network be adapted to the volume of actual needs.

$$ S = \left( {\begin{array}{*{20}c} {n_{{a_{1} }} } & {n_{{a_{2} }} } & \cdots & {n_{{a_{j} }} } \\ \end{array} } \right) $$
(2)

In above set of influencers, each element like \( n_{{a_{1} }} \), represents the influencer who is in charge for influence item \( a_{1} \). As argued, each influencer (each node) can activate all other nodes, so it is considered that there is a possibility for all nodes to donate any item. Matrix GA represents this issue:

$$ G_{A} = \begin{array}{*{20}c} {n_{{a_{1} }} } \\ {n_{{a_{2} }} } \\ \vdots \\ {n_{{a_{j} }} } \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} {n_{1} \quad } & {n_{2} } & \cdots & {n_{i} } \\ \end{array} } \\ {\left[ {\begin{array}{*{20}c} {P_{{n_{{a_{1} }} n_{1} }} } & {P_{{n_{{a_{1} }} n_{2} }} } & \cdots & {P_{{n_{{a_{1} }} n_{i} }} } \\ {P_{{n_{{a_{2} }} n_{1} }} } & {P_{{n_{{a_{2} }} n_{2} }} } & {} & {P_{{n_{{a_{2} }} n_{i} }} } \\ \vdots & {} & \ddots & \vdots \\ {P_{{n_{{a_{j} }} n_{1} }} } & {P_{{n_{{a_{j} }} n_{2} }} } & \cdots & {P_{{n_{{a_{j} }} n_{i} }} } \\ \end{array} } \right]} \\ \end{array} \quad , \; j \le i $$
(3)

In above matrix, \( P_{{n_{{a_{1} }} n_{1} }} \) is the probability for \( n_{1} \) to be activated by \( n_{{a_{1} }} \) regardless to the presence of other influencers. But \( n_{1} \) can be activated by other influencers as well. It means that the influence boundaries of influencers may overlap in some nodes. So, the probability that \( n_{1} \) will be going to donate \( a_{1} \) in presence of other influencers, is calculated as below:

$$ P_{{a_{1} n_{1} }} = P_{{\left( {n_{1 } \,be{\kern 1pt} {\kern 1pt} activated} \right)}} .P_{{\left( {n_{1 } \,{\kern 1pt} choose{\kern 1pt} a_{1} } \right)}} $$
(4)
$$ P_{{\left( {n_{1 } {\kern 1pt} {\kern 1pt} be{\kern 1pt} {\kern 1pt} activated} \right)}} = 1 - \prod \left( {1 - P_{{n_{{a_{j} }} n_{1} }} } \right) $$
(5)
$$ P_{{\left( {n_{1 } {\kern 1pt} {\kern 1pt} choose{\kern 1pt} {\kern 1pt} a_{1} } \right)}} = \frac{{P_{{n_{{a_{1} }} n_{1} }} }}{{\sum P_{{n_{{a_{j} }} n_{1} }} }} $$
(6)

By repeating the above for all nodes, it is possible to calculate the probability for each node who will donate \( a_{1} \) in presence of other influencers. These calculations can be again repeated for other items to obtain matrix GD.

$$ GD = \begin{array}{*{20}c} {a_{1} } \\ {a_{2} } \\ \vdots \\ {a_{j} } \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} {n_{1} \quad } & {n_{2} } & \cdots & {n_{i} } \\ \end{array} } \\ {\left[ {\begin{array}{*{20}c} {P_{{a_{1} n_{1} }} } & {P_{{a_{1} n_{2} }} } & \cdots & {P_{{a_{1} n_{i} }} } \\ {P_{{a_{2} n_{1} }} } & {P_{{a_{2} n_{2} }} } & {} & {P_{{a_{2} n_{i} }} } \\ \vdots & {} & \ddots & \vdots \\ {P_{{a_{j} n_{1} }} } & {P_{{a_{j} n_{2} }} } & \cdots & {P_{{a_{j} n_{i} }} } \\ \end{array} } \right]} \\ \end{array} \quad , \;j \le i $$
(7)
$$ P_{{\left( {Total {\kern 1pt} probability \,of\,donating\, a_{j} } \right)}} = \mathop \sum \limits_{1}^{i} P_{{a_{j} n_{i} }} $$
(8)

To clarify the difference between this matrix and the previous one, it should be noted that in the previous matrix the effect of the presence of other influencers was not taken into account. So any change in influencer set S may cause a change in all elements of the matrix GD and consequently change in total probability for donating all items. Therefore, it is complicated to choose the best set of influencers in such a way that total probability of donating different needs in the network, adapt to the actual volume of each item. This issue necessitates deploying optimization algorithms in the next section.

3.3 Optimization Algorithm

The first step to solve an optimization problem is calculating the cost function. The cost function is defined as the distance from the current state to the optimal condition. Therefore, the more this function gets closer to zero, the more favorable the situation is. In this case, the favorable situation is the equality of the actual amount of demand per item with the total probability of donating that item. So, the cost function is as below:

$$ CostFunction : \mathop \sum \limits_{1}^{j} \left| {v_{j} - \mathop \sum \limits_{1}^{i} P_{{a_{j} n_{i} }} } \right| $$
(9)

In above function, \( V = \left( {\begin{array}{*{20}c} {v_{1} } & \cdots & {v_{j} } \\ \end{array} } \right) \) is the actual needed amount of each item, which is estimated by the relief teams. Now by employing an optimization algorithm, we can find the best set of influencers to minimize the difference between the actual need of an item and total probability for donating that item (minimizing cost function).

3.4 Quantum Genetic Algorithm (QGA)

This study deployed an evolutionary Genetic Algorithm, QGA, which is based on quantum computing and quantum theory concepts to minimize the cost function. Researchers have already shown a variety of positive features for this algorithm, including low computing time, powerful search capability and fast convergence [20].

Considering the complexity of the network of Facebook friends and the fact that the ID of the nodes in the dataset does not follow a particular order, which made the network more complicated, this algorithm, QGA, is used for optimization. For the initial random population, after several trials and errors, we have chosen 50 chromosomes and 100 iterations as it leads the results to an acceptable level of convergence and efficiency. Each chromosome contains 5 genes, which in this case represents a set of 5 influencers. So, each gen can get an integer number between 1 and 347 (Population).

4 Results

As explained, in solving influencer maximization problems, researchers are trying to select the most influential set of influencers, whereas, this research intended to solve another type of problem. Therefore, the result of this study is compared with two other methods of selecting the influencers. The first method is simple random selection, which can be considered as the result of decision making without having the network information (Random Selection). In the second method, the criteria for selecting influencers are the influential power of the individuals in the absence of the other influencers. It means that if we need the awareness of item a1 to be v1, we will simply choose the node with influential power equal to v1 (Fast Selection).

To compare the result of the methods, a set of 5 needs as \( V = \left( {\begin{array}{*{20}c} {10} & {\begin{array}{*{20}c} {30} & {14} & {23} \\ \end{array} } & 8 \\ \end{array} } \right) \) is considered for the population of network = 347. So, 22.7% of the network needs to get activated, tailored to the needs. In Table 1, the results of the proposed method is compared with two other ones. We repeated QGA selection method 100 times to get better results and also to check the reliability of this method. Additionally, for the random selection method, 100 different sets of influencers have been chosen randomly. But regarding the fast selection method, only one set of influencers, which is the closest set based on the influential power to the set of injured needs V, was picked up.

Table 1. Results
Full size table

In Table 1, the term Efficiency shows how much a method is successful to make the adaption between the awareness in the network and the set of injured necessities and is calculated as below:

$$ Efficiency : 1 - \frac{Cost}{{\mathop \sum \nolimits_{1}^{j} V_{j} }} $$
(10)

Table 1 illustrates a significant 12.3% difference between the efficiency of QGA selection method and the Fast Selection method. This difference emphasizes the impact of presence of different influencers in the same network which can cause conflict of information diffusion boundaries.

4.1 Decision-Making Framework

Based on the aforementioned, it is assumed that each nodes could potentially be an influencer, therefore accessing and communication with them is not a serious problem. Therefore, in the results section, the algorithm only shows the best results. But in a more realistic approach in a network like G, some nodes may be not available or might be not willing to spread the information on the network. Therefore, the results of the current optimization may be inadequate for decision makers to choose the best set of influencers. In such circumstances, decision makers can check all network nodes in term of availability before running the algorithm. As checking the availability of all the nodes in a big network can take a long time, it is not recommended especially in crisis situations, Another solution is that decision makers be able to pass on to the next best answer in the case of unavailability of any of influencers in the first best set.

On the other hand, in disaster management, “time” is always a key factor. The relief teams estimation of the volume of different items is mainly time related. Therefore, their schedule to expand awareness of the necessities through the network has some time boundaries. To formulate our problem, it is considered that each node’s diffusion process is reached to its final state and cannot extend more. But it could take several days for a node as an influencer to reach to its final state (see Fig. 3).

Fig. 3.
figure 3

Information diffusion over time

Full size image

Hence, adding the issue of time to the problem and the availability of nodes are also important for the optimal result. It means that best set of influencers may be different from a time boundary to another one, and the best set of influencers in a time boundary may be not available. Therefore, the results should be made available to decision-makers in a way so that they can make better decisions according to different circumstances. In Fig. 4, a chart that helps decision makers make flexible decisions in specific circumstances is proposed, where each circle represents a distinct set of influencers. Decision makers can choose the best set of influencers according to time constraints, and if any of influencers was not available, they will easily pass on to the next best set.

Fig. 4.
figure 4

Decision making framework

Full size image

5 Conclusion

In this paper, the importance of managing people’s awareness of the injured necessities was presented as one of the challenges of disaster management. In the case of inappropriate information diffusion of needs, philanthropists with inappropriate donations, in addition to wasting their donations, might congest the relief chain. Formulating message propagation on social networks in order to create adaptive awareness is the main contribution of this paper. Time constraints in crisis management and influencers’ willingness to collaborate on spreading of the messages, were considered as two important issues to find the best answer, which well answered using a decision making framework.

Determining the actual set of nodes and edges that shapes network structure, till now, is the substantial limitation for this type of research. For further research, the proposed model could be validated in a real disaster context. Also, it is suggested that the impact of the presence of influencers in other social networks and effect of traditional media be considered in formulating this problem.