Abstract
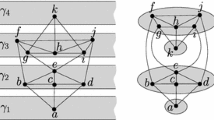
Every planar graph has a concentric representation based on a breadth first search, see [21]. The vertices are placed on concentric circles and the edges are routed as curves without crossings. Here we take the opposite view. A graph with a given partitioning of its vertices onto k concentric circles is k-radial planar, if the edges can be routed monotonic between the circles without crossings. Radial planarity is a generalisation of level planarity, where the vertices are placed on k horizontal lines. We extend the technique for level planarity testing of [18,17,15,16,12,13] and show that radial planarity is decidable in linear time, and that a radial planar embedding can be computed in linear time.
This research has been supported in part by the Deutsche Forschungsgemeinschaft, grant BR 835/9-1.
Chapter PDF
Similar content being viewed by others
References
Bachmaier, C., Brandenburg, F.J., Forster, M.: Radial level planarity testing and embedding in linear time. Technical Report MIP-0303, University of Passau (June 2003)
Bachmaier, C., Raitner, M.: Improved symmetric lists (May 2003) (submitted for publication)
Booth, K.S., Lueker, G.S.: Testing for the consecutive ones property, interval graphs, and graph planarity using PQ-tree algorithms. Journal of Computer and System Sciences 13, 335–379 (1976)
Chiba, N., Nishizeki, T., Abe, S., Ozawa, T.: A linear algorithm for embedding planar graphs using PQ-trees. Journal of Computer and System Sciences 30, 54–76 (1985)
de Fraysseix, H., Pach, J., Pollack, R.: How to draw a planar graph on a grid. Combinatorica 10, 41–51 (1990)
Di Battista, G., Eades, P., Tamassia, R., Tollis, I.G.: Graph drawing: Algorithms for the Visualization of Graphs. Prentice Hall, Englewood Cliffs (1999)
Di Battista, G., Nardelli, E.: Hierarchies and planarity theory. IEEE Transactions on Systems, Man, and Cybernetics 18(6), 1035–1046 (1988)
Di Battista, G., Tamassia, R.: On-line planarity testing. SIAM Journal on Computing 25(5), 956–997 (1996)
Dujmović, V., Fellows, M., Hallett, M., Kitching, M., Liotta, G., McCartin, C., Nishimura, N., Ragde, P., Rosamond, F., Suderman, M., Whitesides, S., Wood, D.R.: On the parameterized complexity of layered graph drawing. In: Meyer auf der Heide, F. (ed.) ESA 2001. LNCS, vol. 2161, pp. 488–499. Springer, Heidelberg (2001)
Even, S.: Algorithms. ch. 7, pp. 148–191. Computer Science Press, Rockville (1979)
GTL. Graph Template Library. University of Passau, http://www.infosun.fmi.uni-passau.de/GTL/
Heath, L.S., Pemmaraju, S.V.: Recognizing leveled-planar dags in linear time. In: Brandenburg, F.J. (ed.) GD 1995. LNCS, vol. 1027, pp. 300–311. Springer, Heidelberg (1996)
Heath, L.S., Pemmaraju, S.V.: Stack and queue layouts of directed acyclic graphs: Part II. SIAM Journal on Computing 28(5), 1588–1626 (1999)
Heath, L.S., Rosenberg, A.L.: Laying out graphs using queues. SIAM Journal on Computing 21(5), 927–958 (1992)
Jünger, M., Leipert, S.: Level planar embedding in linear time. In: Kratochvíl, J. (ed.) GD 1999. LNCS, vol. 1731, pp. 72–81. Springer, Heidelberg (1999)
Jünger, M., Leipert, S.: Level planar embedding in linear time. Journal of Graph Algorithms and Applications 6(1), 67–113 (2002)
Jünger, M., Leipert, S., Mutzel, P.: Level planarity testing in linear time. In: Whitesides, S.H. (ed.) GD 1998. LNCS, vol. 1547, pp. 224–237. Springer, Heidelberg (1999)
Leipert, S.: Level Planarity Testing and Embedding in Linear Time. Dissertation, Mathematisch-Naturwissenschaftliche Fakultät der Universität zu Köln (1998)
Lempel, A., Even, S., Cederbaum, I.: An algorithm for planarity testing of graphs. In: Rosenstiehl, P. (ed.) Theory of Graphs, International Symposium, Rome, July 1966, pp. 215–232. Gordon and Breach, New York (1967)
Sugiyama, K., Tagawa, S., Toda, M.: Methods for visual understanding of hierarchical system structures. IEEE Transactions on Systems, Man, and Cybernetics 11(2), 109–125 (1981)
Ullman, J.D.: Computational Aspects of VLSI. ch. 3.5, pp. 111–114. Computer Science Press, Rockville (1984)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2004 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Bachmaier, C., Brandenburg, F.J., Forster, M. (2004). Radial Level Planarity Testing and Embedding in Linear Time. In: Liotta, G. (eds) Graph Drawing. GD 2003. Lecture Notes in Computer Science, vol 2912. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-24595-7_37
Download citation
DOI: https://doi.org/10.1007/978-3-540-24595-7_37
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-20831-0
Online ISBN: 978-3-540-24595-7
eBook Packages: Springer Book Archive