Abstract
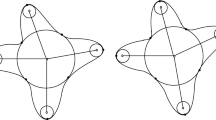
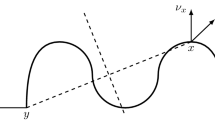
The medial axis in 3D consists of 2D sheets, meeting in 1D curves and special points. In this paper we investigate the consistency conditions which must hold on a collection of sheets meeting in curves and points in order that they could be the medial axis of a smooth surface.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
H.Blum, ‘Biological shape and visual science’, J. Theor. Biol., 38:205–287, 1973.
Bogaevsky, I.A.: Perestroikas of shocks and singularities of minumum functions. Physica D: Nonlinear Phenomena 173, 1–28 (2002)
Chen, S., Parent, R.E.: Shape averaging and its applications to industrial design. CGA 9(1), 47–54 (1989)
Damon, J.: Smoothness and geometry of boundaries associated to skeletal structures II: geometry in the Blum case. To appear in Compositio Mathematica
Damon, J.: Determining the geometry of boundaries of objects from medial data, University of North Carolina at Chapel Hill (2003) (preprint)
Giblin, P.J., Kimia, B.B.: On the intrinsic reconstruction of shape from its symmetries. IEEE Transactions on Pattern Analysis and Machine Intelligence 25, 895–911 (2003)
Giblin, P.J., Kimia, B.B.: A formal classification of 3D medial axis points and their local geometry. IEEE Transactions on Pattern Analysis and Machine Intelligence 26, 238–251 (2004)
Grenander, U., Miller, M.: Computational anatomy: An emerging discipline. Quarterly of Applied Mathematics LVI(4), 617–694 (1998)
Guibas, L., Holleman, R., Kavraki, L.: A probabilistic roadmap planner for flexible objects with a workspace medial axis based sampling approach. In: Proc. Intl. Conf. Intelligent Robots and Systems, Kyongju, Korea, pp. 254–260. IEEE/RSJ (1999)
Holleman, C., Kavraki, L.: A framework for using the workspace medial axis in PRM planners. In: Proceedings of the International Conference on Robotics and Automation, San Fransisco, CA, USA, pp. 1408–1413 (2000)
Leonard, K.: PhD. thesis, Brown University (in preparation)
Leymarie, F.: 3D Shape Representation via Shock Flows. PhD. thesis, Brown University, Providence, RI, USA, . See http://www.lems.brown.edu/leymarie/phd/
Mumford, D.: The Shape of Objects in Two and Three Dimensions. In: Gibbs Lecture (2003), to appear in Notices of the American Mathematical Society
Hallinan, P.L., Gordon, G.G., Yuille, A.L., Giblin, P.J., Mumford, D.: Two- and Three- Dimensional Patterns of the Face. A K Peters, Ltd., Wellesley (1999)
Pelillo, M., Siddiqi, K., Zucker, S.: Matching hierarchical structures using association graphs. IEEE Trans. Pattern Analysis and Machine Intelligence 21(11), 1105–1120 (1999)
Pizer, S.M., Burbeck, C.A.: Object representation by cores: Identifying and representing primitive spatial regions. Vision Research 35(13), 1917–1930 (1995)
Pollitt, A.J.: Euclidean and Affine Symmetry Sets and Medial Axes, Ph.D. thesis, University of Liverpool (in preparation)
Sebastian, T.B., Klein, P.N., Kimia, B.B.: Recognition of shapes by editing shock graphs. In: Proceedings of the Eighth International Conference on Computer Vision, Vancouver, Canada, July 9-12, pp. 755–762. IEEE Computer Society Press, Los Alamitos (2001)
Siddiqi, K., Shokoufandeh, A., Dickinson, S., Zucker, S.: Shock graphs and shape matching. Intl. J. of Computer Vision 35(1), 13–32 (1999)
Siddiqi, K., Tresness, K.J., Kimia, B.B.: Parts of visual form: Ecological and psychophysical aspects. Perception 25, 399–424 (1996)
Siersma, D.: Properties of conflict sets in the plane. In: Janeczko, S., Zakalyukin, V.M. (eds.) Geometry and Topology of Caustics, vol. 50, pp. 267–276. Banach Center Publications, Warsaw (1999)
Sotomayor, J., Siersma, D., Garcia, R.: Curvatures of conflict surfaces in Euclidean 3-space. In: Janeczko, S., Zakalyukin, V.M. (eds.) Geometry and Topology of Caustics, vol. 50, pp. 277–285. Banach Center Publications, Warsaw (1999)
Zhu, S.C., Yuille, A.L.: FORMS: A flexible object recognition and modeling system. Intl. J. of Computer Vision 20(3), 187–212 (1996)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2004 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Pollitt, A., Giblin, P., Kimia, B. (2004). Consistency Conditions on the Medial Axis. In: Pajdla, T., Matas, J. (eds) Computer Vision - ECCV 2004. ECCV 2004. Lecture Notes in Computer Science, vol 3022. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-24671-8_42
Download citation
DOI: https://doi.org/10.1007/978-3-540-24671-8_42
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-21983-5
Online ISBN: 978-3-540-24671-8
eBook Packages: Springer Book Archive