Abstract
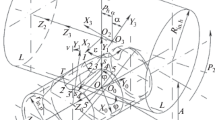
This paper introduces a new method for generating the helical tool-paths for both implicit and parametric surfaces. The basic idea is to describe the helical curves as the solutions of an initial-value problem of ordinary differential equations. This system can be obtained from the fact that the helical curve exhibits a constant angle φ with an arbitrary given vector D, which is assumed to be the axis of the helical curve. The resulting system of differential equations is then integrated by applying standard numerical techniques. The performance of the proposed method is discussed by means of some illustrative examples of helical curves on parametric and implicit surfaces.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Barnhill, R.E. (ed.): Geometry Procesing for Design and Manufacturing. SIAM, Philadelphia (1992)
Beck, J.M., Farouki, R.T., Hinds, J.K.: Surface analysis methods. IEEE Computer Graphics and Applications, 18–36 (December 1986)
Choi, B.K., Jerard, R.B.: Sculptured Surface Machining. Theory and Applications. Kluwer Academic Publishers, Dordrecht (1998)
Farin, G., Hoschek, J., Kim, M.S.: Handbook of Computer Aided Geometric Design. Elsevier Science, Amsterdam (2002)
Hagen, H., Schreiber, T., Gschwind, E.: Methods for surface interrogation. In: Proc. Visualization 1990, pp. 187–193. IEEE Computer Society Press, Los Alamitos (1990)
Hagen, H., Hahman, S., Schreiber, T., Nakajima, Y., Wördenweber, B., Hollemann- Grundstedt, P.: Surface interrogation algorithms. IEEE Computer Graphics and Applications, 53–60 (September 1992)
Hoschek, J., Lasser, D.: Computer-Aided Geometric Design. A.K. Peters, Wellesley (1993)
Klass, R.: Correction of local surface irregularities using reflection lines. CAD 12(2), 73–77 (1980)
Koenderink, J.J., van Doorn, A.J.: Surface shapes and curvature scales. Image and Vision Computing 8(2), 557–565 (1992)
The Mathworks Inc: Using Matlab. Natick, MA (1999)
Patrikalakis, N.M., Maekawa, T.: Shape Interrogation for Computer Aided Design and Manufacturing. Springer, Heidelberg (2002)
Piegl, L., Tiller, W.: The NURBS Book. Springer, Heidelberg (1997)
Poeschl, T.: Detecting surface irregularities using isophotes. CAGD 1(2), 163–168 (1984)
Press, W.H., Teukolsky, S.A., Vetterling, W.T., Flannery, B.P.: Numerical Recipes, 2nd edn. Cambridge University Press, Cambridge (1992)
Struik, D.J.: Lectures on Classical Differential Geometry, 2nd edn. Dover Publications, New York (1988)
Theisel, H., Farin, G.E.: The curvature of characteristic curves on surfaces. IEEE Computer Graphics and Applications, 88–96 (November/December 1997)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2004 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Puig-Pey, J., Gálvez, A., Iglesias, A. (2004). Helical Curves on Surfaces for Computer-Aided Geometric Design and Manufacturing. In: Laganá, A., Gavrilova, M.L., Kumar, V., Mun, Y., Tan, C.J.K., Gervasi, O. (eds) Computational Science and Its Applications – ICCSA 2004. ICCSA 2004. Lecture Notes in Computer Science, vol 3044. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-24709-8_81
Download citation
DOI: https://doi.org/10.1007/978-3-540-24709-8_81
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-22056-5
Online ISBN: 978-3-540-24709-8
eBook Packages: Springer Book Archive