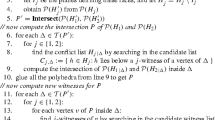Abstract
The similarity of two convex polyhedra A and B may be calculated by evaluating the volume or mixed volume of their Minkowski sum over a specific set of relative orientations. The relative orientations are characterized by the fact that faces and edges of A and B are parallel as much as possible. For one of these relative orientations the similarity measure is optimal. In this article we propose and test a method to reduce the number of relative orientations to be considered by using geometric inequalities in the slope diagrams of A and B. In this way the time complexity of O(n 6) is reduced to O(n 4.5). This is derived, and verified experimentally.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Veltkamp, R.C.: Shape Matching: Similarity Measures and Algorithms. Shape Modeling International, 188–196 (2001)
Heijmans, H.J.A.M., Tuzikov, A.: Similarity and symmetry measures for convex shapes using Minkowski addition. IEEE Trans. Patt. Anal. Mach. Intell. 20(9), 980–993 (1998)
Tuzikov, A.V., Roerdink, J.B.T.M., Heijmans, H.J.A.M.: Similarity measures for convex polyhedra based on Minkowski addition. Pattern Recognition 33(6), 979–995 (2000)
Roerdink, J.B.T.M., Bekker, H.: Similarity measure computation of convex polyhedra revisited. In: Bertrand, G., Imiya, A., Klette, R. (eds.) Digital and Image Geometry. LNCS, vol. 2243, p. 389. Springer, Heidelberg (2002)
Bekker, H., Roerdink, J.B.T.M.: Calculating critical orientations of polyhedra for similarity measure evaluation. In: Proc. 2nd Annual IASTED International Conference on Computer Graphics and Imaging, Palm Springs, California USA, October 25-27, pp. 106–111 (1999)
Sangwine-Yager, J.R.: Mixed volumes. Handbook of convex geometry, vol. 1.2. Elsevier science publishers B.V., Amsterdam (1993)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2004 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Bekker, H., Brink, A. (2004). Reducing the Time Complexity of Minkowski-Sum Based Similarity Calculations by Using Geometric Inequalities. In: Laganá, A., Gavrilova, M.L., Kumar, V., Mun, Y., Tan, C.J.K., Gervasi, O. (eds) Computational Science and Its Applications – ICCSA 2004. ICCSA 2004. Lecture Notes in Computer Science, vol 3045. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-24767-8_4
Download citation
DOI: https://doi.org/10.1007/978-3-540-24767-8_4
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-22057-2
Online ISBN: 978-3-540-24767-8
eBook Packages: Springer Book Archive