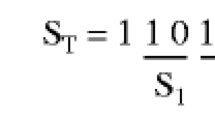Skip to main content
Springer Nature Link
Log in

Generation of Unordered Binary Trees

  • Conference paper
Computational Science and Its Applications – ICCSA 2004 (ICCSA 2004)

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 3045))

Included in the following conference series:

  • 1203 Accesses

Abstract

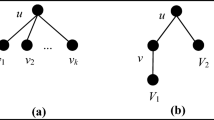
A binary unordered tree is a tree where each internal node has two children and the relative order of the subtrees of a node is not important (i.e. two trees are different if they differ only in the respective ordering of subtrees of nodes). We present a new method to generate all binary rooted unordered trees with n internal nodes, without duplications, in O(log n) time.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Beyer, T., Hedetniemi, M.: Constant Time Generation of Rooted Trees. SIAM Journal on Computing 9, 706–712 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  2. Kozina, A.V.: Coding and Generation of NonisomorphicTrees. Cybernetics 25, 645–651 (1979)

    Google Scholar 

  3. Kubicka, E., Kubicki, G.: Constant Time Algorithm for Generating Binary Rooted Trees. Congressus Numerantium 90, 57–64 (1992)

    MathSciNet  Google Scholar 

  4. Li, G., Ruskey, F.: The Advantages of Forward Thinking in Generating Rooted and Free Trees. Extended Abstract SODA (1999)

    Google Scholar 

  5. McKay, B.D.: Isomorph-Free Exhaustive Generation. Journal of Algorithms 26, 306–324 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  6. Murtagh, F.: Counting dendrograms: a survey. DiscreteApplied Mathematics 7, 191–199 (1984)

    Article  MATH  MathSciNet  Google Scholar 

  7. Pallo, J.M.: Enumerating, Ranking and Unranking Binary Trees. The Computer Journal 29, 171–175 (1986)

    Article  MATH  MathSciNet  Google Scholar 

  8. Pallo, J.M.: Lexicographic Generation of Binary Unordered Trees. Pattern Recognition Letters 10, 217–221 (1989)

    Article  MATH  Google Scholar 

  9. Wright, R.A., Richmond, B., Odlyzko, A., McKay, B.D.: Constant Time Generation of Free Trees. SIAM Journal on Computing 15, 540–548 (1986)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Istituto di Informatica e Telematica, CNR, Area della Ricerca, Via Moruzzi 1, 56124, PISA, ITALY

    Brice Effantin

Authors
  1. Brice Effantin
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Department of Chemistry, University of Perugia, Via Elce di Sotto, 8, I-06123, Perugia, Italy

    Antonio Laganá

  2. Department of Computer Science, University of Calgary, 2500 University Drive N.W., T2N 1N4, Calgary, AB, Canada

    Marina L. Gavrilova

  3. William Norris Professor, Head of the Computer Science and Engineering Department, University of Minnesota, USA

    Vipin Kumar

  4. School of Computing, Soongsil University, Seoul, Korea

    Youngsong Mun

  5. OptimaNumerics Ltd., Cathedral House, 23-31 Waring Street, BT1 2DX, Belfast, UK

    C. J. Kenneth Tan

  6. Department of Mathematics and Computer Science, University of Perugia, via Vanvitelli, 1, I-06123, Perugia, Italy

    Osvaldo Gervasi

Rights and permissions

Reprints and permissions

Copyright information

© 2004 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Effantin, B. (2004). Generation of Unordered Binary Trees. In: Laganá, A., Gavrilova, M.L., Kumar, V., Mun, Y., Tan, C.J.K., Gervasi, O. (eds) Computational Science and Its Applications – ICCSA 2004. ICCSA 2004. Lecture Notes in Computer Science, vol 3045. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-24767-8_68

Download citation

  • DOI: https://doi.org/10.1007/978-3-540-24767-8_68

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-540-22057-2

  • Online ISBN: 978-3-540-24767-8

  • eBook Packages: Springer Book Archive

Publish with us

Policies and ethics