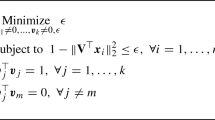Abstract
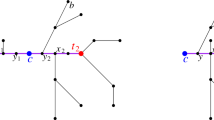
We consider the problem of fitting metric data on n points to a path (line) metric. Our objective is to minimize the total additive distortion of this mapping. The total additive distortion is the sum of errors in all pairwise distances in the input data. This problem has been shown to be NP-hard by [13]. We give an O(logn) approximation for this problem by using Garg et al.’s [10] algorithm for the multi-cut problem as a subroutine. Our algorithm also gives an O(log1/p n) approximation for the L p norm of the additive distortion.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Agarwala, R., Bafna, V., Farach, M., Narayanan, B.O., Paterson, M., Thorup, M.: On the approximability of numerical taxonomy (fitting distances by tree metrics). In: Symposium on Discrete Algorithms, pp. 365–372 (1996)
Badoiu, M., Indyk, P., Rabinovich, Y.: Approximate algorithms for embedding metrics into low-dimensional spaces. (2003) (Unpublished manuscript)
Barthélemy, J.-P., Guénoche, A.: Trees and proximity representations. Wiley, New York (1991)
Blum, A., Chawla, S., Karger, D., Meyerson, A., Minkoff, M., Lane, T.: Approximation algorithms for orienteering and discounted-reward tsp. In: IEEE Symposium on Foundations of Computer Science (2003)
Cavalli-Sforza, L., Edwards, A.: Phylogenetic analysis models and estimation procedures. American Journal of Human Genetics 19, 233–257 (1967)
Deza, M., Laurent, M.: Geometry of Cuts and Metrics. Springer, Berlin (1997)
Dhamdhere, K., Gupta, A., Ravi, R.: Approximating average distortion for embeddings into line. In: Symposium on Theoretical Aspects of Computer Science, STACS (2004)
Farach, M., Kannan, S., Warnow, T.: A robust model for finding optimal evolutionary trees. Algorithmica 13, 155–179 (1995)
Garey, M.R., Johnson, D.S.: Computers and Intractability: A Guide to the Theory of NP-completeness. W. H. Freeman, San Fransisco (1979)
Garg, N., Vazirani, V., Yannakakis, M.: Approximate max-flow min-(multi)cut theorems and their applications. SIAM Journal on Computing 25(2), 235–251 (1996)
Håstad, J., Ivansson, L., Lagergren, J.: Fitting points on the real line and its application to RH mapping. In: European Symposium on Algorithms, pp. 465–476 (1998)
Klein, P., Agarwal, A., Ravi, R., Rao, S.: Approximation through multicommodity flow. In: IEEE Symposium on Foundations of Computer Science, pp. 726–737 (1990)
Saxe, J.B.: Embeddability of graphs into k-space is strongly np-hard. In: Allerton Conference in Communication, Control and Computing, pp. 480–489 (1979)
Sneath, P.H.A., Sokal, R.R.: Numerical Taxonomy. W. H. Freeman, San Fransisco (1973)
Waterman, M.S., Smith, T.S., Singh, M., Beyer, W.A.: Additive evolutionary trees. Journal of Theoretical Biology 64, 199–213 (1977)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2004 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Dhamdhere, K. (2004). Approximating Additive Distortion of Embeddings into Line Metrics. In: Jansen, K., Khanna, S., Rolim, J.D.P., Ron, D. (eds) Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques. RANDOM APPROX 2004 2004. Lecture Notes in Computer Science, vol 3122. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-27821-4_9
Download citation
DOI: https://doi.org/10.1007/978-3-540-27821-4_9
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-22894-3
Online ISBN: 978-3-540-27821-4
eBook Packages: Springer Book Archive