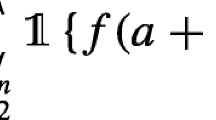Abstract
We study the random composition of a small family of O(n 3) simple permutations on {0,1}n. Specifically we ask what is the number of compositions needed to achieve a permutation that is close to k-wise independent. We improve on a result of Gowers [8] and show that up to a polylogarithmic factor, n 3 k 3 compositions of random permutations from this family suffice. We further show that the result applies to the stronger notion of k-wise independence against adaptive adversaries. This question is essentially about the rapid mixing of the random walk on a certain graph, and we approach it using a new technique to construct canonical paths. We also show that if we are willing to use a much larger family of simple permutations then we can guaranty closeness to k-wise independence with fewer compositions and fewer random bits.
This is a preview of subscription content, log in via an institution to check access.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Aldous, D., Fill, J.A.: Reversible markov chains and random walks on graphs, http://stat-www.berkeley.edu/users/aldous/RWG/book.html
Barenco, A., Bennett, C.H., Cleve, R., DiVincenzo, D.P., Margolus, N., Shor, P., Sleator, T., Smolin, J.A., Weinfurter, H.: Elementary gates for quantum computation. Phys. Rev. A 52(5), 3457–3467 (1995)
Cameron, P.J.: Permutation groups. London Mathematical Society Student Texts, vol. 45. Cambridge University Press, Cambridge (1999)
Chung, F.R.K., Graham, R.L.: Stratified random walks on the n-cube. Random Structures Algorithms 11(3), 199–222 (1997)
Cleve, R.: Complexity theoretic issues concerning block ciphers related to D.E.S. In: Menezes, A., Vanstone, S.A. (eds.) CRYPTO 1990. LNCS, vol. 537, pp. 530–544. Springer, Heidelberg (1991)
Coppersmith, D., Grossman, E.: Generators for certain alternating groups with applications to cryptography. SIAM J. Appl. Math. 29(4), 624–627 (1975)
Dixon, J.D., Mortimer, B.: Permutation groups. Graduate Texts in Mathematics, vol. 163. Springer, New York (1996)
Gowers, W.T.: An almost m-wise independent random permutation of the cube. Combin. Probab. Comput. 5(2), 119–130 (1996)
Jerrum, M.: Counting, sampling and integrating: algorithms and complexity. Lectures in Mathematics ETH Zürich. Birkhäuser, Basel (2003)
Maurer, U., Pietrzak, K.: Composition of random systems: When two weak make one strong. In: The First Theory of Cryptography Conference (2004)
Sinclair, A., Jerrum, M.: Approximate counting, uniform generation and rapidly mixing Markov chains. Inform. and Comput. 82(1), 93–133 (1989)
Vaudenay, S.: Adaptive-attack norm for decorrelation and super-pseudorandomness. In: Heys, H.M., Adams, C.M. (eds.) SAC 1999. LNCS, vol. 1758, pp. 49–61. Springer, Heidelberg (2000)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2004 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Hoory, S., Magen, A., Myers, S., Rackoff, C. (2004). Simple Permutations Mix Well. In: Díaz, J., Karhumäki, J., Lepistö, A., Sannella, D. (eds) Automata, Languages and Programming. ICALP 2004. Lecture Notes in Computer Science, vol 3142. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-27836-8_65
Download citation
DOI: https://doi.org/10.1007/978-3-540-27836-8_65
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-22849-3
Online ISBN: 978-3-540-27836-8
eBook Packages: Springer Book Archive