Abstract
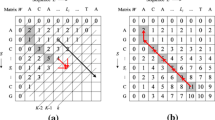
The length of the longest common subsequence (LCS) between two strings of M and N characters can be computed by O(M × N) dynamic programming algorithms that can execute in O(M+N) on a linear systolic array. If the strings are run-length encoded, LCS can be computed by an O(mN+Mn–mn) algorithm, called RLE-LCS, where m and n are the numbers of runs of the two strings.
In this paper we propose a modified RLE-LCS algorithm mappable on a linear systolic array.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
Smith, T.F., Waterman, M.S.: Identification of common molecular subsequences. Journal of Molecular Biology 48, 195–197 (1981)
Lopresti, D.: P-NAC: A Systolic Array for Comparing Nucleic Acid Sequences. Computer 24(11), 6–13 (1987)
Sayoood, K., Fow, E. (eds.): Introduction to Data Compression, 2nd edn. Morgan Kaufmann, San Francisco (2000)
Freschi, V., Bogliolo, A.: Longest Common Subsequence between Run-Length-Encoded Strings: a New Algorithm with Improved Parallelism. Information Processing Letters 90, 167–173 (2004)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2004 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Bogliolo, A., Freschi, V., Miglioli, F., Canella, M. (2004). FPGA-Based Parallel Comparison of Run-Length-Encoded Strings. In: Becker, J., Platzner, M., Vernalde, S. (eds) Field Programmable Logic and Application. FPL 2004. Lecture Notes in Computer Science, vol 3203. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-30117-2_137
Download citation
DOI: https://doi.org/10.1007/978-3-540-30117-2_137
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-22989-6
Online ISBN: 978-3-540-30117-2
eBook Packages: Springer Book Archive