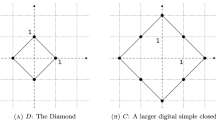
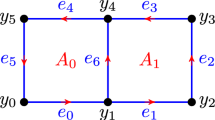
Abstract
Many combinatorial structures have been designed to represent the topology of space subdivisions and images. We focus here on two particular models, namely the n-G-maps used in geometric modeling and computational geometry and the n-surfaces used in discrete imagery. We show that a subclass of n-G-maps is equivalent to n-surfaces. We exhibit a local property characterising this subclass, which is easy to check algorithmatically. Finally, the proofs being constructive, we show how to switch from one representation to another effectively.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Alayrangues, S., Lachaud, J.-O.: Equivalence Between Order and Cell Complex Representations. In: Proc. Computer Vision Winter Workshop, CVWW 2002 (2002)
Alayrangues, S., Daragon, X., Lachaud, J.-O., Lienhardt, P.: Equivalence between Regular n-G-maps and n-surfaces, Research Report, http://www.labri.fr/Labri/Publications/Publis-fr.htm
Bertrand, G.: New Notions for Discrete Geometry. In: Bertrand, G., Couprie, M., Perroton, L. (eds.) DGCI 1999. LNCS, vol. 1568, p. 218. Springer, Heidelberg (1999)
Bertrand, G.: A Model for Digital Topology. In: Bertrand, G., Couprie, M., Perroton, L. (eds.) DGCI 1999. LNCS, vol. 1568, p. 229. Springer, Heidelberg (1999)
Björner, A.: Topological methods. In: Handbook of combinatorics, vol. 2. MIT Press, Cambridge (1995)
Brisson, E.: Representing Geometric Structures in d Dimensions: Topology and Order. In: Proceedings of the Fifth Annual Symposium on Computational Geometry (1989)
Brun, L., Kropatsch, W.: Contraction Kernels and Combinatorial Maps. In: 3rd IAPR-TC15 Workshop on Graph-based Representations in Pattern Recognition (2001)
Daragon, X., Couprie, M., Bertrand, G.: New “marching-cubes-like” algorithm for Alexandroff-Khalimsky spaces. In: Proc. of SPIE: Vision Geometry, vol. XI (2002)
Daragon, X., Couprie, M., Bertrand, G.: Discrete Frontiers. In: Nyström, I., Sanniti di Baja, G., Svensson, S. (eds.) DGCI 2003. LNCS, vol. 2886, pp. 236–245. Springer, Heidelberg (2003)
Edelsbrunner, H.: Algorithms in combinatorial geometry. Springer-Verlag New York, Inc. (1987)
Elter, H.: Etude de structures combinatoires pour la representation de complexes cellulaires, Universit Louis Pasteur, Strasbourg, France (1994)
Evako, A.V., Kopperman, R., Mukhin, Y.V.: Dimensional properties of graphs and digital spaces. Journal of Mathematical Imaging and Vision (1996)
Hatcher, A.: Algebraic Topology. Cambridge University Press, Cambridge (2002)
Lienhardt, P.: Subdivisions of n-dimensional spaces and n-dimensional generalized maps. In: Proc. 5th Annual ACM Symp. on Computational Geometry (1989)
Lienhardt, P.: Topological models for boundary representation: a comparison with n-dimensional generalized maps. Computer-Aided Design (1991)
Lienhardt, P.: N-dimensional generalized combinatorial maps and cellular quasi-manifolds. International Journal of Computational Geometry and Applications (1994)
May, P.: Simplicial objects in algebraic topology, von Nostrand (1967)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2004 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Alayrangues, S., Daragon, X., Lachaud, JO., Lienhardt, P. (2004). Equivalence Between Regular n-G-Maps and n-Surfaces. In: Klette, R., Žunić, J. (eds) Combinatorial Image Analysis. IWCIA 2004. Lecture Notes in Computer Science, vol 3322. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-30503-3_10
Download citation
DOI: https://doi.org/10.1007/978-3-540-30503-3_10
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-23942-0
Online ISBN: 978-3-540-30503-3
eBook Packages: Computer ScienceComputer Science (R0)