Abstract
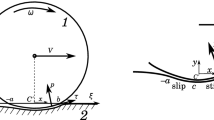
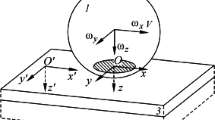
In this paper a steady-state rolling problem with nonlinear friction, for rigid-plastic, rate sensitive and slightly compressible materials is considered. Its variational formulation is given and existence and uniqueness results, obtained with the help of successive iteration methods are presented. Considering the slight material compressibility as a method of penalisation, it is further shown, that when the compressibility parameter tends to zero the solution of the rolling problem for incompressible materials is approached.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Zienkiewicz, O.C.: Flow formulation for numerical solution of forming processes. In: Pittman, J.F.T., Zienkiewicz, O.C., Wood, R.D., Alexander, J.M. (eds.) Numerical Analysis of Forming Processes, pp. 1–44. John Wiley & Sons, Chichester (1984)
Kobayashi, S., Oh, S.-I., Altan, T.: Metal Forming and the Finite Element Method. Oxford University Press, Oxford (1989)
Mori, K.-I.: Rigid-plastic finite element solution of forming processes. In: Pietrzyk, M., Kusiak, J., Sadok, L., Engel, Z. (eds.) Huber’s Yield Criterion in Plasticity, pp. 73–99. AGH, Krakow (1994)
Angelov, T., Baltov, A., Nedev, A.: Existence and uniqueness of the solution of a rigid-plastic rolling problem. Int. J. Engng. Sci. 33, 1251–1261 (1995)
Angelov, T.: A secant modulus method for a rigid-plastic rolling problem. Int. J. Nonl. Mech. 30, 169–178 (1995)
Angelov, T., Liolios, A.: Variational and numerical approach to a steady-state rolling problem (submitted)
Duvaut, G., Lions, J.-L.: Les Inequations en Mechanique en Physique. Dunod, Paris (1972)
Kikuchi, N., Oden, J.T.: Contact Problems in Elasticity: A Study of Variational Inequalities and Finite Element Methods. SIAM, Philadelphia (1988)
Glowinski, R., Lions, J.-L., Tremolieres, R.: Numerical Analysis of Variational Inequalities. North-Holland, Amsterdam (1981)
Glowinski, R.: Numerical Methods for Nonlinear Variational Problems. Springer, Berlin (1984)
Mikhlin, S.G.: The Numerical Performance of Variational Methods. Walters-Noordhoff, The Netherlands (1971)
Nečas, J., Hlavaček, I.: Mathematical Theory of Elastic and Elasto-Plastic Bodies: An Introduction. Elsevier, Amsterdam (1981)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2005 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Angelov, T.A. (2005). On the Solvability of the Steady-State Rolling Problem. In: Li, Z., Vulkov, L., Waśniewski, J. (eds) Numerical Analysis and Its Applications. NAA 2004. Lecture Notes in Computer Science, vol 3401. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-31852-1_13
Download citation
DOI: https://doi.org/10.1007/978-3-540-31852-1_13
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-24937-5
Online ISBN: 978-3-540-31852-1
eBook Packages: Computer ScienceComputer Science (R0)