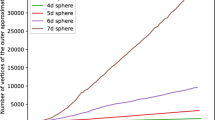
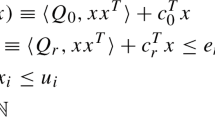Abstract
In recent years, interval constraint-based solvers have shown their ability to efficiently solve complex instances of non-linear numerical CSPs. However, most of the working systems are designed to deliver point-wise solutions with an arbitrary accuracy. This works generally well for systems with isolated solutions but less well when there is a continuum of feasible points (e.g. under-constrained problems, problems with inequalities). In many practical applications, such large sets of solutions express equally relevant alternatives which need to be identified as completely as possible. In this paper, we address the issue of constructing concise inner and outer approximations of the complete solution set for non-linear CSPs. We propose a technique which combines the extreme vertex representation of orthogonal polyhedra 1,2,3, as defined in computational geometry, with adapted splitting strategies 4 to construct the approximations as unions of interval boxes. This allows for compacting the explicit representation of the complete solution set and improves efficiency.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Aguilera, A.: Orthogonal Polyhedra: Study and Application. PhD thesis, Universitat Politècnica de Catalunya, Barcelona, Spain (1998)
Bournez, O., Maler, O., Pnueli, A.: Orthogonal Polyhedra: Representation and Computation. In: Vaandrager, F.W., van Schuppen, J.H. (eds.) HSCC 1999. LNCS, vol. 1569, pp. 46–60. Springer, Heidelberg (1999)
Bournez, O., Maler, O.: On the Representation of Timed Polyhedra. In: Welzl, E., Montanari, U., Rolim, J.D.P. (eds.) ICALP 2000. LNCS, vol. 1853, p. 793. Springer, Heidelberg (2000)
Silaghi, M.C., Sam-Haroud, D., Faltings, B.: Search Techniques for Non-linear CSPs with Inequalities. In: Proceedings of the 14th Canadian Conference on AI (2001)
Van Hentenryck, P.: A Gentle Introduction to Numerica (1998)
ILOG: ILOG Solver. Reference Manual (2002)
Jaulin, L.: Solution Globale et Guarantie de Problèmes Ensemblistes: Application à l’Estimation Non Linéaire et à la Commande Robuste. PhD thesis, Université Paris-Sud, Orsay (1994)
Sam-Haroud, D., Faltings, B.: Consistency Techniques for Continuous Constraints. Constraints 1(1-2), 85–118 (1996)
Garloff, J., Graf, B.: Solving Strict Polynomial Inequalities by Bernstein Expansion. In: Symbolic Methods in Control System Analysis and Design, pp. 339–352 (1999)
Benhamou, F., Goualard, F.: Universally Quantified Interval Constraints. In: Dechter, R. (ed.) CP 2000. LNCS, vol. 1894, pp. 67–82. Springer, Heidelberg (2000)
Vu, X.H., Sam-Haroud, D., Silaghi, M.C.: Approximation Techniques for Nonlinear Problems with Continuum of Solutions. In: Koenig, S., Holte, R.C. (eds.) SARA 2002. LNCS (LNAI), vol. 2371, pp. 224–241. Springer, Heidelberg (2002)
Lhomme, O.: Consistency Techniques for Numeric CSPs. In: Proceedings of IJCAI 1993 (1993)
Collavizza, H., Delobel, F., Rueher, M.: Extending Consistent Domains of Numeric CSP. In: Proceedings of IJCAI 1999 (1999)
Van Iwaarden, R.J.: An Improved Unconstrainted Global Optimization Algorithm. PhD thesis, University of Colorado at Denver, USA (1996)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2003 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Vu, XH., Sam-Haroud, D., Silaghi, MC. (2003). Numerical Constraint Satisfaction Problems with Non-isolated Solutions. In: Bliek, C., Jermann, C., Neumaier, A. (eds) Global Optimization and Constraint Satisfaction. COCOS 2002. Lecture Notes in Computer Science, vol 2861. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-39901-8_15
Download citation
DOI: https://doi.org/10.1007/978-3-540-39901-8_15
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-20463-3
Online ISBN: 978-3-540-39901-8
eBook Packages: Springer Book Archive