Abstract
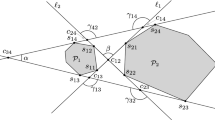
We investigate equitable 3-cuttings of two mass distributions in the plane (partitions of the plane into 3 sectors with a common apex such that each sector contains 1/3 of each mass). We prove the existence of a continuum of equitable 3-cuttings that satisfy some closure property. This permits us to generalize earlier results on both convex and non-convex equitable 3-cuttings with additional constraints.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Bárány, I.: Geometric and combinatorial applications of Borsuk’s theorem. In: Pach, J. (ed.) New Trends in Discrete and Computational Geometry. Algorithms and Combinatorics, vol. 10, pp. 235–249. Springer, Heidelberg (1993)
Bárány, I., Matoušek, J.: Simultaneous partitions of measures by k-fans. Discrete Comput. Geom. 25(3), 317–334 (2001)
Bárány, I., Matoušek, J.: Equipartition of two measures by a 4-fan. Discrete Comput. Geom. 27(3), 293–301 (2002)
Bespamyatnikh, S., Kirkpatrick, D., Snoeyink, J.: Generalizing ham sandwich cuts to equitable subdivisions. Discrete Comput. Geom. 24(4), 605–622 (2000)
Díaz, M., O’Rourke, J.: Ham-sandwich sectioning of polygons. In: Proc. 2nd Canad. Conf. Comput. Geom., pp. 282–286 (1990)
Dobkin, D.P., Edelsbrunner, H.: Ham-sandwich theorems applied to intersection problems. In: Proc. 10th Internat. Workshop Graph-Theoret. Concepts Comput. Sci., pp. 88–99 (1984)
Edelsbrunner, H., Waupotitsch, R.: Computing a ham-sandwich cut in two dimensions. J. Symbolic Comput. 2, 171–178 (1986)
Ito, H., Uehara, H., Yokoyama, M.: 2-dimension ham sandwich theorem for partitioning into three convex pieces. In: Akiyama, J., Kano, M., Urabe, M. (eds.) JCDCG 1998. LNCS, vol. 1763, pp. 129–157. Springer, Heidelberg (2000)
Kaneko, A., Kano, M.: Balanced partitions of two sets of points in the plane. Comput. Geom. Theory Appl. 13, 253–261 (1999)
Lo, C.-Y., Matoušek, J., Steiger, W.: Ham-sandwich cuts in \(\Re^{d}\). In: Proc. 24th Annu. ACM Sympos. Theory Comput., pp. 539–545 (1992)
Lo, C.-Y., Matoušek, J., Steiger, W.L.: Algorithms for ham-sandwich cuts. Discrete Comput. Geom. 11, 433–452 (1994)
Lo, C.-Y., Steiger, W.: An optimal-time algorithm for ham-sandwich cuts in the plane. In: Proc. 2nd Canad. Conf. Comput. Geom., pp. 5–9 (1990)
Sakai, T.: Balanced convex partitions of measures in ℝ2. Graphs and Combinatorics 18(1), 169–192 (2002)
Steiger, W.: Algorithms for ham sandwich cuts. In: Proc. 5th Canad. Conf. Comput. Geom., p. 48 (1993)
Vrećica, S.T., Živaljević, R.T.: Conical equipartitions of mass distributions. Discrete Comput. Geom. 25(3), 335–350 (2001)
Živaljević, R.T.: Topological methods. In: Goodman, J.E., O’Rourke, J. (eds.) Handbook of Discrete and Computational Geometry, ch. 11, pp. 209–224. CRC Press LLC, Boca Raton (1997)
Živaljević, R.T., Vrećica, S.T.: An extension of the ham sandwich theorem. Bull. London Math. Soc. 22, 183–186 (1990)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2003 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Bespamyatnikh, S., Kirkpatrick, D. (2003). Constrained Equitable 3-Cuttings. In: Akiyama, J., Kano, M. (eds) Discrete and Computational Geometry. JCDCG 2002. Lecture Notes in Computer Science, vol 2866. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-44400-8_8
Download citation
DOI: https://doi.org/10.1007/978-3-540-44400-8_8
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-20776-4
Online ISBN: 978-3-540-44400-8
eBook Packages: Springer Book Archive