Angle Optimization in Target Tracking

Abstract

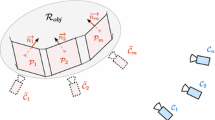
We consider the problem of tracking n targets in the plane using 2n cameras, where tracking each target requires two distinct cameras. A single camera (modeled as a point) sees a target point in a certain direction, ideally with unlimited precision, and thus two cameras (not collinear with the target) unambiguously determine the position of the target. In reality, due to the imprecision of the cameras, instead of a single viewing direction a target defines only a viewing cone, and so two cameras localize a target only within the intersection of two such cones. In general, the true localization error is a complicated function of the angle subtended by the two cameras at the target (the tracking angle), but a commonly accepted tenet is that an angle of 90° is close to the ideal. In this paper, we consider several algorithmic problems related to this so-called “focus of attention” problem. In particular, we show that the problem of deciding whether each of n given targets can be tracked with 90° is NP-complete. For the special case where the cameras are placed along a single line while the targets are located anywhere in the plane, we show a 2-approximation both for the sum of tracking angles and the bottleneck tracking angle (i.e., the smallest tracking angle) maximization problems (which is a natural goal whenever targets and cameras are far from each other). Lastly, for the uniform placement of cameras along the line, we further improve the result to a PTAS.