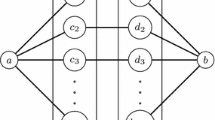
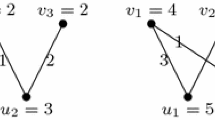
Abstract
We study the complexity of combinatorial problems that consist of competing infeasibility and optimization components. In particular, we investigate the complexity of the connection subgraph problem, which occurs, e.g., in resource environment economics and social networks. We present results on its worst-case hardness and approximability. We then provide a typical-case analysis by means of a detailed computational study. First, we identify an easy-hard-easy pattern, coinciding with the feasibility phase transition of the problem. Second, our experimental results reveal an interesting interplay between feasibility and optimization. They surprisingly show that proving optimality of the solution of the feasible instances can be substantially easier than proving infeasibility of the infeasible instances in a computationally hard region of the problem space. We also observe an intriguing easy-hard-easy profile for the optimization component itself.
Research supported by the Intelligent Information Systems Institute (IISI), Cornell University (AFOSR grant F49620-01-1-0076).
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Ando, A., Camm, J., Polasky, S., Solow, A.: Special distributions, land values, and efficient conservation. Science 279(5359), 2126–2128 (1998)
Bern, M.W., Plassmann, P.E.: The Steiner tree problem with edge lengths 1 and 2. Information Processing Letters 32(4), 171–176 (1989)
Camm, J.D., Norman, S.K., Polasky, S., Solow, A.R.: Nature reserve site selection to maximize expected species covered. Operations Research 50(6), 946–955 (2002)
Dinur, I., Safra, S.: On the hardness of approximating minimum vertex cover. Annals of Mathematics 162(1), 439–486 (2005)
Faloutsos, C., McCurley, K.S., Tomkins, A.: Fast discovery of connection subgraphs. In: Proceedings of the 2004 ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 118–127. ACM Press, New York (2004)
Gent, I.P., Walsh, T.: The TSP Phase Transition. Artificial Intelligence 88(1–2), 349–358 (1996)
ILOG, SA. CPLEX 10.1 Reference Manual (2006)
Prömel, H.J., Steger, A.: The Steiner Tree Problem: A Tour Through Graphs, Algorithms, and Complexity. Vieweg, Wiesbaden (2002)
Simberloff, D., Farr, J.A., Cox, J., Mehlman, D.W.: Movement corridors: Conservation bargains or poor invesments? Conservation Biology 6, 493–504 (1997)
Zhang, W., Korf, R.E.: A Study of Complexity Transitions on the Asymmetric Traveling Salesman Problem. Artificial Intelligence 81, 223–239 (1996)
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 2007 Springer Berlin Heidelberg
About this paper
Cite this paper
Conrad, J., Gomes, C.P., van Hoeve, WJ., Sabharwal, A., Suter, J. (2007). Connections in Networks: Hardness of Feasibility Versus Optimality. In: Van Hentenryck, P., Wolsey, L. (eds) Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems. CPAIOR 2007. Lecture Notes in Computer Science, vol 4510. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-72397-4_2
Download citation
DOI: https://doi.org/10.1007/978-3-540-72397-4_2
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-72396-7
Online ISBN: 978-3-540-72397-4
eBook Packages: Computer ScienceComputer Science (R0)