Worst-Case Evaluation of Flexible Solutions in Disjunctive Scheduling Problems

Abstract

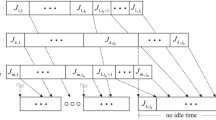
In this paper, we consider the problem of evaluating the worst case performance of flexible solutions in non-preemptive disjunctive scheduling. A flexible solution represents a set of semi-active schedules and is characterized by a partial order on each machine. A flexible solution can be used on-line to absorb the impact of some data disturbances related for example to job arrival, tool availability and machine breakdowns. Providing a flexible solution is useful in practice only if it can be assorted with an evaluation of the complete schedules that can be obtained by extension. For this purpose, we suggest to use only the best case and the worst case performance. The best case performance is an ideal performance that can be achieved only if the on-line conditions allow to implement the best schedule among the set of schedules characterized by the flexible solution. In contrast, the worst case performance indicates how poorly the flexible solution may perform. These performances can be obtained by solving corresponding minimization and maximization problems. We focus here on maximization problems when a regular minmax objective function is considered. In this case, the worse objective function value can be determined by computing the worse completion time of each operation separately. We show that this problem can be solved by finding an elementary longest path in the disjunctive graph representing the problem with additional constraints. In the special case of the flow-shop problem with release dates and additional precedence constraints, we give a polynomial algorithm that determines the worst case performance of a flexible solution.