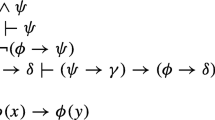Abstract
This paper considers logical formulas built on the single binary connector of implication and a finite number of variables. When the number of variables becomes large, we prove the following quantitative results: asymptotically, all classical tautologies are simple tautologies. It follows that asymptotically, all classical tautologies are intuitionistic.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Chauvin, B., Flajolet, P., Gardy, D., Gittenberger, B.: And/Or trees revisited. Combinatorics, Probability and Computing 13(4-5), 475–497 (2004)
Flajolet, P., Sedgewick, R.: Analytic combinatorics: functional equations, rational and algebraic functions, INRIA, Number 4103 (2001)
Flajolet, P., Sedgewick, R.: Analytic combinatorics. Book in preparation (2007), available at http://algo.inria.fr/flajolet/Publications/books.html
Gardy, D.: Random Boolean expressions, Colloquium on Computational Logic and Applications. In: Proceedings in DMTCS, Chambery (France), June 2005, pp. 1–36 (2006)
Gardy, D., Woods, A.: And/or tree probabilities of Boolean function. Discrete Mathematics and Theoretical Computer Science, 139–146 (2005)
Kostrzycka, Z., Zaionc, M.: Statistics of intuitionnistic versus classical logic. Studia Logica 76(3), 307–328 (2004)
Lefmann, H., Savický, P.: Some typical properties of large And/Or Boolean formulas. Random Structures and Algorithms 10, 337–351 (1997)
Matecki, G.: Asymptotic density for equivalence. Electronic Notes in Theoretical Computer Science 140, 81–91 (2005)
Moczurad, M., Tyszkiewicz, J., Zaionc, M.: Statistical properties of simple types. Mathematical Structures in Computer Science 10(5), 575–594 (2000)
Sørensen, M., Urzyczyn, P.: Lectures on the Curry-Howard Isomorphism. Studies in Logic and the Foundations of Mathematics 149 (2006)
Wilf, H.: Generatingfunctionology, 2nd edn. Academic Press, Boston (1994)
Zaionc, M.: On the asymptotic density of tautologies in logic of implication and negation. Reports on Mathematical Logic 39, 67–87 (2005)
Zaionc, M.: Probability distribution for simple tautologies. Theoretical Computer Science 355(2), 243–260 (2006)
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 2007 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Fournier, H., Gardy, D., Genitrini, A., Zaionc, M. (2007). Classical and Intuitionistic Logic Are Asymptotically Identical. In: Duparc, J., Henzinger, T.A. (eds) Computer Science Logic. CSL 2007. Lecture Notes in Computer Science, vol 4646. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-74915-8_16
Download citation
DOI: https://doi.org/10.1007/978-3-540-74915-8_16
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-74914-1
Online ISBN: 978-3-540-74915-8
eBook Packages: Computer ScienceComputer Science (R0)