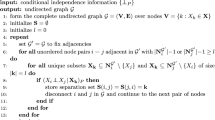Abstract
In the score plus search based Bayesian networks structure learning approach, the most used method is hill climbing (HC), because its implementation is good trade-off between CPU requirements, accuracy of the obtained model, and ease of implementation. Because of these features and to the fact that HC with the classical operators guarantees to obtain a minimal I-map, this approach is really appropriate to deal with high dimensional domains. In this paper we revisited a previously developed HC algorithm (termed constrained HC, or CHC in short) that takes advantage of some scoring metrics properties in order to restrict during the search the parent set of each node. The main drawback of CHC is that there is no warranty of obtaining a minimal I-map, and so the algorithm includes a second stage in which an unconstrained HC is launched by taking as initial solution the one returned by the constrained search stage. In this paper we modify CHC in order to guarantee that its output is a minimal I-map and so the second stage is not needed. In this way we save a considerable amount of CPU time, making the algorithm best suited for high dimensional datasets. A proof is provided about the minimal I-map condition of the returned network, and also computational experiments are reported to show the gain with respect to CPU requirements.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Abellán, J., Gomez-Olmedo, M., Moral, S.: Some Variations on the PC Algorithm. In: Proc. of The third EuropeanWorkshop on Probabilistic Graphical Models (2006)
Acid, S., de Campos, L.M.: A hybrid methodology for learning belief networks: Benedict. International Journal of Approximate Reasoning 27(3), 235–262 (2001)
Acid, S., de Campos, L.M.: Searching for Bayesian Network Structures in the Space of Restricted Acyclic Partially Directed Graphs. Journal of Artificial Intelligence Research 18, 445–490 (2003)
de Campos, L.M.: A Scoring Function for Learning Bayesian Networks based on Mutual Information and Conditional Independence Tests. Journal of Machine Learning Research 7, 2149–2187 (2006)
de Campos, L.M., Fernández-Luna, J.M., Gámez, J.A., Puerta, J.M.: Ant colony optimization for learning Bayesian networks. International Journal of Approximate Reasoning 31, 291–311 (2002)
de Campos, L.M., Puerta, J.M.: Stochastic local search algorithms for learning belief networks: Searching in the space of orderings. In: Benferhat, S., Besnard, P. (eds.) ECSQARU 2001. LNCS (LNAI), vol. 2143, pp. 228–239. Springer, Heidelberg (2001)
de Campos, L.M., Puerta, J.M.: Local Search Methods for Learning Bayesian Networks Using a Modified Neighborhood in the Space of DAGs. In: Garijo, F.J., Riquelme, J.-C., Toro, M. (eds.) IBERAMIA 2002. LNCS (LNAI), vol. 2527, pp. 182–192. Springer, Heidelberg (2002)
Chickering, D.M.: Optimal structure identification with greedy search. Journal of Machine Learning Research 3, 507–554 (2002)
Chickering, D.M., Geiger, D., Heckerman, D.: Learning Bayesian networks is NPComplete. In: Fisher, D., Lenz, H. (eds.) Learning from Data: Artificial Intelligence and Statistics V, pp. 121–130. Springer, Heidelberg (1996)
van Dijk, S., van der Gaag, L.C., Thierens, D.: A Skeleton-Based Approach to Learning Bayesian Networks from Data. In: Lavrač, N., Gamberger, D., Todorovski, L., Blockeel, H. (eds.) PKDD 2003. LNCS (LNAI), vol. 2838, pp. 132–143. Springer, Heidelberg (2003)
Consortium, E.: Elvira: An Environment for Creating and Using Probabilistic Graphical Models. In: Proc. of the First European Workshop on Probabilistic Graphical Models, pp. 222–230 (2002)
Friedman, N., Geiger, D., Goldszmidt, M.: Bayesian network classifiers. Machine Learning 29, 131–163 (1997)
Friedman, N., Nachman, I., Peer, D.: Learning Bayesian networks from massive datasets: The sparse candidate algorithm. In: Proc. of the 15th Conf. on Uncertainty in Artificial Intelligence, pp. 201–210 (1999)
Heckerman, D., Geiger, D., Chickering, D.M.: Learning Bayesian networks: The combination of knowledge and statistical data. Machine Learning 20, 197–244 (1995)
Gámez, J.A., Puerta, J.M.: Constrained Score+(Local)Search Methods for Learning Bayesian Networks. In: Godo, L. (ed.) ECSQARU 2005. LNCS (LNAI), vol. 3571, pp. 161–173. Springer, Heidelberg (2005)
Jensen, F.V.: Bayesian Networks and Decision Graphs. Springer, Heidelberg (2001)
Neapolitan, R.: Learning Bayesian Networks. Prentice-Hall, Englewood Cliffs (2003)
Margaritis, D.: Learning Bayesian Model Structure from Data. Ph.D. thesis, School of Computer Science, Carnegie Mellon University (2003)
Moral, S.: An Empirical Comparison of Score Measures for Independence. In: Proc of the 10th IPMU International Conference, pp. 1307–1314 (2004)
Pearl, J.: Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Morgan Kaufmann, San Mateo (1988)
Spirtes, P., Glymour, C., Scheines, R.: Causation, Prediction, and Search. Lecture Notes in Statistics, vol. 81. Springer, Heidelberg (1993)
Tsamardinos, I., Brown, L.E., Aliferis, C.F.: The max-min hill-climbing Bayesian network structure learning algorithm. Machine Learning 65(1), 31–78 (2006)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2007 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Gámez, J.A., Mateo, J.L., Puerta, J.M. (2007). A Fast Hill-Climbing Algorithm for Bayesian Networks Structure Learning. In: Mellouli, K. (eds) Symbolic and Quantitative Approaches to Reasoning with Uncertainty. ECSQARU 2007. Lecture Notes in Computer Science(), vol 4724. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-75256-1_52
Download citation
DOI: https://doi.org/10.1007/978-3-540-75256-1_52
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-75255-4
Online ISBN: 978-3-540-75256-1
eBook Packages: Computer ScienceComputer Science (R0)