Skip to main content
Springer Nature Link
Log in

A Graph Theoretic Analysis of Double Base Number Systems

  • Conference paper
Progress in Cryptology – INDOCRYPT 2007 (INDOCRYPT 2007)

Part of the book series: Lecture Notes in Computer Science ((LNSC,volume 4859))

Included in the following conference series:

Abstract

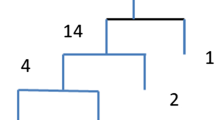
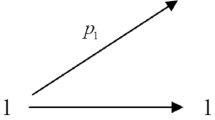
Double base number systems (DBNS) provide an elegant way to represent numbers. These representations also have many interesting and useful properties, which have been exploited to find many applications in Cryptography and Signal Processing. In the current article we present a scheme to represent numbers in double (and multi-) base format by combinatorial objects like graphs and diagraphs. The combinatorial representation leads to proof of some interesting results about the double and multibase representation of integers. These proofs are based on simple combinatorial arguments. In this article we have provided a graph theoretic proof of the recurrence relation satisfied by the number of double base representations of a given integer. The result has been further generalized to more than 2 bases. Also, we have uncovered some interesting properties of the sequence representing the number of double base representation of a positive integer n. It is expected that the combinatorial representation can serve as a tool for a better understanding of the double (and multi-) base number systems.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Avanzi, R.M., Sica, F.: Scalar Multiplication on Koblitz Curves using Double Bases. Available at http://eprint.iacr.org/2006/067.pdf

  2. Avanzi, R.M., Dimitrov, V., Doche, C., Sica, F.: Extending Scalar Multiplication to Double Bases. In: Lai, X., Chen, K. (eds.) ASIACRYPT 2006. LNCS, vol. 4284, pp. 130–144. Springer, Heidelberg (2006)

    Chapter  Google Scholar 

  3. Berth é, V., Imbert, L.: On converting numbers to the double-base number system. In: Luk, F.T. (ed.) Advanced Signal Processing Algorithms, Architecture and Implementations XIV, Proceedings of SPIE, vol. 5559, pp. 70–78. SPIE, San Jose, CA (2004)

    Google Scholar 

  4. Ciet, M., Lauter, K., Joye, M., Montgomery, P.L.: Trading inversions for multiplications in elliptic curve cryptography. Designs, Codes and Cryptography 39(2), 189–206 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  5. Bosma, W.: Signed bits and fast exponentiation. J. Theor. Nombres Bordeaux 13, 27–41 (2001)

    MATH  MathSciNet  Google Scholar 

  6. Ciet, M., Lauter, K., Joye, M., Montgomery, P.L.: Trading inversions for multiplications in elliptic curve cryptography. Designs, Codes and Cryptography 39(2), 189–206 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  7. Ciet, M., Sica, F.: An Analysis of Double Base Number Systems and a Sublinear Scalar Multiplication Algorithm. In: Dawson, E., Vaudenay, S. (eds.) Mycrypt 2005. LNCS, vol. 3715, pp. 171–182. Springer, Heidelberg (2005)

    Chapter  Google Scholar 

  8. de Weger, B.M.M.: Algorithms for Diophantine equations of CWI Tracts. In: Centrum voor Wiskunde en Informatica, Amsterdam (1989)

    Google Scholar 

  9. Dimitrov, V.S., Imbert, L., Mishra, P.K.: Efficient and secure elliptic curve point multiplication using double-base chains. In: Roy, B. (ed.) ASIACRYPT 2005. LNCS, vol. 3788, pp. 59–78. Springer, Heidelberg (2005)

    Chapter  Google Scholar 

  10. Dimitrov, V.S., Imbert, L., Mishra, P.K.: The Double Base Number System and Its Applications to Elliptic Curve Cryptography. Research Report LIRMM #06032 (May 2006)

    Google Scholar 

  11. Dimitrov, V., Järvinen, K.U., Jacobson, M.J., Chan, W.F., Huang, Z.: FPGA Implementation of Point Multiplication on Koblitz Curves Using Kleinian Integers. In: Goubin, L., Matsui, M. (eds.) CHES 2006. LNCS, vol. 4249, pp. 445–459. Springer, Heidelberg (2006)

    Chapter  Google Scholar 

  12. Dimitrov, V.S., Jullien, G.A., Miller, W.C.: An algorithm for modular exponentiation. Information Processing Letters 66(3), 155–159 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  13. Dimitrov, V.S., Jullien, G.A., Miller, W.C.: Theory and applications of the double-base number system. IEEE Transactions on Computers 48(10), 1098–1106 (1999)

    Article  Google Scholar 

  14. Doche, C., Imbert, L.: Extended Double-Base Number System with Applications to Elliptic Curve Cryptography. In: Barua, R., Lange, T. (eds.) INDOCRYPT 2006. LNCS, vol. 4329, pp. 335–348. Springer, Heidelberg (2006)

    Chapter  Google Scholar 

  15. Doche, C., Icart, T., Kohel, D.: Efficient Scalar Multiplication by Isogeny Decompositions. In: Yung, M., Dodis, Y., Kiayias, A., Malkin, T.G. (eds.) PKC 2006. LNCS, vol. 3958, pp. 191–206. Springer, Heidelberg (2006)

    Chapter  Google Scholar 

  16. Mahler, K.: On a Special Functional Equation. J of London Math Soc. 15, 115–123 (1939)

    Article  MathSciNet  Google Scholar 

  17. Mishra, P.K., Dimitrov, V.: Efficient Quintuple Formulas and Efficient Elliptic Curve Scalar Multiplication using Multibase Number Representation. In ISC (to appear, 2007)

    Google Scholar 

  18. Mishra, P.K., Dimitrov, V.: WIndow-based Elliptic CUrve Scalar Multiplication Using Double Base Number Representation. In Inscrypt (to appear, 2007)

    Google Scholar 

  19. Pennington, W.B.: On Mahler’s partition problem. Annals of Math. 57, 531–546 (1953)

    Article  MathSciNet  Google Scholar 

  20. Reitwiesner, G.: Binary Arithmetic. Adv. Comput. 1, 231–308 (1962)

    Google Scholar 

  21. Tijdeman, R.: On the maximal distance between integers composed of small primes. Compositio Mathematica 28, 159–162 (1974)

    MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Calgary, Calgary, AB, Canada

    Pradeep Kumar Mishra & Vassil Dimitrov

Authors
  1. Pradeep Kumar Mishra
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Vassil Dimitrov
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

K. Srinathan C. Pandu Rangan Moti Yung

Rights and permissions

Reprints and permissions

Copyright information

© 2007 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Mishra, P.K., Dimitrov, V. (2007). A Graph Theoretic Analysis of Double Base Number Systems. In: Srinathan, K., Rangan, C.P., Yung, M. (eds) Progress in Cryptology – INDOCRYPT 2007. INDOCRYPT 2007. Lecture Notes in Computer Science, vol 4859. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-77026-8_12

Download citation

  • DOI: https://doi.org/10.1007/978-3-540-77026-8_12

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-540-77025-1

  • Online ISBN: 978-3-540-77026-8

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics