Skip to main content
Springer Nature Link
Log in

Cyclotomic Mapping Permutation Polynomials over Finite Fields

  • Conference paper
Sequences, Subsequences, and Consequences

Part of the book series: Lecture Notes in Computer Science ((LNSC,volume 4893))

  • 835 Accesses

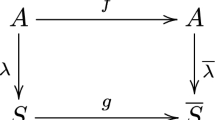
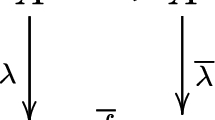Abstract

We explore a connection between permutation polynomials of the form x r f(x (q − 1)/l) and cyclotomic mapping permutation polynomials over finite fields. As an application, we characterize a class of permutation binomials in terms of generalized Lucas sequences.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Akbary, A., Alaric, S., Wang, Q.: On some classes of permutation polynomials. Int. J. Number Theory (to appear)

    Google Scholar 

  2. Akbary, A., Wang, Q.: On some permutation polynomials. Int. J. Math. Math. Sci. 16, 2631–2640 (2005)

    Article  MathSciNet  Google Scholar 

  3. Akbary, A., Wang, Q.: A generalized Lucas sequence and permutation binomials. Proc. Amer. Math. Soc. 134(1), 15–22 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  4. Akbary, A., Wang, Q.: On polynomials of the form x r f(x (q − 1)/l). Int. J. Math. Math. Sci. (to appear)

    Google Scholar 

  5. Bell, J., Wang, Q.: A note on Costas arrays and cyclotomic permutations. Ars Combin. (to appear)

    Google Scholar 

  6. Blackburn, S.R., Etzion, T., Paterson, K.G.: Permutation polynomials, de Bruijn sequences, and linear complexity. J. Combin. Theory Ser. A 76(1), 55–82 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  7. Chu, W., Colbourn, C.J., Dukes, P.: Constructions for permutation codes in powerline communications. Des. Codes Cryptogr. 32(1-3), 51–64 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  8. Chu, W., Golomb, S.W.: Circular Tuscan-k arrays from permutation binomials. J. Combin. Theory Ser. A 97(1), 195–202 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  9. Cohen, S.D.: Permutation group theory and permutation polynomials. In: Algebras and combinatorics (Hong Kong, 1997), pp. 133–146. Springer, Singapore (1999)

    Google Scholar 

  10. Evans, A.B.: Cyclotomy and orthomorphisms: A survey. Congr. Numer. 101, 97–107 (1994)

    MATH  MathSciNet  Google Scholar 

  11. Golomb, S.W., Moreno, O.: On periodicity properties of Costas arrays and a conjecture on permutation polynomials. IEEE Trans. Inform. Theory 42(6) part 2, 2252–2253 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  12. Levine, J., Brawley, J.V.: Some cryptographic applications of permutation polynomials. Cryptologia 1, 76–92 (1977)

    Article  Google Scholar 

  13. Levine, J., Chandler, R.: Some further cryptographic applications of permutation polynomials. Cryptologia 11, 211–218 (1987)

    Article  MathSciNet  Google Scholar 

  14. Lidl, R., Müller, W.B.: Permutation polynomials in RSA-cryptosystems. In: Adv. in Cryptology, Plenum, New York, pp. 293–301 (1984)

    Google Scholar 

  15. Lidl, R., Mullen, G.L.: When does a polynomial over a finite field permute the elements of the field? Amer. Math. Monthly 95, 243–246 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  16. Lidl, R., Mullen, G.L.: When does a polynomial over a finite field permute the elements of the field? II. Amer. Math. Monthly 100, 71–74 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  17. Lidl, R., Mullen, G.L., Turnwald, G.: Dickson polynomials. In: Pitman Monographs and Surveys in Pure and Applied Math., Longman, London/Harlow/Essex (1993)

    Google Scholar 

  18. Lidl, R., Niederreiter, H.: Finite Fields. In: Encyclopedia of Mathematics and Its Applications, Cambridge University Press, Cambridge (1997)

    Google Scholar 

  19. Mullen, G.L.: Permutation polynomials over finite fields. In: Finite Fields, Coding Theory, and Advances in Communications and Computing, pp. 131–151. Marcel Dekker, New York (1993)

    Google Scholar 

  20. Niederreiter, H., Winterhof, A.: Cyclotomic \(\mathcal{R}\)-orthomorphisms of finite fields. Discrete Math. 295, 161–171 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  21. Rivest, R.L.: Permutation polynomials modulo 2w. Finite fields Appl. 7, 287–292 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  22. Rivest, R.L., Robshaw, M.J.B., Sidney, R., Yin, Y.L.: The RC6 block cipher, Published electoronically at http://theory.lcs.mit.edu/rivest/rc6.pdf

  23. Rayes, M.O., Trevisan, V., Wang, P.: Factorization of Chebyshev polynomials, http://icm.mcs.kent.edu/reports/index1998.html

  24. Wan, D., Lidl, R.: Permutation polynomials of the form x r f(x (q − 1)/d) and their group structure. Monatsh. Math. 112, 149–163 (1991)

    Article  MATH  MathSciNet  Google Scholar 

  25. Wang, L.: On permutation polynomials. Finite Fields Appl. 8, 311–322 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  26. Sun, J., Takeshita, O.Y.: Interleavers for Turbo codes using permutation polynomials over integer rings. IEEE Trans. Inform. Theory 51(1), 101–119 (2005)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Carleton University, 1125 Colonel By Drive, Ottawa, Ontario, K1S 5B6, Canada

    Qiang Wang

Authors
  1. Qiang Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Solomon W. Golomb Guang Gong Tor Helleseth Hong-Yeop Song

Rights and permissions

Reprints and permissions

Copyright information

© 2007 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Wang, Q. (2007). Cyclotomic Mapping Permutation Polynomials over Finite Fields. In: Golomb, S.W., Gong, G., Helleseth, T., Song, HY. (eds) Sequences, Subsequences, and Consequences. Lecture Notes in Computer Science, vol 4893. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-77404-4_11

Download citation

  • DOI: https://doi.org/10.1007/978-3-540-77404-4_11

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-540-77403-7

  • Online ISBN: 978-3-540-77404-4

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics