Abstract
In recent years, considerable advances have been made in the study of properties of metric spaces in terms of their doubling dimension. This line of research has not only enhanced our understanding of finite metrics, but has also resulted in many algorithmic applications. However, we still do not understand the interaction between various graph-theoretic (topological) properties of graphs, and the doubling (geometric) properties of the shortest-path metrics induced by them. For instance, the following natural question suggests itself: given a finite doubling metric (V,d), is there always an unweighted graph (V′,E′) with V ⊆ V′ such that the shortest path metric d′ on V′ is still doubling, and which agrees with d on V . This is often useful, given that unweighted graphs are often easier to reason about.
A first hurdle to answering this question is that subdividing edges can increase the doubling dimension unboundedly, and it is not difficult to show that the answer to the above question is negative. However, surprisingly, allowing a  distortion between d and d′ enables us bypass this impossibility: we show that for any metric space (V,d), there is an unweighted graph (V′,E′) with shortest-path metric
distortion between d and d′ enables us bypass this impossibility: we show that for any metric space (V,d), there is an unweighted graph (V′,E′) with shortest-path metric  such that
such that
-
for all x,y ∈ V, the distances
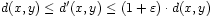 , and
, and -
the doubling dimension for d′ is not much more than that of d, where this change depends only on
 and not on the size of the graph.
and not on the size of the graph.
We show a similar result when both (V,d) and (V′,E′) are restricted to be trees: this gives a simple proof that doubling trees embed into constant dimensional Euclidean space with constant distortion. We also show that our results are tight in terms of the tradeoff between distortion and dimension blowup.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Assouad, P.: Plongements lipschitziens dans \({\bf R}\sp{n}\). Bull. Soc. Math. France 111(4), 429–448 (1983)
Beygelzimer, A., Kakade, S., Langford, J.: Cover trees for nearest neighbor. In: The 23rd International Conference on Machine Learning (ICML) (2006)
Călinescu, G., Karloff, H., Rabani, Y.: Approximation algorithms for the 0-extension problem. In: Proceedings of the twelfth annual ACM-SIAM symposium on Discrete algorithms, pp. 8–16. ACM Press, New York (2001)
Chan, H.T.-H., Gupta, A., Maggs, B.M., Zhou, S.: On hierarchical routing in DOubling metrics. In: Proceedings of the 16th ACM-SIAM Symposium on Discrete Algorithms (SODA), pp. 762–771 (2005)
Clarkson, K.L.: Nearest neighbor queries in metric spaces. Discrete Comput. Geom. 22(1), 63–93 (1999)
Cole, R., Gottlieb, L.-A.: Searching dynamic point sets in spaces with bounded doubling dimension. In: The thirty-eighth annual ACM symposium on Theory of computing (STOC) (2006)
Fakcharoenphol, J., Harrelson, C., Rao, S., Talwar, K.: An improved approximation algorithm for the 0-extension problem. In: Proceedings of the fourteenth annual ACM-SIAM symposium on Discrete algorithms, pp. 257–265. Society for Industrial and Applied Mathematics (2003)
Gupta, A., Krauthgamer, R., Lee, J.R.: Bounded geometries, fractals, and low–distortion embeddings. In: Proceedings of the 44th Symposium on the Foundations of Computer Science (FOCS), pp. 534–543 (2003)
Gupta, A., Newman, I., Rabinovich, Y., Sinclair, A.: Cuts, trees and ℓ1-embeddings of graphs. Combinatorica 24(2), 233–269 (2004) (Preliminary version in 40th FOCS 1999)
Gupta, A., Talwar, K.: How to complete a doubling metric (2008), http://arxiv.org/abs/0712.3331v1
Har-Peled, S., Mendel, M.: Fast constructions of nets in low dimensional metrics, and their applications. In: Proceedings of the twenty-first annual symposium on Computational geometry, pp. 150–158 (2005)
Indyk, P., Naor, A.: Nearest neighbor preserving embeddings. In: ACM Transactions on Algorithms (to appear)
Johnson, W.B., Lindenstrauss, J., Schechtman, G.: Extensions of lipschitz maps into banach spaces. Israel J. Math. 54(2), 129–138 (1986)
Karzanov, A.: Minimum 0-extensions of graph metrics. European Journal of Combinatorics 19(1), 71–101 (1998)
Klein, P., Plotkin, S.A., Rao, S.B.: Excluded minors, network decomposition, and multicommodity flow. In: Proceedings of the 25th ACM Symposium on the Theory of Computing (STOC), pp. 682–690 (1993)
Konjevod, G., Richa, A.W., Xia, D.: Optimal-stretch name-independent compact routing in doubling metrics. In: The twenty-fifth annual ACM symposium on Principles of distributed computing (2006)
Konjevod, G., Richa, A.W., Xia, D.: Optimal scale-free compact routing schemes in doubling networks. In: Proceedings of the 18th ACM-SIAM Symposium on Discrete Algorithms (SODA) (2007)
Krauthgamer, R., Lee, J.R.: The intrinsic dimensionality of graphs. In: Proceedings of the thirty-fifth annual ACM symposium on Theory of computing, pp. 438–447. ACM Press, New York (2003)
Krauthgamer, R., Lee, J.R.: Navigating nets: simple algorithms for proximity search. In: Proceedings of the fifteenth annual ACM-SIAM symposium on Discrete algorithms, pp. 798–807. Society for Industrial and Applied Mathematics (2004)
Lee, J., Naor, A.: Absolute lipschitz extendability. Comptes Rendus de l’Académie des Sciences - Series I - Mathematics 338(11), 859–862 (2004)
Lee, J., Naor, A., Peres, Y.: Trees and Markov convexity. Geometric and Functional Analysis. Preliminary version in SODA (to appear, 2006)
Matoušek, J.: On embedding trees into uniformly convex Banach spaces. Israel Journal of Mathematics 114, 221–237 (1999); (Czech version in: Lipschitz distance of metric spaces, C.Sc. degree thesis, Charles University 1990).
Matoušek, J.: Extension of Lipschitz mappings on metric trees. Commentationes Mathematicae Universitatis Carolinae 31(1), 99–104 (1990)
Rao, S.B.: Small distortion and volume preserving embeddings for planar and Euclidean metrics. In: 15th Annual ACM Symposium on Computational Geometry, pp. 300–306 (1999)
Talwar, K.: Bypassing the embedding: Algorithms for low-dimensional metrics. In: Proceedings of the 36th ACM Symposium on the Theory of Computing (STOC), pp. 281–290 (2004)
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 2008 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Gupta, A., Talwar, K. (2008). How to Complete a Doubling Metric. In: Laber, E.S., Bornstein, C., Nogueira, L.T., Faria, L. (eds) LATIN 2008: Theoretical Informatics. LATIN 2008. Lecture Notes in Computer Science, vol 4957. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-78773-0_4
Download citation
DOI: https://doi.org/10.1007/978-3-540-78773-0_4
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-78772-3
Online ISBN: 978-3-540-78773-0
eBook Packages: Computer ScienceComputer Science (R0)


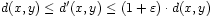 , and
, and and not on the size of the graph.
and not on the size of the graph.

