Abstract
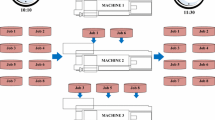
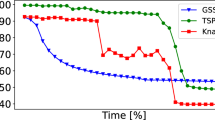
This paper presents a solution of a constrained two dimensional strip packing problem using genetic algorithms. The constraint consists of considering three-stage guillotine patterns. This is quite a real constraint motivated by technological considerations in some industries. An analysis of including distributed population ideas and parallelism into the basic genetic algorithm is carried out to solve the problem accurately and efficiently. Experimental evidence in this work shows that the proposed parallel versions of the distributed algorithms outperform their sequential counterparts in time, although there are no significant differences either in the mean best values obtained or in the effort.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Alba, E.: Parallel evolutionary algorithms can achieve super-linear performance. Information Processing Letters 82(1), 7–13 (2002)
Alba, E.: Parallel Metaheuristics: A New Class of Algorithms. Wiley, Chichester (2005)
Alba, E., et al.: MALLBA: A Library of Skeletons for Combinatorial Optimisation. In: Monien, B., Feldmann, R.L. (eds.) Euro-Par 2002. LNCS, vol. 2400, pp. 63–73. Springer, Heidelberg (2002)
Bäck, T., Fogel, D., Michalewicz, Z.: Handbook of Evolutionary Computation. Oxford University Press, New York (1997)
Bortfeldt, A.: A genetic algorithm for the two-dimensional strip packing problem with rectangular pieces. EJOR 172(3), 814–837 (2006)
Hopper, E., Turton, B.: An empirical investigation of meta-heuristic and heuristic algorithms for a 2D packing problem. EJOR 128(1), 4–57 (2000)
Lodi, A., Martello, S., Monaci, M.: Recent advances on two-dimensional bin packing problems. Discrete Applied Mathematics 123, 379–396 (2002)
Michalewicz, M.: Genetic Algorithms + Data Structures = Evolution Programs, 3rd edn. Springer, Heidelberg (1996)
Mumford-Valenzuela, C.L., Vick, J., Wang, P.Y.: Metaheuristics: Computer Decision-Making. In: Chapter Heuristics for large strip packing problems with guillotine patterns: An empirical study, pp. 501–522 (2003)
Puchinger, J., Raidl, G.R.: Models and algorithms for three-stage two-dimensional bin packing. Technical Report TR-186-04-04, Technische Universität Wien, Institut für Computergraphik und Algorithmen (2004)
Puchinger, J., Raidl, G.R., Koller, G.: Solving a Real-World Glass Cutting Problem. In: Gottlieb, J., Raidl, G.R. (eds.) EvoCOP 2004. LNCS, vol. 3004, pp. 165–176. Springer, Heidelberg (2004)
Salto, C., Molina, J.M., Alba, E.: Sequential versus distributed evolutionary approaches for the two-dimensional guillotine cutting problem. In: Proc. of International Conference on Industrial Logistics, pp. 291–300 (2005)
Salto, C., Molina, J.M., Alba, E.: Analysis of distributed genetic algorithms for solving cutting problems. ITOR 13(5), 403–423 (2006)
Salto, C., Molina, J.M., Alba, E.: A comparison of different recombination operators for the 2-dimensional strip packing problem. In: Proc. of the XII Congreso Argentino de Ciencias de la Computación, pp. 1126–1138 (2006)
Salto, C., Molina, J.M., Alba, E.: Evolutionary algorithms for the level strip packing problem. In: Proc. of the Workshop on Nature Inspired Cooperative Strategies for Optimization, pp. 137–148 (2006)
Spiessens, P., Manderick, B.: A massevily parallel genetic algorithm. In: Proc. of the 4th. International Conference on Genetic Algorithms, pp. 279–286 (1991)
Tanese, R.: Distributed genetic algorithms. In: Proc. of the 3rd. International Conference on Genetic Algorithms, pp. 434–439 (1989)
Wang, P.Y., Valenzuela, C.L.: Data set generation for rectangular placement problems. EJOR 134, 378–391 (2001)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2008 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Salto, C., Alba, E., Molina, J.M. (2008). Analysis of Distributed Genetic Algorithms for Solving a Strip Packing Problem. In: Lirkov, I., Margenov, S., Waśniewski, J. (eds) Large-Scale Scientific Computing. LSSC 2007. Lecture Notes in Computer Science, vol 4818. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-78827-0_70
Download citation
DOI: https://doi.org/10.1007/978-3-540-78827-0_70
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-78825-6
Online ISBN: 978-3-540-78827-0
eBook Packages: Computer ScienceComputer Science (R0)