Skip to main content
Springer Nature Link
Log in

Approximating Optimal Binary Decision Trees

  • Conference paper
Approximation, Randomization and Combinatorial Optimization. Algorithms and Techniques (APPROX 2008, RANDOM 2008)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 5171))

Abstract

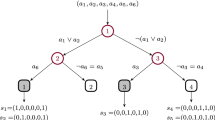
We give a (ln n + 1)-approximation for the decision tree (DT) problem. An instance of DT is a set of m binary tests T = (T 1, ..., T m ) and a set of n items X = (X 1, ..., X n ). The goal is to output a binary tree where each internal node is a test, each leaf is an item and the total external path length of the tree is minimized. Total external path length is the sum of the depths of all the leaves in the tree. DT has a long history in computer science with applications ranging from medical diagnosis to experiment design. It also generalizes the problem of finding optimal average-case search strategies in partially ordered sets which includes several alphabetic tree problems. Our work decreases the previous upper bound on the approximation ratio by a constant factor. We provide a new analysis of the greedy algorithm that uses a simple accounting scheme to spread the cost of a tree among pairs of items split at a particular node. We conclude by showing that our upper bound also holds for the DT problem with weighted tests.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Alekhnovich, M., Braverman, M., Feldman, V., Klivans, A.R., Pitassi, T.: Learnability and automatizability. In: Proceedings of the 45th Annual Symposium on Foundations of Computer Science, pp. 621–630. IEEE Computer Society Press, Los Alamitos (2004)

    Chapter  Google Scholar 

  2. Arkin, E.M., Meijer, H., Mitchell, J.S.B., Rappaport, D., Skiena, S.: Decision trees for geometric models. International Journal of Computational Geometry and Applications 8(3), 343–364 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  3. Carmo, R., Donadelli, J., Kohayakawa, Y., Laber, E.S.: Searching in random partially ordered sets. Theor. Comput. Sci. 321(1), 41–57 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  4. Chakaravarthy, V.T., Pandit, V., Roy, S., Awasthi, P., Mohania, M.K.: Decision trees for entity identification: approximation algorithms and hardness results. In: Libkin, L. (ed.) Proceedings of the Twenty-Sixth ACM Symposium on Principles of Database Systems, pp. 53–62 (2007)

    Google Scholar 

  5. Feige, U., Lovász, L., Tetali, P.: Approximating min-sum set cover. Algorithmica 40(4), 219–234 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  6. Garey, M.R.: Optimal binary identification procedures. SIAM Journal on Applied Mathematics 23(2), 173–186 (1972)

    Article  MATH  MathSciNet  Google Scholar 

  7. Garey, M.R., Graham, R.L.: Performance bounds on the splitting algorithm for binary testing. Acta Inf. 3, 347–355 (1974)

    MATH  MathSciNet  Google Scholar 

  8. Garey, M.R., Johnson, D.S.: Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman, New York (1979)

    MATH  Google Scholar 

  9. Hancock, T., Jiang, T., Li, M., Tromp, J.: Lower bounds on learning decision lists and trees. Information and Computation 126(2), 114–122 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  10. Heeringa, B.: Improving Access to Organized Information. PhD thesis. University of Massachusetts, Amherst (2006)

    Google Scholar 

  11. Hyafil, L., Rivest, R.: Constructing optimal binary decision trees is np-complete. Information Processing Letters 5(1), 15–17 (1976)

    Article  MATH  MathSciNet  Google Scholar 

  12. Rao Kosaraju, S., Przytycka, T.M., Borgstrom, R.S.: On an optimal split tree problem. In: Dehne, F.K.H.A., Gupta, A., Sack, J.-R., Tamassia, R. (eds.) WADS 1999. LNCS, vol. 1663, pp. 157–168. Springer, Heidelberg (1999)

    Chapter  Google Scholar 

  13. Laber, E.S., Nogueira, L.T.: On the hardness of the minimum height decision tree problem. Discrete Applied Mathematics 144(1-2), 209–212 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  14. Moret, B.M.E.: Decision trees and diagrams. ACM Comput. Surv. 14(4), 593–623 (1982)

    Article  Google Scholar 

  15. Moshkov, M.J.: Greedy algorithm of decision tree construction for real data tables. In: Transactions on Rough Sets, pp. 161–168 (2004)

    Google Scholar 

  16. Munagala, K., Babu, S., Motwani, R., Widom, J.: The pipelined set cover problem. In: ICDT, pp. 83–98 (2005)

    Google Scholar 

  17. Murthy, K.V.S.: On growing better decision trees from data. PhD thesis, The Johns Hopkins University (1996)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science, University of Massachusetts, Amherst, 140 Governors Drive, Amherst, MA 01003

    Micah Adler

  2. Department of Computer Science, Williams College, 47 Lab Campus Drive, Williamstown, MA 01267

    Brent Heeringa

Authors
  1. Micah Adler
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Brent Heeringa
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Ashish Goel Klaus Jansen José D. P. Rolim Ronitt Rubinfeld

Rights and permissions

Reprints and permissions

Copyright information

© 2008 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Adler, M., Heeringa, B. (2008). Approximating Optimal Binary Decision Trees. In: Goel, A., Jansen, K., Rolim, J.D.P., Rubinfeld, R. (eds) Approximation, Randomization and Combinatorial Optimization. Algorithms and Techniques. APPROX RANDOM 2008 2008. Lecture Notes in Computer Science, vol 5171. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-85363-3_1

Download citation

  • DOI: https://doi.org/10.1007/978-3-540-85363-3_1

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-540-85362-6

  • Online ISBN: 978-3-540-85363-3

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics