Abstract
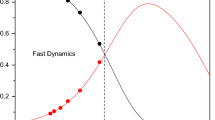
Kinetic models for biochemical systems often comprise a large amount of coupled differential equations with species concentrations varying on different time scales. In this paper we present and apply two novel methods aimed at automatic complexity and model reduction by numerical algorithms. The first method combines dynamic sensitivity analysis with singular value decomposition. The aim is to determine the minimal dimension of the kinetic model necessary to describe the active dynamics of the system accurately enough within a user-defined error tolerance for particular species concentrations and to determine each species’ contribution to the active dynamics. The second method treats the explicit numerical reduction of the model to a lower dimension according to the results of the first method and allows any species combination to be chosen as a parameterization of the reduced model which may either be tabulated in the form of look-up tables or computed in situ during numerical simulations. A reduced representation of a multiple time scale system is particularly beneficial in the context of spatiotemporal simulations which require high computational efforts. Both the complexity analysis and model reduction method operate in a fully automatic and numerically highly efficient way and have been implemented in a software package. The methods are applied to a biochemical example model describing the ERK signaling pathway. With this example, we demonstrate the value of the methods for various applications in systems biology.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Bauer, I., Finocchi, F., Duschl, W.J., Gail, H.-P., Schlöder, J.P.: Simulation of chemical reactions and dust destruction in protoplanetary accretion discs. Astron. Astrophys. 317, 273–289 (1997)
Bock, H.G.: Numerical treatment of inverse problems in chemical reaction kinetics. In: Ebert, K.H., Deuflhard, P., Jäger, W. (eds.) Modeling of Chemical Reaction Systems. Springer Series in Chemical Physics, vol. 18, pp. 102–125. Springer, Heidelberg (1981)
Bock, H.G.: Randwertproblemmethoden zur Parameteridentifizierung in Systemen nichlinearer Differentialgleichungen. Bonner Mathematische Schriften, vol. 183. University of Bonn, Bonn (1987)
Bock, H.G., Plitt, K.J.: A multiple shooting algorithm for direct solution of optimal control problems. In: Proc. 9th IFAC World Congress Budapest. Pergamon Press, Oxford (1984)
Bodenstein, M.: Eine Theorie der photochemischen Reaktionsgeschwindigkeiten. Z. Phys. Chem. 85, 329–397 (1913)
Chapman, D., Underhill, L.: The interaction of chlorine and hydrogen. The influence of mass. J. Chem. Soc. Trans. 103, 496–508 (1913)
Cho, K.-H., Shin, S.-Y., Kim, H.-W., Wolkenhauer, O., McFerran, B., Kolch, W.: Mathematical modeling of the influence of RKIP on the ERK signaling pathway. In: Priami, C. (ed.) CMSB 2003. LNCS, vol. 2602, pp. 127–141. Springer, Heidelberg (2003)
de Donder, T., van Rysselberghe, P.: Thermodynamic Theory of Affinity: A Book of Principles. Stanford University, Menlo Park (1936)
Gorban, A., Karlin, I.: Invariant Manifolds for Physical and Chemical Kinetics. Springer - Lecture Notes in Physics, vol. 660. Springer, Heidelberg (2005)
Gorban, A., Karlin, I., Zinovyev, A.: Constructive methods of invariant manifolds for kinetic problems. Phys. Rep. 396, 197–403 (2004)
Hadjinicolaou, M., Goussis, D.A.: Asymptotic solutions of stiff PDEs with the CSP method: the reaction diffusion equation. SIAM J. Sci. Comput. 20, 781–810 (1999)
Lam, S.H., Goussis, D.A.: The CSP method for simplifying kinetics. J. Chem. Kinet. 26, 461–486 (1994)
Lebiedz, D.: Computing minimal entropy production trajectories: An approach to model reduction in chemical kinetics. J. Chem. Phys. 120, 6890–6897 (2004)
Lebiedz, D., Kammerer, J., Brandt-Pollmann, U.: Automatic network coupling analysis for dynamical systems based on detailed kinetic models. Phys. Rev. E 72(041911) (2005)
Leineweber, D.B.: Efficient reduced SQP methods for the optimization of chemical processes described by large sparse DAE models. Fortschritt-Berichte VDI Reihe 3, Verfahrenstechnik, vol. 613. VDI-Verlag GmbH, Düsseldorf (1999)
Leineweber, D.B., Schäfer, A., Bock, H.G., Schlöder, J.P.: An efficient multiple shooting based reduced SQP strategy for large-scale dynamic process optimization – part I: Theoretical aspects. Comput. Chem. Engng. 27, 157–166 (2003)
Leineweber, D.B., Schäfer, A., Bock, H.G., Schlöder, J.P.: An efficient multiple shooting based reduced SQP strategy for large-scale dynamic process optimization – part II: Software aspects and applications. Comput. Chem. Engng. 27, 167–174 (2003)
Li, G., Pope, S.B., Rabitz, H.: New approaches to determination of constrained lumping schemes for a reaction system in the whole composition space. Chem. Eng. Sci. 46, 95–111 (1991)
Maas, U.: Coupling of chemical reaction with flow and molecular transport. Appl. Math. 40, 249–266 (1995)
Maas, U.: Efficient calculation of intrinsic low-dimensional manifolds for the simplification of chemical kinetics. Springer – Computing and Visualization in Science 1, 69–81 (1998)
Maas, U., Pope, S.B.: Simplifying chemical kinetics: Intrinsic low-dimensional manifolds in composition space. Combust. Flame 88, 239–264 (1992)
Michaelis, L., Menten, M.L.: Die Kinetik der Invertinwirkung. Biochem. Z. 49, 333–369 (1913)
Okino, M.S., Mavrovouniotis, M.L.: Simplification of mathematical models of chemical systems. Chem. Rev. 98, 391–406 (1998)
Petrov, V., Nikolova, E., Wolkenhauer, O.: Reduction of nonlinear dynamic systems with an application to signal transduction pathways. IET Syst. Biol. 1(1), 2–9 (2007)
Rabitz, H., Kramer, M., Dacol, D.: Sensitivity analysis in chemical kinetics. Annu. Rev. Phys. Chem. 34, 419–461 (1983)
Reinhardt, V., Winckler, M., Lebiedz, D.: Approximation of slow attracting manifolds by trajectory-based optimization approaches. J. Phys. Chem. A 112, 1712–1718 (2008)
Shaik, O.S., Kammerer, J., Górecki, J., Lebiedz, D.: Derivation of a quantitative minimal model for the photosensitive Belousov-Zhabotinsky reaction from a detailed elementary-step mechanism. J. Chem. Phys. 123(234103) (2005)
Tomlin, A.S., Pilling, M.J., Turányi, T., Merkin, J.H., Brindley, J.: Mechanism reduction for the oscillatory oxidation of hydrogen sensitivity and quasi-steady state analyses. Combust. Flame 91, 107–130 (1992)
Trefethen, L.N., Bau, D.: Numerical Linear Algebra. SIAM, Philadelphia (1997)
Turányi, T.: Sensitivity analysis of complex kinetic systems. Tools and applications. J. Math. Chem. 5, 203–248 (1990)
Warnatz, J., Maas, U., Dibble, R.W.: Combustion. Physical and Chemical Fundamentals, Modeling and Simulation, Experiments, Pollutant Formation, 3rd edn. Springer, Heidelberg (2001)
Zobeley, J., Lebiedz, D., Kammerer, J., Ishmurzin, A., Kummer, U.: A new time-dependent complexity reduction method for biological systems. Trans. Comput. Syst. Biol. 1, 90–110 (2005)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2008 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Lebiedz, D., Skanda, D., Fein, M. (2008). Automatic Complexity Analysis and Model Reduction of Nonlinear Biochemical Systems. In: Heiner, M., Uhrmacher, A.M. (eds) Computational Methods in Systems Biology. CMSB 2008. Lecture Notes in Computer Science(), vol 5307. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-88562-7_12
Download citation
DOI: https://doi.org/10.1007/978-3-540-88562-7_12
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-88561-0
Online ISBN: 978-3-540-88562-7
eBook Packages: Computer ScienceComputer Science (R0)