Abstract
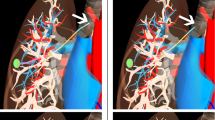
Steerable needles can be used in medical applications to reach targets behind sensitive or impenetrable areas. The kinematics of a steerable needle are nonholonomic and, in 2D, equivalent to a Dubins car with constant radius of curvature. In 3D, the needle can be interpreted as an airplane with constant speed and pitch rate, zero yaw, and controllable roll angle.
We present a constant-time motion planning algorithm for steerable needles based on explicit geometric inverse kinematics similar to the classic Paden-Kahan subproblems. Reachability and path competitivity are analyzed using analytic comparisons with shortest path solutions for the Dubins car (for 2D) and numerical simulations (for 3D). We also present an algorithm for local path adaptation using null-space results from redundant manipulator theory. The inverse kinematics algorithm can be used as a fast local planner for global motion planning in environments with obstacles, either fully autonomously or in a computer-assisted setting.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Alterovitz, R., Branicky, M., Goldberg, K.: Constant-curvature motion planning under uncertainty with applications in image-guided medical needle steering. In: Proceedings of Workshop on the Algorithmic Foundations of Robotics (July 2006)
Alterovitz, R., Goldberg, K., Okamura, A.: Planning for steerable bevel-tip needle insertion through 2D soft tissue with obstacles. In: Proceedings of the IEEE International Conference on Robotics and Automation, April 2005, pp. 1640–1645 (2005)
Alterovitz, R., Siméon, T., Goldberg, K.: The stochastic motion roadmap: A sampling framework for planning with Markov motion uncertainty. In: Proceedings of Robotics: Science and Systems (June 2007)
DiMaio, S., Salcudean, S.: Needle steering and motion planning in soft tissues. IEEE Transactions on Biomedical Engineering 52(6), 965–974 (2005)
Dubins, L.: On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents. American Journal of Mathematics 79(3), 497–516 (1957)
Duindam, V., Alterovitz, R., Sastry, S., Goldberg, K.: Screw-based motion planning for bevel-tip flexible needles in 3D environments with obstacles. In: Proceedings of the IEEE International Conference on Robotics and Automation, May 2008, pp. 2483–2488 (2008)
Engh, J., Podnar, G., Kondziolka, D., Riviere, C.: Toward effective needle steering in brain tissue. In: Proc. 28th Annu. Intl. Conf. IEEE Eng. Med. Biol. Soc., pp. 559–562 (2006)
Gabriely, Y., Rimon, E.: Competitive Complexity of Mobile Robot On Line Motion Planning Problems. In: Algorithmic Foundations of Robotics VI. STAR, vol. 17, pp. 155–170. Springer, Heidelberg (2005)
Icking, C., Klein, R.: Competitive strategies for autonomous systems. In: Modelling and Planning for Sensor Based Intelligent Robot Systems, pp. 23–40 (1995)
Kallem, V., Cowan, N.: Image-guided control of flexible bevel-tip needles. In: Proceedings of the IEEE International Conference on Robotics and Automation, April 2007, pp. 3015–3020 (2007)
Kavraki, L., Švestka, P., Latombe, J., Overmars, M.: Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Transactions on Robotics and Automation 12(4), 566–580 (1996)
Minhas, D., Engh, J., Fenske, M., Riviere, C.: Modeling of needle steering via duty-cycled spinning. In: Proceedings of the International Conference of the IEEE EMBS Cité Internationale, August 2007, pp. 2756–2759 (2007)
Murray, R., Li, Z., Sastry, S.: A Mathematical Introduction to Robotic Manipulation. CRC Press, Boca Raton (1994)
Park, W., Kim, J., Zhou, Y., Cowan, N., Okamura, A., Chirikjian, G.: Diffusion-based motion planning for a nonholonomic flexible needle model. In: Proceedings of the IEEE International Conference on Robotics and Automation, April 2005, pp. 4611–4616 (2005)
Park, W., Liu, Y., Zhou, Y., Moses, M., Chirikjian, G.: Kinematic state estimation and motion planning for stochastic nonholonomic systems using the exponential map. Robotica 26, 419–434 (2008)
Webster III, R., Kim, J., Cowan, N., Chirikjian, G., Okamura, A.: Nonholonomic modeling of needle steering. International Journal of Robotics Research 5/6, 509–525 (2006)
Webster III, R., Memisevic, J., Okamura, A.: Design considerations for robotic needle steering. In: Proceedings of the IEEE International Conference on Robotics and Automation, April 2005, pp. 3588–3594 (2005)
Webster III, R., Okamura, A., Cowan, N., Chirikjian, G., Goldberg, K., Alterovitz, R.: Distal bevel-tip needle control device and algorithm. US patent pending 11/436,995 (May 2006)
Xu, J., Duindam, V., Alterovitz, R., Goldberg, K.: Motion planning for steerable needles in 3D environments with obstacles using rapidly-exploring random trees and backchaining. In: Proceedings of the IEEE Conference on Automation Science and Engineering, August 2008, pp. 41–46 (2008)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2009 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Duindam, V., Xu, J., Alterovitz, R., Sastry, S., Goldberg, K. (2009). 3D Motion Planning Algorithms for Steerable Needles Using Inverse Kinematics. In: Chirikjian, G.S., Choset, H., Morales, M., Murphey, T. (eds) Algorithmic Foundation of Robotics VIII. Springer Tracts in Advanced Robotics, vol 57. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-00312-7_33
Download citation
DOI: https://doi.org/10.1007/978-3-642-00312-7_33
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-00311-0
Online ISBN: 978-3-642-00312-7
eBook Packages: EngineeringEngineering (R0)