Skip to main content
Springer Nature Link
Log in

Images as Symbols: An Associative Neurotransmitter-Field Model of the Brodmann Areas

  • Chapter
Transactions on Computational Science V

Part of the book series: Lecture Notes in Computer Science ((TCOMPUTATSCIE,volume 5540))

Abstract

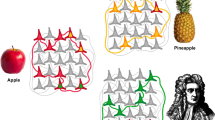
The ability to associate images is the basis for learning relationships involving vision, hearing, tactile sensation, and kinetic motion. A new architecture is described that has only local, recurrent connections, but can directly form global image associations. This architecture has many similarities to the structure of the cerebral cortex, including the division into Brodmann areas, the distinct internal and external lamina, and the pattern of neuron interconnection. The images are represented as neurotransmitter fields, which differ from neural fields in the underlying principle that the state variables are not the neuron action potentials, but the chemical concentration of neurotransmitters in the extracellular space. The neurotransmitter cloud hypothesis, which asserts that functions of space, time and frequency, are encoded by the density of identifiable molecules, allows the abstract mathematical power of cellular processing to be extended by incorporating a new chemical model of computation. This makes it possible for a small number of neurons, even a single neuron, to establish an association between arbitrary images. A single layer of neurons, in effect, performs the computation of a two-layer neural network.

Analogous to the bits in an SR flip-flop, two arbitrary images can hold each other in place in an association processor and thereby form a short-term image memory. Just as the reciprocal voltage levels in a flip-flop can produce a dynamical system with two stable states, reciprocal-image pairs can generate stable attractors thereby allowing the images to serve as symbols. Spherically symmetric wavelets, identical to those found in the receptive fields of the retina, enable efficient image computations. Noise reduction in the continuous wavelet transform representations is possible using an orthogonal projection based on the reproducing kernel. Experimental results demonstrating stable reciprocalimage attractors are presented.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Brodmann, K.: Vergleichende Lokalisationslehre der Grosshirnrinde in ihren Prinzipien dargestellt auf Grund des Zellenbaues. Barth, Leipzig (1909)

    Google Scholar 

  2. Kandel, E.R., Schwartz, J.H., Jessell, T.M.: Principles of Neural Science, 4th edn. McGraw-Hill, New York (2000)

    Google Scholar 

  3. Garoutte, B.: Survey of Functional Neuroanatomy, 3rd edn. Mill Valley Medical, California (1994)

    Google Scholar 

  4. Spivak, M.: A Comprehensive Introduction to Differential Geometry, 3rd edn. Publish or Perish, Wilmington (1979)

    MATH  Google Scholar 

  5. Schutz, B.: Geometric Methods of Mathematical Physics. Cambridge University Press, Cambridge (1980)

    Book  MATH  Google Scholar 

  6. Knudsen, E.I., du Lac, S., Esterly, S.D.: Computational Maps in the Brain. Ann. Rev. of Neuroscience 10, 41–65 (1987)

    Article  Google Scholar 

  7. Greer, D.S.: A Unified System of Computational Manifolds. Tech. Rep. TR-CIS-0602-03, Dept. of Comp. and Info. Sci., IUPUI, Indianapolis (2003)

    Google Scholar 

  8. Monad, J.: Chance and Necessity: An Essay on the Natural Philosophy of Modern Biology (Trans. A. Wainhouse). Knopf, New York (1971)

    Google Scholar 

  9. Mallat, S.: A Wavelet Tour of Signal Processing, 2nd edn. Academic Press, San Diego (1999)

    MATH  Google Scholar 

  10. Wang, Y.: The Cognitive Processes of Abstraction and Formal Inferences. In: Proc. 4th IEEE International Conf. on Cognitive Informatics, Irvine, California (2005)

    Google Scholar 

  11. Wang, Y.: The Theoretical Framework of Cognitive Informatics. International J. of Cognitive Informatics and Natural Intelligence 1(1), 1–27 (2007)

    Article  MathSciNet  Google Scholar 

  12. Yao, Y.Y.: Concept Formation and Learning: a Cognitive Informatics Perspective. In: Proc. 3rd IEEE International Conf. on Cognitive Informatics, Victoria, Canada (2004)

    Google Scholar 

  13. Prince, V., Lafourcade, M.: Mixing Semantic Networks and Conceptual Vectors Application to Hyperonymy. IEEE Trans. Systems, Man and Cybernetics, C 36, 152–160 (2006)

    Article  Google Scholar 

  14. Willshaw, D.J., Buneman, O.P., Longuet-Higgins, H.C.: Non-holographic Associative Memory. Nature 222, 960–962 (1969)

    Article  Google Scholar 

  15. Kosko, B.: Bidirectional Associative Memories. IEEE Trans. Systems, Man and Cybernetics 18, 49–60 (1988)

    Article  MathSciNet  Google Scholar 

  16. Xu, Z., Leung, Y., He, X.: Asymmetrical Bidirectional Associative Memories. IEEE Trans. Systems, Man, and Cybernetics 24, 1558–1564 (1994)

    Article  Google Scholar 

  17. Chua, L.O., Yang, L.: Cellular Neural Networks: Theory. IEEE Trans. Circuits and Systems 35(10), 1257–1272 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  18. Zhang, Q., Benveniste, A.: Wavelet Networks. IEEE Trans. Neural Networks 3(6), 889–898 (1992)

    Article  Google Scholar 

  19. Thuillard, M.: A Review of Wavelet Networks, Wavenets, Fuzzy Wavenets and their Applications. In: Advances in Computational Intelligence and Learning: Methods and Applications. Kluwer, Deventer (2002)

    Google Scholar 

  20. Iyengar, S.S., Cho, E.C., Phoha, V.V.: Foundations of Wavelet Networks and Applications. CRC, Boca Raton (2002)

    Google Scholar 

  21. Beurle, R.L.: Properties of a Mass of Cells Capable of Regenerating Pulses. Philosophical Trans. of the Royal Society. Series B 240, 55–94 (1956)

    Article  Google Scholar 

  22. Griffith, J.S.: A Field Theory of Neural Nets: I: Derivation of Field Equations. Bulletin of Mathematical Biophysics 25, 111–120 (1963)

    Article  MathSciNet  MATH  Google Scholar 

  23. Griffith, J.S.: A Field Theory of Neural Nets: II. Properties of the Field Equations. Bulletin of Mathematical Biophysics 27, 187–195 (1965)

    Article  MathSciNet  MATH  Google Scholar 

  24. Amari, S.: Dynamics of Pattern Formation in the Lateral-Inhibition Type Neural Fields. Biological Cybernetics 27, 77–87 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  25. Ermentrout, B.: Neural Networks as Spatio-temporal Pattern-Forming Systems. Reports on Progress in Physics 61, 353–430 (1998)

    Article  Google Scholar 

  26. Vogels, T.P., Rajan, K., Abbott, L.F.: Neural Network Dynamics. Annual Rev. Neuroscience 28, 357–376 (2005)

    Article  Google Scholar 

  27. Sarnat, H.B., Netsky, M.G.: Evolution of the Nervous System, 2nd edn. Oxford (1981)

    Google Scholar 

  28. Widrow, B., Hoff, M.E.: Adaptive Switching Circuits. WESCON Convention Record, pp. 96–104. IRE, New York (1960)

    Google Scholar 

  29. Royden, H.L.: Real Analysis, 3rd edn. Prentice-Hall, Englewood Cliffs (1988)

    MATH  Google Scholar 

  30. Greer, D.S.: Neurotransmitter Fields. In: Proc. of International Conf. on Artificial Neural Networks, Porto, Portugal (2007)

    Google Scholar 

  31. Bishop, C.M.: Neural Networks for Pattern Recognition. Oxford University Press, Oxford (1995)

    MATH  Google Scholar 

  32. Thompson, J.M.T., Stewart, H.B.: Nonlinear Dynamics and Chaos. Wiley, Hoboken (2002)

    MATH  Google Scholar 

  33. Nevatia, R.: Machine Perception. Prentice-Hall, Englewood Cliffs (1982)

    Google Scholar 

  34. Churchland, P., Sejnowski, T.J.: The Computational Brain. MIT Press, Cambridge (1994)

    Google Scholar 

  35. Daubechies, I.: Ten Lectures on Wavelets. Society for Industrial and Applied Mathematics, Philadelphia (1992)

    Google Scholar 

  36. Addison, P.S.: The Illustrated Wavelet Transform Handbook. Institute of Physics Publishing, Bristol (2002)

    Google Scholar 

  37. Aronszajn, N.: Theory of Reproducing Kernels. Trans. of the American Mathematical Society 68(3), 337–404 (1950)

    Article  MathSciNet  MATH  Google Scholar 

  38. Saitoh, S.: Integral Transforms, Reproducing Kernels and their Applications. Addison Wesley Longman, Essex (1997)

    Google Scholar 

  39. Thompson, K.: Alpha Blending. In: Glassner, A. (ed.) Graphics Gems, pp. 210–211. Academic Press, Cambridge (1990)

    Chapter  Google Scholar 

  40. von Economo, G.N., Koskinas, G.N.: The Cytoarchitectonics of the Adult Human Cortex (trans. H. L. Seldon). Springer, Heidelberg (1925)

    Google Scholar 

  41. Greer, D.S.: The Computational Manifold Approach to Consciousness and Symbolic Processing in the Cerebral Cortex. In: Proc. 7th IEEE International Conference on Cognitive Informatics (2008)

    Google Scholar 

  42. Behrens, T.E.J., Johansen-Berg, W.H.M.W., Smith, S.M., Wheeler-Kingshott, C.A.M., Boulby, P.A., et al.: Non-invasive Mapping of Connections between Human Thalamus and Cortex Using Diffusion Imaging. Nature Neuroscience 6(7), 750–757 (2003)

    Article  Google Scholar 

  43. Robinson, J.C.: Infinite-Dimensional Dynamical Systems: An Introduction to Dissipative Parabolic PDEs and the Theory of Global Attractors. Cambridge University Press, Cambridge (2001)

    Book  MATH  Google Scholar 

  44. Greer, D.S.: Sapphire 0.4 Implementation Notes. Tech. Rep. TR-CIS-0714-08, Dept. of Comp. and Info. Sci., IUPUI, Indianapolis (2008)

    Google Scholar 

  45. Computational Results, http://www.gmanif.com/results.html

Download references

Author information

Authors and Affiliations

  1. General Manifolds, Carlsbad, California, USA

    Douglas S. Greer

Authors
  1. Douglas S. Greer
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. University of Calgary, Department of Computer Science, 2500 University Drive N.W, T2N 1N4, Calgary, AB, Canada

    Marina L. Gavrilova

  2. OptimaNumerics Ltd., Cathedral House, 23-31 Waring Street, BT1 2DX, Belfast, UK

    C. J. Kenneth Tan

  3. Theoretical and Empirical Software Engineering Research Centre (TESERC), University of Calgary, 2500 University Drive, NW, T2N 1N4, Calgary, Alberta, Canada

    Yingxu Wang

  4. Department of Computing, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong

    Keith C. C. Chan

Rights and permissions

Reprints and permissions

Copyright information

© 2009 Springer-Verlag Berlin Heidelberg

About this chapter

Cite this chapter

Greer, D.S. (2009). Images as Symbols: An Associative Neurotransmitter-Field Model of the Brodmann Areas. In: Gavrilova, M.L., Tan, C.J.K., Wang, Y., Chan, K.C.C. (eds) Transactions on Computational Science V. Lecture Notes in Computer Science, vol 5540. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-02097-1_3

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-02097-1_3

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-02096-4

  • Online ISBN: 978-3-642-02097-1

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics