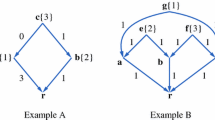
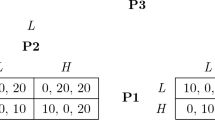
Abstract
We study restricted improvement cycles (ri-cycles) in finite positional n-person games with perfect information modeled by directed graphs (digraphs) that may contain cycles. We obtain criteria of restricted improvement acyclicity (ri-acyclicity) in two cases: for n = 2 and for acyclic digraphs. We provide several examples that outline the limits of these criteria and show that, essentially, there are no other ri-acyclic cases. We also discuss connections between ri-acyclicity and some open problems related to Nash-solvability.
The full version of this paper with complete proofs is available as the research report, [1]. This research was supported by the Center for Algorithmic Game Theory at Aarhus University, funded by the Carlsberg Foundation. The second author was partially supported also by DIMACS, Center for Discrete Mathematics and Theoretical Computer Science, Rutgers University, and by Graduate School of Information Science and Technology, University of Tokyo.
This is a preview of subscription content, log in via an institution to check access.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Andersson, D., Gurvich, V., Hansen, T.D.: On acyclicity of games with cycles. DIMACS Technical Report 2009-09, Rutgers University
Boros, E., Gurvich, V.: On Nash-solvability in pure strategies of finite games with perfect information which have cycles. Math. Social Sciences 46 (2003)
Boros, E., Gurvich, V., Makino, K., Shao, W.: Nash-solvable bidirected cyclic two-person game forms, Rutcor Research Report 26-2007 and DIMACS Technical Report 2008-13, Rutgers University
Edmonds, J., Fulkerson, D.R.: Bottleneck Extrema, RM-5375-PR, The Rand Corporation, Santa Monica, Ca. (January 1968); J. Combin. Theory 8, 299–306 (1970)
Gimbert, H., Sørensen, T.B.: Private communications (July 2008)
Gurvich, V.: To theory of multi-step games USSR Comput. Math. and Math. Phys. 13(6), 143–161 (1973)
Gurvich, V.: Solution of positional games in pure strategies. USSR Comput. Math. and Math. Phys. 15(2), 74–87 (1975)
Gurvich, V.: Equilibrium in pure strategies. Soviet Mathematics Doklady 38(3), 597–602 (1988)
Kukushkin, N.S.: Perfect information and potential games. Games and Economic Behavior 38, 306–317 (2002)
Kukushkin, N.S.: Acyclicity of improvements in finite game forms (manuscript, 2009), http://www.ccas.ru/mmes/mmeda/ququ/GF.pdf
Kukushkin, N.S.: Private communications (August 2008)
Zermelo, E.: Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels. In: Proc. 5th Int. Cong. Math. Cambridge 1912, vol. II, pp. 501–504. Cambridge University Press, Cambridge (1913)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2009 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Andersson, D., Gurvich, V., Hansen, T.D. (2009). On Acyclicity of Games with Cycles. In: Goldberg, A.V., Zhou, Y. (eds) Algorithmic Aspects in Information and Management. AAIM 2009. Lecture Notes in Computer Science, vol 5564. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-02158-9_4
Download citation
DOI: https://doi.org/10.1007/978-3-642-02158-9_4
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-02157-2
Online ISBN: 978-3-642-02158-9
eBook Packages: Computer ScienceComputer Science (R0)