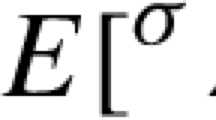Abstract
In this paper, we study the Kelly criterion in the continuous time framework building on the work of E.O. Thorp and others. The existence of an optimal strategy is proven in a general setting and the corresponding optimal wealth process is found. A simple formula is provided for calculating the optimal portfolio for a set of price processes satisfying some simple conditions. Properties of the optimal investment strategy for assets governed by multiple Ornstein-Uhlenbeck processes are studied. The paper ends with a short discus-sion of the implications of these ideas for financial markets.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Kelly, J.L.: A New Interpretation of Information Rate. Bell System Technical Journal 35, 917–926 (1956)
Thorp, E.O.: The Kelly Criterion in Blackjack, Sports Betting, and the Stock Market. In: The 10th International Conference on Gambling and Risk Taking (1997)
Breiman, L.: Optimal Gambling Systems for Favorable Games. In: Neyman, J. (ed.) Proceedings of the Berkeley Symposium on Mathematical Statistics and Probability, vol. 1, pp. 65–78 (1961)
Kargin, V.: Optimal Convergence Trading, arXiv: math.OC/0302104 (2003)
Musiela, M., Rutkowski, M.: Martingale Methods in Financial Modelling. Springer, New York (1997)
Karatzas, I., Shreve, S.: Brownian Motion and Stochastic Calculus. Springer, Heidelberg (1998)
Lv, Y., Meister, B.K., Peters, O.: Implications of the Kelly Criterion for Multiple Ornstein-Uhlenbeck Processes. In: Bachelier Finance Society Fifth World Congress (2008)
Hakansson, N.H.: On Optimal Myopic Portfolio Policies, with and without Serial Correlation of Yields. Journal of Business 44, 324–334 (1971)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2009 ICST Institute for Computer Science, Social Informatics and Telecommunications Engineering
About this paper
Cite this paper
Lv, Y., Meister, B.K. (2009). Application of the Kelly Criterion to Ornstein-Uhlenbeck Processes. In: Zhou, J. (eds) Complex Sciences. Complex 2009. Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering, vol 4. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-02466-5_105
Download citation
DOI: https://doi.org/10.1007/978-3-642-02466-5_105
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-02465-8
Online ISBN: 978-3-642-02466-5
eBook Packages: Computer ScienceComputer Science (R0)