Abstract
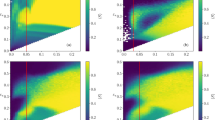
In this paper, we study the opinion dynamics of Improved Deffuant model (IDM), where the convergence parameter μ is a function of the opposite’s degree K according to the celebrity effect, in small-world network (SWN) and scale-free network (SFN). Generically, the system undergoes a phase transition from the plurality state to the polarization state and to the consensus state as the confidence parameter ε increasing. Furthermore, the evolution of the steady opinion s * as a function of ε, and the relation between the minority steady opinion \(s_{*}^{min}\) and the individual connectivity k also have been analyzed. Our present work shows the crucial role of the confidence parameter and the complex system topology in the opinion dynamics of IDM.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Liljeros, F., Edling, C.R., Amaral, L.A.N., Stanley, H.E., Aberg, Y.: The web of human sexual contacts. Nature 411, 907 (2001)
Watts, D.J., Strogatz, S.H.: Collective dynamics of ’small-world’ networks. Nature 393, 440 (1998)
Barabási, A.-L., Albert, R.: Emergence of Scaling in Random Networks. Science 286, 509 (1999)
Newman, M.E.J.: The structure of scientific collaboration networks. Proc. Natl. Acad. Sci. U.S.A. 98, 404 (2001)
Barabási, A.-L., Jeong, H., Néda, Z., Ravasz, E., Schubert, A., Vicsek, T.: Evolution of the social network of scientific collaborations. Physica A 311, 590 (2002)
Csányi, G., Szendrői, B.: Structure of a large social network. Phys. Rev. E 69, 036131 (2004)
Wang, F., Moreno, Y., Sun, Y.: Structure of peer-to-peer social networks. Phys. Rev. E 73, 036123 (2006)
Goh, K.-I., Eom, Y.-H., Jeong, H., Kahng, B., Kim, D.: Structure and evolution of online social relationships: Heterogeneity in unrestricted discussions. Phys. Rev. E 73, 066123 (2006)
Latané, B.: The psychology of social impact. American Psychologist 36, 343 (1981)
Latané, B., Wolf, S.: The social impact of majorities and minorities. Psychological Review 88, 438 (1981)
Sznajd-Weron, K., Sznajd, J.: Opinion evolution in closed community. Int. J. Mod. Phys. C 11, 1157 (2000)
Deffuant, G., Neau, D., Amblard, F., Weisbuch, G.: Mixing beliefs among interacting agents. Adv. Complex Systems 3, 87 (2000)
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., Hwang, D.-U.: Complex networks: structure and dynamics. Phys. Rep. 424, 175 (2006)
Albert, R., Barabási, A.-L.: Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47 (2002)
Porfiri, M., Bollt, E.M., Stilwell, D.J.: Decline of minorities in stubborn societies. Eur. Phys. J. B 57, 481 (2007)
Weisbuch, G., Dedduant, G., Amblard, F.: Persuasion dynamics. Physica A 353, 555 (2005)
Kozma, B., Barrat, A.: Consensus formation on adaptive networks. Phys. Rev. E 77, 016102 (2008)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2009 ICST Institute for Computer Science, Social Informatics and Telecommunications Engineering
About this paper
Cite this paper
Guo, L., Cai, X. (2009). Bifurcation Phenomena of Opinion Dynamics in Complex Networks. In: Zhou, J. (eds) Complex Sciences. Complex 2009. Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering, vol 4. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-02466-5_114
Download citation
DOI: https://doi.org/10.1007/978-3-642-02466-5_114
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-02465-8
Online ISBN: 978-3-642-02466-5
eBook Packages: Computer ScienceComputer Science (R0)