Abstract
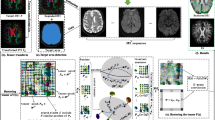
We denoise HARDI (High Angular Resolution Diffusion Imaging) data arising in medical imaging. Diffusion imaging is a relatively new and powerful method to measure the 3D profile of water diffusion at each point. This can be used to reconstruct fiber directions and pathways in the living brain, providing detailed maps of fiber integrity and connectivity. HARDI is a powerful new extension of diffusion imaging, which goes beyond the diffusion tensor imaging (DTI) model: mathematically, intensity data is given at every voxel and at any direction on the sphere. However, HARDI data is usually highly contaminated with noise, depending on the b-value which is a tuning parameter pre-selected to collect the data. Larger b-values help to collect more accurate information in terms of measuring diffusivity, but more noise is generated by many factors as well. So large b-values are preferred, if we can satisfactorily reduce the noise without losing the data structure. We propose a variational method to denoise HARDI data by denoising the spherical Apparent Diffusion Coefficient (sADC), a field of radial functions derived from the data. We use vectorial total variation regularization, an L 1 data fidelity term and the logarithmic barrier function in the minimization. We present experiments of denoising synthetic and real HARDI data.
Funded by the NIH Roadmap for Medical Research Grant U54 RR021813 (CCB).
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Alliney, S.: Digital Filters as Absolute Norm Regularizers. IEEE TSP 40(6), 1548–1562 (1992)
Barmpoutis, A., Jian, B., Vemuri, B.C., Shepherd, T.M.: Symmetric positive 4th order tensors & their estimation from diffusion weighted MRI. In: Karssemeijer, N., Lelieveldt, B. (eds.) IPMI 2007. LNCS, vol. 4584, pp. 308–319. Springer, Heidelberg (2007)
Basser, P.J., Pierpaoli, C.: Microstructural and physiological features of tissues elucidated by quantitative diffusion tensor MRI. JMR 111, 209–219 (1996)
Beaulieu, C., Allen, P.S.: Water diffusion in the giant axon of the squid: Implications for diffusion-weighted MRI of the nervous system. MRM 32(5), 579–583 (1994)
Blomgren, P.: Total Variation Methods for Restoration of Vector Valued Images (Ph.D. thesis), UCLA CAM Report 98-30 (1998)
Blomgren, P., Chan, T.F.: Color TV: Total variation methods for restoration of vector-valued images. IEEE TIP 7(3), 304–309 (1998)
Jonasson, L., Hagmann, P., Bresson, X., Thiran, J.-P., Wedeen, V.J.: Representing Diffusion MRI in 5D for Segmentation of White Matter Tracts with a Level Set Method. In: Christensen, G.E., Sonka, M. (eds.) IPMI 2005. LNCS, vol. 3565, pp. 311–320. Springer, Heidelberg (2005)
Chiang, M.C., Klunder, A.D., McMahon, K., de Zubicaray, G.I., Wright, M., Toga, A.W., Thompson, P.M.: Information-theoretic analysis of brain white matter fiber orientation distribution functions. In: Karssemeijer, N., Lelieveldt, B. (eds.) IPMI 2007. LNCS, vol. 4584, pp. 172–182. Springer, Heidelberg (2007)
Chiang, M.C., Leow, A.D., Dutton, R.A., Barysheva, M., Rose, S., McMahon, K.L., de Zubicaray, G.I., Toga, A.W., Thompson, P.M.: Fluid Registration of Diffusion Tensor Images Using Information Theory. IEEE TMI 2008 27(4), 442–456 (2008)
Cihangiroglu, M., Uluğ, A.M., Firat, Z., Bayram, A., Kovanlikaya, A., Kovanlikaya, İ.: High b-value diffusion-weighted MR imaging of normal brain at 3T. European Journal of Radiology 69(3), 454–458 (2009)
Deputte, S., Dierckx, H., Fieremans, E., D’Asseler, Y., Achten, R., Lemahieu, I.: Postprocessing of brain white matter fiber orientation distribution functions. In: Proc. IEEE ISBI: from Nano to Macro, pp. 784–787 (2007)
Descoteaux, M., Deriche, R.: High Angular Resolution Diffusion MRI Segmentation Using Region-Based Statistical Surface Evolution. JMIV 33(2), 239–252 (2009)
Descoteaux, M., Angelino, E., Fitzgibbons, S., Deriche, R.: Regularized, Fast and Robust Analytical Q-Ball Imaging. MRM 58(3), 497–510 (2007)
Descoteaux, M., Deriche, R.: Mapping neuronal fiber crossings in the human brain. SPIE Newsroom (August 2008)
Frank, L.R.: Characterization of anisotropy in high angular resolution diffusion-weighted MRI. MRM 47(6), 1083–1099 (2002)
Haro, G., Lenglet, C., Sapiro, G., Thompson, P.M.: On the Non-Uniform Complexity of Brain Connectivity. In: IEEE ISBI: from Nano to Macro, pp. 887–890 (2008)
Jian, B., Vemuri, B.C.: A Unified Computational Framework for Deconvolution to Reconstruct Multiple Fibers From Diffusion Weighted MRI. IEEE TMI 26(11), 1464–1471 (2007)
Jian, B., Vemuri, B.C., Özarslan, E., Carney, P.R., Mareci, T.H.: A novel tensor distribution model for the diffusion-weighted MR signal. NeuroImage 37(1), 164–176 (2007)
Jones, D.K., Horsfield, M.A., Simmons, A.: Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. MRM 42, 515–525 (1999)
Le Bihan, D., Breton, E.: Imagerie de diffusion in vivo par resonance magnétique nucléaire. CRAS 301, 1109–1112 (1985)
Le Bihan, D., Breton, E., Lallemand, D., Grenier, P., Cabanis, E., Laval-Jeantet, M.: MR imaging of intravoxel incoherent motions: Application to diffusion and perfusion in neurologic disorders. Radiology 161, 401–407 (1986)
Le Bihan, D., Poupon, C., Amadon, A., Lethimonnier, F.: Artifacts and Pitfalls in Diffusion MRI. JMRI 24, 478–488 (2006)
Lenglet, C., Campbell, J.S.W., Descoteaux, M., Haro, G., Savadjiev, P., Wassermann, D., Anwander, A., Deriche, R., Pike, G.B., Sapiro, G., Siddiqi, K., Thompson, P.M.: Mathematical Methods for Diffusion MRI Processing. NeuroImage. In: Thompson, P.M., Miller, M.I., Poldrack, R., Nichols, T. (eds.) Special Issue on Mathematics in Brain Imaging, November 13 (2008)
Leow, A.D., Zhu, S., Zhan, L., McMahon, K., de Zubicaray, G.I., Meredith, M., Wright, M.J., Toga, A.W., Thompson, P.M.: The Tensor Distribution Function. MRM 61(1), 205–214 (2008)
McGraw, T., Özarslan, E., Vemuri, B.C., Chen, Y., Mareci, T.: Denoising and visualization of HARDI data. REP-2005-360, CISE, Univ. of Florida (2005)
McGraw, T., Vemuri, B.C., Yezierski, B., Mareci, T.: Segmentation of High Angular Resolution Diffusion MRI Modeled as a Field of von Mises-Fisher Mixtures. In: Leonardis, A., Bischof, H., Pinz, A. (eds.) ECCV 2006. LNCS, vol. 3953, pp. 463–475. Springer, Heidelberg (2006)
McGraw, T., Vemuri, B.C., Yezierski, B., Mareci, T.: von Mises-Fisher Mixture model of the diffusion ODF. In: ISBI 2006: From Nano to Macro, pp. 65–68 (2006)
Merboldt, M., Hanicke, W., Frahm, J.: Self-diffusion NMR imaging using stimulated echoes. JMR 64, 479–486 (1985)
Nocedal, J., Wright, S.J.: Numerical Optimization. Springer Series in Operations Research. Springer, Heidelberg (1999)
Özarslan, E., Vemuri, B.C., Mareci, T.H.: Generalized scalar measures for diffusion MRI using trace, variance and entropy. MRM 53(4), 866–876 (2005)
Rudin, L.I., Osher, S., Fatemi, E.: Nonlinear total variation based noise removal algorithms. Physica D 60(1-4), 259–268 (1992)
Srivastava, A., Jermyn, I., Joshi, S.: Riemannian Analysis of Probability Density Functions with Application in Vision. In: IEEE CVPR, pp. 1–8 (2007)
Stejskal, E.O., Tanner, J.E.: Spin diffusion measurements: Spin echoes in the presence of a time-dependent field gradient. Journal of Chemical Physics 42, 288–292 (1965)
Tschumperlé, D.: PDE-Based Regularization of Multivalued Images and Applications. PhD Thesis Univ. of Nice-Sophia Antipolis, France (2002)
Tschumperlé, D., Deriche, R.: Anisotropic Diffusion Partial Differential Equations in Multi-Channel Image Processing: Framework and Applications. In: Book chapter in Advances in Imaging and Electron Physics (AIEP). Academic Press, London (2007)
Tschumperlé, D., Deriche, R.: Vector-Valued Image Regularization with PDE’s: A Common Framework for Different Applications. IEEE TPAMI 27(4), 506–517 (2005)
Tuch, D.S.: Diffusion MRI of Complex Tissue Structure. Ph. D. Thesis, Harvard-MIT Division of Health Sciences and Technology (2002)
Tuch, D.S., Weisskoff, R.M., Belliveau, J.W., Wedeen, V.J.: High angular resolution diffusion imaging of the human brain. In: Proc. 7th Annual Meeting of ISMRM, Philadelphia, PA, p. 321 (1999)
Tuch, D.S., Reese, T.G., Wiegell, M.R., Makris, N., Belliveau, J.W., Wedeen, V.J.: High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. MRM 48, 577–582 (2002)
Tuch, D.S., Reese, T.G., Wiegell, M.R., Wedeen, V.J.: Diffusion MRI of complex neural architecture. Neuron 40, 885–895 (2003)
Tuch, D.S.: Q-ball imaging. MRM 52, 1358–1372 (2004)
Verma, R., Khurd, P., Davatzikos, C.: On Analyzing Diffusion Tensor Images by Identifying Manifold Structure Using Isomaps. IEEE TMI 26(6), 772–778 (2007)
Wedeen, V.J., Hagmann, P., Tseng, W.Y., Reese, T.G., Weisskoff, R.M.: Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn. Reson. Med. 54(6), 1377–1386 (2005)
Zhan, L., Chiang, M.C., Barysheva, M., Toga, A.W., McMahon, K.L., de Zubicaray, G.I., Meredith, M., Wright, M.J., Thompson, P.M.: How Many Gradients are Sufficient in High-Angular Resolution Diffusion Imaging (HARDI)? In: MICCAI 2008, MICCAI DTI Workshop (2008)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2009 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Kim, Y., Thompson, P.M., Toga, A.W., Vese, L., Zhan, L. (2009). HARDI Denoising: Variational Regularization of the Spherical Apparent Diffusion Coefficient sADC . In: Prince, J.L., Pham, D.L., Myers, K.J. (eds) Information Processing in Medical Imaging. IPMI 2009. Lecture Notes in Computer Science, vol 5636. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-02498-6_43
Download citation
DOI: https://doi.org/10.1007/978-3-642-02498-6_43
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-02497-9
Online ISBN: 978-3-642-02498-6
eBook Packages: Computer ScienceComputer Science (R0)