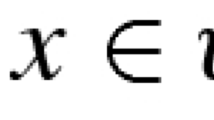Skip to main content
SpringerLink
Log in

Characterizations of Iterated Admissibility Based on PEGL

  • Conference paper
Logic, Rationality, and Interaction (LORI 2009)

Part of the book series: Lecture Notes in Computer Science ((LNAI,volume 5834))

Included in the following conference series:

  • 623 Accesses

Abstract

Iterated dominance is perhaps the most basic principle in game theory. The epistemic foundation of this principle is based on the assumption that all players are rational. The main contribution of this paper is to characterize the algorithm of iterated admissibility in Probabilistic Epistemic Game Logic (PEGL). Firstly, on the basis of Probabilistic Epistemic Logic we set up a logic PEGL. Secondly, by redefining a concept of rationality, we show that the common knowledge of the rationality characterizes the algorithm of Iterated Admissibility, that is, we provide an epistemic foundation for the solutions or equilibria which are found by the algorithm of Iterated Admissibility(IA). Next, we provide a different characterization of IA using public announcements of the rationality in dynamic logic. The results we obtain can be seen as giving a dynamic epistemic foundation for the algorithm of Iterated Admissibility.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 39.99
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 54.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

References

  1. Aumann, R.J.: Rationality and bounded rationality. Games and Economic Behavior 53, 293–391 (1999)

    MATH  Google Scholar 

  2. Brandenburger, A., Friedenberg, A., Keisler, H.J.: Admissibility in games. Econometrica 76(2), 307–352 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  3. Gilli, M.: Iterated admissibility as solution concept in game theory. Technical report, University of Milano-Bicocca, Department of Economics (2002)

    Google Scholar 

  4. Rubinstein, A.: Modeling Bounded Rationality. MIT Press, Cambridge (1998)

    Google Scholar 

  5. Bernheim, D.: Rationalizable strategic behavior. Econometrica 52(4), 1007–1028 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  6. David, P.: Rationalizable strategic behavior and the problem of perfection. Econometrica 52(4), 1029–1050 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  7. van Benthem, J.: Rational dynamics and epistemic logic in games. International Game Theory Review 9(1), 13–45 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bonanno, G.: A syntactic approach to rationality in games with ordinal payoffs, vol. 3. Amsterdam University Press, Amsterdam (2008)

    MATH  Google Scholar 

  9. de Bruin, B.: Explaining Games: On the Logic of Game Theoretic Explanations. PhD thesis, Institute for logic, Language and Computation, Universiteit van Amsterdam, Amsterdam, The Netherlands (2004)

    Google Scholar 

  10. Fagin, R., Halpern, J.Y.: Reasoning about knowledge and probability. Journal of the ACM 41, 340–367 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  11. Cui, J.Y.: A method for solving nash equilibrium of game based on public announcement logic. Logics for Dynamics of Information and Preferences (2009), http://www.illc.uva.nl/lgc/seminar/?page_id=292

  12. Brandenburger, A.: Forward induction. Technical report, Stern School of Business, University of New York (2007)

    Google Scholar 

  13. Kooi, B.P.: Knowledge, Chance and Change. PhD thesis, Institute for logic, Language and Computation, Universiteit van Amsterdam, Amsterdam, The Netherlands (2004)

    Google Scholar 

  14. Blackburn, P., van Benthem, J., Wolter, F.: Handbook of Modal Logic. Elsevier Science Inc., Amsterdam (2007)

    MATH  Google Scholar 

  15. Shimoji, M.: On forward induction in money-burning games. Economic Theory 19(3), 637–648 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  16. Apt, K.R., Zvesper, J.A.: Common beliefs and public announcements in strategic games with arbitrary strategy sets. Journal of Logic and Computation (2007), http://www.citebase.org/abstract?id=oai:arXiv.org:0710.3536

  17. Christian, E.: Iterated weak dominance in strictly competitive games of perfect information. Games and Economic Behavior (2002)

    Google Scholar 

  18. van Benthem, J.: Decisions, actions and game, a logical perspective. Technical report, ILLC, University of Amsterdam and Department of Philosophy, Stanford University (2008), http://staff.science.uva.nl/~johan/Chennai.ICLA3.pdf

  19. Apt, K.R.: Relative strength of strategy elimination procedures. Economics Bulletin 3 (2007)

    Google Scholar 

  20. Ebbinghaus, H.D., Flum, J.: Finite Model Theory. Springer, Berlin (1995)

    MATH  Google Scholar 

  21. Stalnaker, R.: Extensive and strategic form: Games and models for games. Research in Economics 21, 2–14 (1997)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Logic and Intelligence, Southwest University, Tiansheng road. 2, BeibBei district, 400715, Chongqing, P.R. China

    Jianying Cui, Meiyun Guo & Xiaojia Tang

Authors
  1. Jianying Cui
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Meiyun Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiaojia Tang
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Institute of Logic and Intelligence, Southwest University, 2, Tiansheng Road, 400715, Chongqing, China

    Xiangdong He

  2. Philosophy Department, University of Maryland, Institute for Advanced Computer Studies (UMIACS), 20742, College Park, MD, USA

    John Horty

  3. Center for Logic and Philosophy of Science, Tilburg University, Dante Building, 5000, Tilburg, LE, The Netherlands

    Eric Pacuit

Rights and permissions

Reprints and permissions

Copyright information

© 2009 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Cui, J., Guo, M., Tang, X. (2009). Characterizations of Iterated Admissibility Based on PEGL. In: He, X., Horty, J., Pacuit, E. (eds) Logic, Rationality, and Interaction. LORI 2009. Lecture Notes in Computer Science(), vol 5834. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-04893-7_7

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-04893-7_7

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-04892-0

  • Online ISBN: 978-3-642-04893-7

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics

Search

Navigation