Abstract
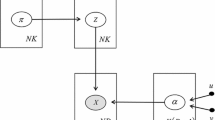
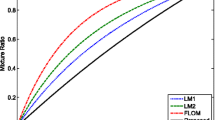
In this paper we present improvements to our Bayesian approach for describing the position distribution of the endocardium in cardiac ultrasound image sequences. The problem is represented as a latent variable model, which represents the inside and outside of the endocardium, for which the posterior density is estimated. We start our construction by assuming a three-component Rayleigh mixture model: for blood, echocardiographic artifacts, and tissue. The Rayleigh distribution has been previously shown to be a suitable model for blood and tissue in cardiac ultrasound images. From the mixture model parameters we build a latent variable model, with two realizations: tissue and endocardium. The model is refined by incorporating priors for spatial and temporal smoothness, in the form of total variation, connectivity, preferred shapes and position, by using the principal components and location distribution of manually segmented training shapes. The posterior density is sampled by a Gibbs method to estimate the expected latent variable image which we call the Bayesian Probability Map, since it describes the probability of pixels being classified as either heart tissue or within the endocardium. By sampling the translation distribution of the latent variables, we improve the convergence rate of the algorithm. Our experiments show promising results indicating the usefulness of the Bayesian Probability Maps for the clinician since, instead of producing a single segmenting curve, it highlights the uncertain areas and suggests possible segmentations.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Burckhardt, C.B.: Speckle in Ultrasound B-Mode Scans. IEEE Trans. Sonics and Ultrasonics 25, 1–6 (1978)
Wagner, R.F., Smith, S.W., Sandrik, J.M., Lopez, H.: Statistics of Speckle in Ultrasound B-Scans. IEEE Trans. Sonics and Ultrasonics 30, 156–163 (1983)
Goodman, J.: Laser Speckle and Related Phenomenon. Springer, New York (1975)
Tao, Z., Tagare, H., Beaty, J.: Evaluation of four probability distribution models for speckle in clinical cardiac ultrasound images. MedImg 25, 1483–1491 (2006)
Noble, J.A., Boukerroui, D.: Ultrasound image segmentation: A survey. IEEE Transactions on Medical Imaging 25, 987–1010 (2006)
Friedland, N., Adam, D.: Automatic ventricular cavity boundary detection from sequential ultrasound images using simulated anneal. IEEE Trans. Med. Imag. 8, 344–353 (1989)
Boukerroui, D., Baskurt, A., Noble, J.A., Basset, O.: Segmentation of ultrasound images: multiresolution 2d and 3d algorithm based on global and local statistics. Pattern Recogn. Lett. 24, 779–790 (2003)
Dias, J.M.B., Leitao, J.M.N.: Wall position and thickness estimation from sequences of echocardiographic images. IEEE Trans. Med. Imag 15, 25–38 (1996)
Song, M., Haralick, R., Sheehan, F., Johnson, R.: Integrated surface model optimization for freehand three-dimensional echocardiography. IEEE Transactions on Medical Imaging 21, 1077–1090 (2002)
Xiao, G., Brady, J.M., Noble, A.J., Zhang, Y.: Contrast enhancement and segmentation of ultrasound images: a statistical method. Medical Imaging 2000: Image Processing 3979, 1116–1125 (2000)
Figueiredo, M., Leitao, J.: Bayesian estimation of ventricular contours in angiographic images. IEEE Transactions on Medical Imaging 11, 416–429 (1992)
Hansson, M., Brandt, S., Gudmundsson, P.: Bayesian probability maps for the evaluation of cardiac ultrasound data. In: MICCAI Workshop: Probabilistic Models for Medical Image Analysis (2009)
Tikhonov, A.: Solutions of Ill Posed Problems. Vh Winston, Scripta series in mathematics (1977)
Dempster, A.P., Laird, N.M., Rubin, D.B.: Maximum likelihood form incomplete data via the EM algorithm (with discussion). J. R. Statist. Soc. Ser. B-Stat. Methodol. 39, 1–38 (1977)
Geman, S., Geman, D.: Stochastic relaxation, gibbs distributions, and the bayesian restoration of images. IEEE Trans. Pattern Analysis and Machine Intelligence 6, 721–741 (1984)
MacKay, D.: Information Theory, Inference and Learning Algorithms. Cambridge University Press, Cambridge (2003), http://www.inference.phy.cam.ac.uk/mackay/itila/book.html
Boykov, Y., Veksler, O., Zabih, R.: Fast approximate energy minimization via graph cuts. IEEE Trans. Pattern Analysis and Machine Intelligence 20, 1222–1239 (2001)
Kolmogorov, V., Zabih, R.: What energy functions can be minimized via graph cuts? IEEE Trans. Pattern Analysis and Machine Intelligence 26, 147–159 (2004)
Boykov, Y., Kolmogorov, V.: An experimental comparison of min-cut/max-flow algorithms. IEEE Trans. Pattern Analysis and Machine Intelligence 26, 1124–1137 (2004)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2009 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Hansson, M., Brandt, S., Gudmundsson, P., Lindgren, F. (2009). Evaluation of Cardiac Ultrasound Data by Bayesian Probability Maps. In: Bebis, G., et al. Advances in Visual Computing. ISVC 2009. Lecture Notes in Computer Science, vol 5876. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-10520-3_103
Download citation
DOI: https://doi.org/10.1007/978-3-642-10520-3_103
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-10519-7
Online ISBN: 978-3-642-10520-3
eBook Packages: Computer ScienceComputer Science (R0)