On Linear Programming Decoding on a Quantized Additive White Gaussian Noise Channel

Abstract

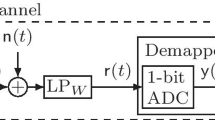
In this work, we consider the pairwise error probability (PEP) of a linear programming (LP) decoder for a general binary linear code as formulated by Feldman et al. (IEEE Trans. Inf. Theory, March 2005) on a quantized additive white Gaussian noise (AWGN) channel. With a quantized AWGN (QAWGN) channel, we mean a channel where we first compute log-likelihood ratios as for an AWGN channel and then quantize them. Let H be a parity-check matrix of a binary linear code and consider LP decoding based on H. The output of the LP decoder is always a pseudo-codeword, of some pseudo-weight, where the definition of pseudo-weight is specific to the underlying channel model. In this work, we give a definition of pseudo-weight for a QAWGN channel based on an asymptotic (high signal-to-noise ratio) analysis of the PEP. Note that with maximum-likelihood decoding, the parameters of the quantization scheme, i.e., the quantization levels and the corresponding quantization region thresholds, that minimize the PEP of wrongly decoding to a non-zero codeword c when the all-zero codeword is transmitted is independent of the specific codeword c. However, this is not the case with LP decoding based on a parity-check matrix H, which means that the quantization scheme needs to be optimized for the given H. As a case study, we consider the well-known (3,5)-regular (155,64,20) Tanner code and estimate its minimum QAWGN pseudo-weight with 3 and 5 levels of quantization, in which the quantization scheme is optimized to maximize the minimum QAWGN pseudo-weight.