Skip to main content
Springer Nature Link
Log in

Fast Arc-Annotated Subsequence Matching in Linear Space

  • Conference paper
SOFSEM 2010: Theory and Practice of Computer Science (SOFSEM 2010)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 5901))

  • 910 Accesses

Abstract

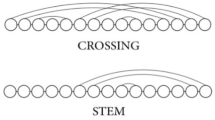
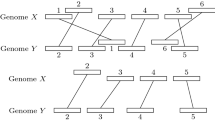
An arc-annotated string is a string of characters, called bases, augmented with a set of pairs, called arcs, each connecting two bases. Given arc-annotated strings P and Q the arc-preserving subsequence problem is to determine if P can be obtained from Q by deleting bases from Q. Whenever a base is deleted any arc with an endpoint in that base is also deleted. Arc-annotated strings where the arcs are “nested” are a natural model of RNA molecules that captures both the primary and secondary structure of these. The arc-preserving subsequence problem for nested arc-annotated strings is basic primitive for investigating the function of RNA molecules. Gramm et al. [ACM Trans. Algorithms 2006] gave an algorithm for this problem using O(nm) time and space, where m and n are the lengths of P and Q, respectively. In this paper we present a new algorithm using O(nm) time and O(n + m) space, thereby matching the previous time bound while significantly reducing the space from a quadratic term to linear. This is essential to process large RNA molecules where the space is a likely to be a bottleneck. To obtain our result we introduce several novel ideas which may be of independent interest for related problems on arc-annotated strings.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Alber, J., Gramm, J., Guo, J., Niedermeier, R.: Computing the Similarity of Two Sequences with Nested Arc Annotations. Theor. Comput. Sci. 312(2-3), 337–358 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  2. Backofen, R., Landau, G.M., Möhl, M., Tsur, D., Weimann, O.: Fast RNA Structure Alignment for Crossing Input Structures. In: Proc. 20th CPM (2009)

    Google Scholar 

  3. Bafna, V., Muthukrishnan, S., Ravi, R.: Computing Similarity between RNA Strings. In: Galil, Z., Ukkonen, E. (eds.) CPM 1995. LNCS, vol. 937, pp. 1–16. Springer, Heidelberg (1995)

    Google Scholar 

  4. Bille, P., Gørtz, I.L.: The Tree Inclusion Problem: In Optimal Space and Faster. In: Caires, L., Italiano, G.F., Monteiro, L., Palamidessi, C., Yung, M. (eds.) ICALP 2005. LNCS, vol. 3580, pp. 66–77. Springer, Heidelberg (2005)

    Google Scholar 

  5. Blin, G., Fertin, G., Rizzi, R., Vialette, S.: What Makes the Arc-Preserving Subsequence Problem Hard? In: Proc. 5th ICCS, pp. 860–868 (2005)

    Google Scholar 

  6. Blin, G., Touzet, H.: How to Compare Arc-Annotated Sequences: The Alignment Hierarchy. In: Crestani, F., Ferragina, P., Sanderson, M. (eds.) SPIRE 2006. LNCS, vol. 4209, pp. 291–303. Springer, Heidelberg (2006)

    Chapter  Google Scholar 

  7. Chen, W.: More Efficient Algorithm for Ordered Tree Inclusion. J. Algorithms 26, 370–385 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  8. Damaschke, P.: A Remark on the Subsequence Problem for Arc-Annotated Sequences with Pairwise Nested Arcs. Inf. Process. Lett. 100(2), 64–68 (2006)

    Article  MathSciNet  Google Scholar 

  9. Evans, P.: Algorithms and Complexity for Annotated Sequence Analysis. PhD Thesis, University of Victoria (1999)

    Google Scholar 

  10. Gramm, J., Guo, J., Niedermeier, R.: Pattern Matching for Arc-Annotated Sequences. ACM Trans. Algorithms 2(1), 44–65 (2006); Announced at: Agrawal, M., Seth, A.K. (eds.) FSTTCS 2002. LNCS, vol. 2556, pp. 182–193. Springer, Heidelberg (2002)

    Google Scholar 

  11. Harel, D., Tarjan, R.E.: Fast Algorithms for Finding Nearest Common Ancestors. SIAM J. Comput. 13(2), 338–355 (1984)

    Article  MATH  MathSciNet  Google Scholar 

  12. Kida, T.: Faster Pattern Matching Algorithm for Arc-Annotated Sequences. In: Jantke, K.P., Lunzer, A., Spyratos, N., Tanaka, Y. (eds.) Federation over the Web. LNCS (LNAI), vol. 3847, pp. 25–39. Springer, Heidelberg (2006)

    Chapter  Google Scholar 

  13. Kilpeläinen, P., Mannila, H.: Ordered and Unordered Tree Inclusion. SIAM J. Comput. 24, 340–356 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  14. Lin, G., Chen, Z.-Z., Jiang, T., Wen, J.: The Longest Common Subsequence Problem for Sequences with Nested Arc Annotations. J. Comput. Syst. Sci. 65(3), 465–480 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  15. Munro, I.: Tables. In: Chandru, V., Vinay, V. (eds.) FSTTCS 1996. LNCS, vol. 1180, pp. 37–42. Springer, Heidelberg (1996)

    Google Scholar 

  16. Vialette, S.: On the Computational Complexity of 2-Interval Pattern Matching Problems. Theor. Comput. Sci. 312(2-3), 223–249 (2004); Announced at CPM 2002

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Technical University of Denmark,  

    Philip Bille & Inge Li Gørtz

Authors
  1. Philip Bille
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Inge Li Gørtz
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Department of Information and Computing Sciences, Utrecht University, Padualaan 14, 3584 CH, Utrecht, The Netherlands

    Jan van Leeuwen

  2. LaBRI, Universit Bordeaux, 351 cours de la Libration, 1F-33405, Talence Cedex, France

    Anca Muscholl

  3. Department of Computer Science & Applied Mathematics, Weizmann Institute, Faculty of Mathematics and Computer Science, 76100, Rehovot, Israel

    David Peleg

  4. Department of Software Engineering Faculty of Mathematics and Physics Malostranské nám, Charles University, 25 11800, Prague 1, Czech Republic

    Jaroslav Pokorný

  5. Software Engineering, Department of Computer Science, RWTH Aachen University, 3, Ahornstrae 55, D-52074, Aachen, Germany

    Bernhard Rumpe

Rights and permissions

Reprints and permissions

Copyright information

© 2010 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Bille, P., Gørtz, I.L. (2010). Fast Arc-Annotated Subsequence Matching in Linear Space. In: van Leeuwen, J., Muscholl, A., Peleg, D., Pokorný, J., Rumpe, B. (eds) SOFSEM 2010: Theory and Practice of Computer Science. SOFSEM 2010. Lecture Notes in Computer Science, vol 5901. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-11266-9_16

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-11266-9_16

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-11265-2

  • Online ISBN: 978-3-642-11266-9

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics