Skip to main content
Springer Nature Link
Log in

Retrial Queueing Model MMAP/M 2/1 with Two Orbits

  • Conference paper
Multiple Access Communications (MACOM 2010)

Part of the book series: Lecture Notes in Computer Science ((LNCCN,volume 6235))

Included in the following conference series:

  • 646 Accesses

Abstract

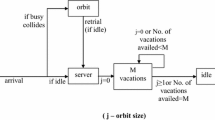
A retrial single-server queueing model with two types of customers is considered. Arrivals occur according to the Marked Markovian Arrival Process (MMAP). In case of the server occupancy at the arrival epoch, the customer moves to the orbit depending on the type of the customer. One orbit is an infinite while the second one is a a finite. Service time distributions are exponential with the parameter depending on the type of a customer. Joint distribution of the number of customers in the orbits and some performance measures are computed. Numerical results are presented. Possible extensions of the model are outlined.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Artalejo, J.R., Comez-Corral, A.: Retrial queueing systems: a computational approach. Springer, Heidelberg (2008)

    Book  MATH  Google Scholar 

  2. Domenech-Benlloch, M.J., Gimenez-Guzman, J.M., Pla, V., Casarea-Giner, V., Martinez-Bauset, J.: Solving multiserver systems with two retrial orbits using value extrapolation: a comparative perspective. In: Al-Begain, K., Fiems, D., Horváth, G. (eds.) ASMTA 2009. LNCS, vol. 5513, pp. 56–70. Springer, Heidelberg (2009)

    Chapter  Google Scholar 

  3. Dudin, S.A.: The MAP/N/N retrial queueing system with time-phased batch arrivals. Problems of Information Transmissions 45, 270–281 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  4. Gomez-Corral, A.: A bibliographical guide to the analysis of retrial queues through matrix analytic techniques. Annals of Operations Research 141, 163–191 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  5. He, Q.M.: Queues with marked customers. Advances in Applied Probability 28, 567–587 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  6. Klimenok, V.I., Dudin, A.N.: Multi-dimensional asymptotically quasi-Toeplitz Markov chains and their application in queueing theory. Queueing Systems 54, 245–259 (2006)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. INRIA Sophia Antipolis, France

    Konstantin Avrachenkov

  2. Department of Applied Mathematics and Computer Science, Belarusian State University, Minsk, 220030, Belarus

    Alexander Dudin & Valentina Klimenok

Authors
  1. Konstantin Avrachenkov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alexander Dudin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Valentina Klimenok
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Russian Academy of Sciences (SPIIRAS), Saint-Petersburg Institute for Informatics and Automation, 199178, St. Petersburg, Russia

    Alexey Vinel

  2. Department of Information and Communication Technologies, Universitat Pompeu Fabra, Roc Boronat 138, 08018, Barcelona, Spain

    Boris Bellalta  & Miquel Oliver  & 

  3. Department of Information Engineering and Computer Science (DISI), University of Trento, Via Sommarive 14, 38050, Povo (Trento), Italy

    Claudio Sacchi

  4. Institute for Information Transmission Problems, RAS, Bolshoy Karetny per., 127994, Moscow, Russia

    Andrey Lyakhov

  5. Department of Telecommunications, Budapest University of Technology and Economics, P.O. Box 91, 1521, Budapest, Hungary

    Miklós Telek

Rights and permissions

Reprints and permissions

Copyright information

© 2010 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Avrachenkov, K., Dudin, A., Klimenok, V. (2010). Retrial Queueing Model MMAP/M 2/1 with Two Orbits. In: Vinel, A., Bellalta, B., Sacchi, C., Lyakhov, A., Telek, M., Oliver, M. (eds) Multiple Access Communications. MACOM 2010. Lecture Notes in Computer Science, vol 6235. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-15428-7_12

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-15428-7_12

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-15427-0

  • Online ISBN: 978-3-642-15428-7

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics