Abstract
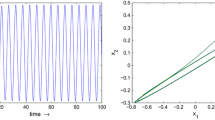
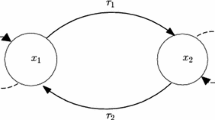
A stochastic differential equation modelling a Hopfield neural network with two neurons is investigated. Its dynamics are studied in terms of local stability analysis and Hopf bifurcation analysis. By analyzing the Lyapunov exponent, invariant measure and singular boundary theory , its nonlinear stability is investigated and Hopf bifurcations are demonstrated. The stability and direction of the Hopf bifurcation are determined from the dynamical and phenomenological points of view.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Hopfield, J.: Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA 81, 3088–3092 (1984)
Bellair, J., Campbell, S., van den Driessche, P.: Frustration, stability, and delay-induced oscillations in a neural network model. SIAM J. Appl. Math. 56, 245–255 (1996)
Cao, J., Feng, G., Wang, Y.: Multistability and multiperiodicity of delayed Cohen-Grossberg neural networks with a general class of activation functions. Physica D 237 (2008)
Wei, J., Ruan, S.: Stability and bifurcation in a neural network model with two delays. Physica D 130, 255–272 (1999)
Zou, R., Huang, L., Chen, Y.: Linear stability and Hopf bifurcation in a three-unit neural network with two delays. Neurocomputing 70, 219–228 (2006)
Song, Y., Han, M., Wei, J.: Stability and Hopf bifurcation analysis on a simplified BAM neural network with delays. Physica D 200, 185–204 (2005)
Huang, H., Daniel, W., Lam, J.: Stochastic stability analysis of fuzzy Hopfield neural networks with time-varying delays. IEEE Trans. 52, 251–265 (2005)
Haykin, S.: Neural networks. Prentice-Hall, New Jersey (1994)
Blythe, S., Mao, X., Liao, X.: Sability of stochastic delay neural networks. Journal of the Franklin Institute 338, 481–495 (2001)
Wang, Z., Lauria, S., Fang, J., Liu, X.: Exponential stability of uncertain stochastic neural networks with mixed time-delays. Chaos, Solitons and Fractals 32, 62–72 (2007)
Zhang, Y., Yue, D.: Robust delay-distribution-dependent stability of discrete-time stochastic neural networks with time-varying delay. Neurocomputing 72, 1265–1273 (2009)
Du, B., Lam, J.: Stability analysis of static recurrent neural networks using delay-partitioning and projection. Neural Networks 22, 343–347 (2009)
Wang, G., Cao, J., Wang, L.: Global dissipativity of stochastic neural networks with time delay. Journal of the Franklin Institute(2009) (accepted)
Mao, X.: Exponential Stability of Stochastic Differential Equations. Marcel Dekker, Inc., New York (1997)
Ikeda, N., Watanabe, S.: Stochastic Differential Equations and Diffusion Processes, 2nd edn. North-Holland, Amsterdam (1989)
Zhu, W.: Nonlinear Stochastic Dynamics and Control in Hamiltonian Formulation. Science Press, Beijing (2003)
Shayer, L., Campbell, S.: Stability, bifurcation and multistability in a system of two coupled neurons with multiple time delays. SIAM J. Appl. Math. 61, 673–700 (2000)
Lin, Y., Lemmert, R., Volkmann, P.: Bifurcation of periodic solution in a three-unit neural network with delay. Acta. Math. Appl. Sin. 17, 375–382 (2001)
Cao, J., Xiao, M.: Stability and Hopf Bifurcation in a Simplified BAM Neural Network With Two Time Delays. IEEE Trans. Neurl. Networks 18, 416–430 (2007)
Sun, C., Han, M.: Global Hopf bifurcation analysis on a BAM neural network with delays. Math. Comput. Modelling 45, 61–67 (2007)
Olien, L., Bellair, J.: Bifurcations, stability, and monotonicity properties of a delayed neural network model. Physica D 102, 349–363 (1997)
Potapov, A., Ali, M.: Robust chaos in neural networks. Phys. Lett. A 227, 310–322 (2000)
Liao, X., Wong, K., Wu, Z.: Bifurcation analysis in a two neuron system with continuously distributed delays. Physica D 149, 123–141 (2001)
Khasminskii, R.: On the principle of averaging for Ito’ stochastic differential equations. Kybernetika(Prague) 4, 260–279 (1968)
Lin, Y., Cai, G.: Probabilistic Structural Dynamics. Mcgraw-Hill Professional Publishing, New York (2004)
Arnold, L.: Random Dynamical Systems. Springer, New york (1998)
Namachchivaya, N.: Stochastic bifurcation. Applied Mathematics and Computation 38, 101–159 (1990)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2010 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Qin, X., Huang, Z., Tan, W. (2010). Stochastic Stability and Bifurcation Analysis on Hopfield Neural Networks with Noise. In: Li, K., Fei, M., Jia, L., Irwin, G.W. (eds) Life System Modeling and Intelligent Computing. ICSEE LSMS 2010 2010. Lecture Notes in Computer Science, vol 6329. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-15597-0_19
Download citation
DOI: https://doi.org/10.1007/978-3-642-15597-0_19
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-15596-3
Online ISBN: 978-3-642-15597-0
eBook Packages: Computer ScienceComputer Science (R0)