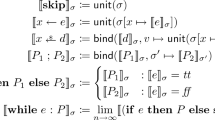Skip to main content
Springer Nature Link
Log in

Linear-Invariant Generation for Probabilistic Programs:

Automated Support for Proof-Based Methods

  • Conference paper
Static Analysis (SAS 2010)

Part of the book series: Lecture Notes in Computer Science ((LNPSE,volume 6337))

Included in the following conference series:

  • 1122 Accesses

Abstract

We present a constraint-based method for automatically generating quantitative invariants for linear probabilistic programs, and we show how it can be used, in combination with proof-based methods, to verify properties of probabilistic programs that cannot be analysed using existing automated methods. To our knowledge, this is the first automated method proposed for quantitative-invariant generation.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Probabilistic Systems Group, http://www.cse.unsw.edu.au/~carrollm/probs

  2. Bockmayr, A., Weispfenning, V.: Solving numerical constraints. In: Robinson, A., Voronkov, A. (eds.) Handbook of Automated Reasoning, vol. I, ch.12. vol. I, pp. 751–842. Elsevier Science, Amsterdam (2001)

    Chapter  Google Scholar 

  3. Celiku, O.: Mechanized Reasoning for Dually-Nondeterministic and Probabilistic Programs. PhD thesis, TUCS (2006)

    Google Scholar 

  4. Ciesinski, F., Baier, C.: LiQuor: A tool for qualitative and quantitative linear time analysis of reactive systems. In: Quantitative Evaluation of Systems (QEST), pp. 131–132. IEEE Computer Society Press, Los Alamitos (2006)

    Google Scholar 

  5. Colón, M., Sankaranarayanan, S., Sipma, H.: Linear invariant generation using non-linear constraint solving. In: Hunt Jr., W.A., Somenzi, F. (eds.) CAV 2003. LNCS, vol. 2725, pp. 420–432. Springer, Heidelberg (2003)

    Chapter  Google Scholar 

  6. Cousot, P.: Proving program invariance and termination by parametric abstraction, Lagrangian relaxation and semidefinite programming. In: Cousot, R. (ed.) VMCAI 2005. LNCS, vol. 3385, pp. 1–24. Springer, Heidelberg (2005)

    Google Scholar 

  7. Cousot, P., Cousot, R.: Abstract interpretation: A unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: Principles of Programming Languages (PoPL), pp. 238–252. ACM, New York (1977)

    Google Scholar 

  8. den Hartog, J., de Vink, E.P.: Verifying probabilistic programs using a Hoare like logic. Int. J. Found. Comput. Sci. 13(3), 315–340 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  9. Di Pierro, A., Wiklicky, H.: Concurrent constraint programming: towards probabilistic abstract interpretation. In: Gabbrielli, M., Pfenning, F. (eds.) Principles and Practice of Declarative Programming (PPDP), pp. 127–138. ACM, New York (2000)

    Google Scholar 

  10. Di Pierro, A., Wiklicky, H.: Measuring the precision of abstract interpretations. In: Lau, K. (ed.) LOPSTR 2000. LNCS, vol. 2042, pp. 147–164. Springer, Heidelberg (2001)

    Chapter  Google Scholar 

  11. Dijkstra, E.W.: A Discipline of Programming. Prentice-Hall, Englewood Cliffs (1976)

    MATH  Google Scholar 

  12. Dolzmann, A., Sturm, T.: REDLOG: computer algebra meets computer logic. SIGSAM Bull. 31(2), 2–9 (1997)

    Article  MathSciNet  Google Scholar 

  13. Floyd, R.W.: Assigning meanings to programs. In: Schwartz, J.T. (ed.) Mathematical Aspects of Computer Science. Proc. Symp. Appl. Math., vol. 19, pp. 19–32. American Mathematical Society, Providence (1967)

    Google Scholar 

  14. Gulwani, S., Srivastava, S., Venkatesan, R.: Program analysis as constraint solving. Programming Language Design and Implementation (PLDI) 43(6), 281–292 (2008)

    Google Scholar 

  15. Hazewinkel, M.: Encyclopedia of Mathematics. Springer, Heidelberg (2002)

    Google Scholar 

  16. Hermanns, H., Wachter, B., Zhang, L.: Probabilistic CEGAR. In: Gupta, A., Malik, S. (eds.) CAV 2008. LNCS, vol. 5123, pp. 162–175. Springer, Heidelberg (2008)

    Chapter  Google Scholar 

  17. Hinton, A., Kwiatkowska, M., Norman, G., Parker, D.: PRISM: A tool for automatic verification of probabilistic systems. In: Hermanns, H., Palsberg, J. (eds.) TACAS 2006. LNCS, vol. 3920, pp. 441–444. Springer, Heidelberg (2006)

    Chapter  Google Scholar 

  18. Hoare, C.A.R.: An axiomatic basis for computer programming. Communications of the ACM 12(10), 576–580 (1969)

    Article  MATH  Google Scholar 

  19. Hurd, J.: Formal Verification of Probabilistic Algorithms. PhD thesis, University of Cambridge (2002)

    Google Scholar 

  20. Hurd, J., McIver, A.K., Morgan, C.C.: Probabilistic guarded commands mechanised in HOL. Theoretical Computer Science 346(1), 96–112 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  21. Kapur, D.: Automatically generating loop invariants using quantifier elimination. In: Deduction and Applications (2005)

    Google Scholar 

  22. Katoen, J.P., McIver, A.K., Meinicke, L.A., Morgan, C.C.: Linear-invariant generation for probabilistic programs: automated support for proof-based methods. Draft of this paper including its appendices [1, Katoen:10] (2010)

    Google Scholar 

  23. Kattenbelt, M.: Private communication (2010)

    Google Scholar 

  24. Kattenbelt, M., Kwiatkowska, M., Norman, G., Parker, D.: Abstraction refinement for probabilistic software. In: Jones, N.D., Müller-Olm, M. (eds.) VMCAI 2009. LNCS, vol. 5403, pp. 182–197. Springer, Heidelberg (2009)

    Chapter  Google Scholar 

  25. Kozen, D.: Semantics of probabilistic programs. Jnl. Comp. Sys. Sciences 22, 328–350 (1981)

    Article  MATH  MathSciNet  Google Scholar 

  26. Legay, A., Murawski, A.S., Ouaknine, J., Worrell, J.: On automated verification of probabilistic programs. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 173–187. Springer, Heidelberg (2008)

    Chapter  Google Scholar 

  27. McIver, A.K., Morgan, C.C.: Abstraction, Refinement and Proof for Probabilistic Systems. Monographs in Computer Science. Springer, Heidelberg (2004)

    Google Scholar 

  28. Monniaux, D.: Abstract interpretation of probabilistic semantics. In: Palsberg, J. (ed.) SAS 2000. LNCS, vol. 1824, pp. 322–339. Springer, Heidelberg (2000)

    Google Scholar 

  29. Morgan, C.C.: Proof rules for probabilistic loops. In: Jifeng, H., Cooke, J., Wallis, P. (eds.) BCS-FACS 7th Refinement Workshop, Workshops in Computing. Springer, Heidelberg (1996)

    Google Scholar 

  30. Podelski, A., Rybalchenko, A.: A complete method for the synthesis of linear ranking functions. In: Steffen, B., Levi, G. (eds.) VMCAI 2004. LNCS, vol. 2937, pp. 239–251. Springer, Heidelberg (2004)

    Chapter  Google Scholar 

  31. Sankaranarayanan, S., Sipma, H.B., Manna, Z.: Non-linear loop invariant generation using Gröbner bases. In: Principles of Programming Languages (PoPL), pp. 318–329. ACM, New York (2004)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Software Modeling and Verification Group, RWTH Aachen University, Germany

    Joost-Pieter Katoen

  2. Dept. Computer Science, Macquarie University, NSW 2109, Australia

    Annabelle K. McIver & Larissa A. Meinicke

  3. School of Comp. Sci. and Eng., Univ. New South Wales, NSW 2052, Australia

    Carroll C. Morgan

Authors
  1. Joost-Pieter Katoen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Annabelle K. McIver
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Larissa A. Meinicke
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Carroll C. Morgan
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Départment d’Informatique, École normale supérieure, rue d’Ulm 45, 75230, Paris cedex, France

    Radhia Cousot

  2. ELIAUS-DALI Laboratory, Université de Perpignan Via Domitia, 52, avenue Paul Alduy, 66860, Perpignan cedex, France

    Matthieu Martel

Rights and permissions

Reprints and permissions

Copyright information

© 2010 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Katoen, JP., McIver, A.K., Meinicke, L.A., Morgan, C.C. (2010). Linear-Invariant Generation for Probabilistic Programs: . In: Cousot, R., Martel, M. (eds) Static Analysis. SAS 2010. Lecture Notes in Computer Science, vol 6337. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-15769-1_24

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-15769-1_24

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-15768-4

  • Online ISBN: 978-3-642-15769-1

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics