Abstract
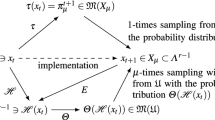
In the paper we consider the ranking given by the Pareto dominance relation as a basis to create a selection operator for the Evolutionary Multiobjective Optimization Algorithm (EMOA). Assuming that sampling to the next epoch is performed according to the generalized Bernoulli schema with regard to a selected type of the rank selection, a heuristic operator for EMOA is introduced. Having defined the heuristic operator, the transition probability matrix of the uniform Markov chain modeling EMOA can be explicitly obtained as in the Vose’s theory of the Simple Genetic Algorithm (SGA). This chain is ergodic if the mixing operator following the EMOA selection operator in each epoch is strictly positive. Moreover, we show that the measure on the space of populations imposed by the EMOA infinite population concentrates on the set of fixed points of the heuristic operator after infinite number of epochs, assuming that the heuristic operator is focusing.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Billingsley, P.: Probability and Measure. John Wiley and Sons, Chichester (1979)
Coello Coello, C.A., Lamont, G.B.: Applications of Multi-objective Evolutionary Algorithms. World Scientific, Singapore (2004)
Emmerich, M., Beume, N., Naujoks, B.: An EMO algorithm using the hypervolume measure as selection criterion. In: Coello Coello, C.A., Hernández Aguirre, A., Zitzler, E. (eds.) EMO 2005. LNCS, vol. 3410, pp. 62–76. Springer, Heidelberg (2005)
Fonseca, C.M., Fleming, P.J.: Genetic algorithms for multiobjective optimization: Formulation, discussion and generalization. In: Genetic Algorithms: Proceedings of the Fifth International Conference, pp. 416–423 (1993)
Goldberg, D.E.: Genetic Algorithms in Search, Optimization and Machine Learnings. Addison-Wesley, Reading (1989)
Hanne, T.: On the convergence of multiobjective evolutionary algorithms. European Journal of Operational Research 117(3), 553–564 (1999)
Laumanns, M.: Stochastic convergence of random search to fixed size Pareto set approximations (2007)
Nix, A.E., Vose, M.D.: Modelling genetic algorithms with Markov chains. Annals of Mathematics and Artificial Intelligence 5, 79–88 (1992)
Rudolph, G.: On a multi-objective evolutionary algorithm and its convergence to the Pareto set. In: Proceedings of the 5th IEEE Conference on Evolutionary Computation, pp. 511–516. IEEE Press, Los Alamitos (1998)
Rudolph, G., Agapie, A.: Convergence properties of some multi-objective evolutionary algorithms. In: Congress on Evolutionary Computation (CEC 2000), pp. 1010–1016. IEEE Press, Los Alamitos (2000)
Schaefer, R., Telega, H.: Foundation of Global Genetic Optimization. Springer, Heidelberg (2007)
Srinivas, N., Deb, K.: Multiobjective optimization using nondominated sorting in genetic algorithms. Evolutionary Computation (1994)
Vose, M.D.: The Simple Genetic Algorithm. MIT Press, Cambridge (1999)
Zitzler, E.: Evolutionary Algorithms for Multiobjective Optimization: Methods and Applications. PhD thesis, ETH Zurich, Switzerland (1999)
Zitzler, E., Laumanns, M., Thiele, L.: SPEA2: Improving the Strength Pareto Evolutionary Algorithm for Multiobjective Optimization. In: Evolutionary Methods for Design, Optimisation and Control with Application to Industrial Problems (EUROGEN 2001), pp. 95–100. International Center for Numerical Methods in Engineering, CIMNE (2002)
Zitzler, E., Thiele, L.: Multiobjective evolutionary algorithms: A comparative case study and the strength pareto evolutionary algorithm. IEEE Transactions on Evolutionary Computation 3(4), 257–271 (1999)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2010 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Gajda, E., Schaefer, R., Smołka, M. (2010). Evolutionary Multiobjective Optimization Algorithm as a Markov System. In: Schaefer, R., Cotta, C., Kołodziej, J., Rudolph, G. (eds) Parallel Problem Solving from Nature, PPSN XI. PPSN 2010. Lecture Notes in Computer Science, vol 6238. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-15844-5_62
Download citation
DOI: https://doi.org/10.1007/978-3-642-15844-5_62
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-15843-8
Online ISBN: 978-3-642-15844-5
eBook Packages: Computer ScienceComputer Science (R0)