Abstract
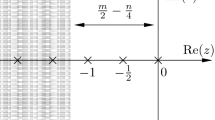
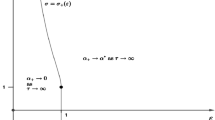
The nonlinear elliptic problem considered arises when investigating a class of self-similar solutions of a reaction-diffusion equation. We focus our study on the solutions of spiral structure. The proposed approach is based on the continuous analog of the Newton’s method and on the Galerkin finite element method. To reveal solutions of spiral structure appropriate initial approximations are used. The last ones are expressed by the confluent hypergeometric function 1 F 1(a,b;z). Algorithms for accurate, fast and reliable computation of its values for broad ranges of the parameters a and b and of the variable z are worked out. A detailed numerical analysis of the evolution of the spiral structure solutions with respect to the medium parameters, including critical values, is carried out.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Abramovitz, M., Stegun, I.A. (eds.): Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards (1970)
Akhromeeva, T.S., Kurdyumov, S.P., Malinetskii, G.G., Samarskii, A.A.: Chaos and Dissipative Structures in Reaction-Diffusion Systems. Nauka, Moscow (1992)
Dimova, S.N., Kastchiev, M.S., Koleva, M.G., Vasileva, D.P.: Numerical Analysis of Radially Nonsymmetric Blow-up Solutions of a Nonlinear Parabolic Problem. J. Comp. Appl. Math. 97, 81–97 (1998)
Dimova, S.N., Vasileva, D.P.: Numerical Realization of Blow-up Spiral Wave Solutions of a Nonlinear Heat-Transfer Equation. Int. J. Num. Meth. Heat Fluid Flow 4, 497–511 (1994)
Galaktionov, V.A., Dorodnicyn, V.A., Elenin, G.G., Kurdyumov, S.P., Samarskii, A.A.: The Quasilinear Heat Conduction Equation with a Source: Enhanesment, Localization, Symmetry, Exact Solutions, Asymptotic Forms and Structures. J. Sov. Math (JOSMAR) 41, 1163–1356 (1988)
Gil, A., Segura, J., Temme, N.M.: Numerical Methods for Special Functions. SIAM, Philadelphia (2007)
Koleva, M.G., Dimova, S.N., Kaschiev, M.S.: Analisys of the Eigen Functions of Combustion of a Nonlinear Medium in Polar Coordinates. Math. Modeling 3, 76–83 (1992)
Kurkina, E.S., Nikol’ski, I.M.: Bifurcation Analysis of the Spectrum of Two-Dimentional Thermal Structures Evolving with Blow-up. Comp. Math. and Modeling 17(4), 320–340 (2006)
Kurdyumov, S.P., Kurkina, E.S., Potapov, A.B., Samarskii, A.A.: Complex Multidimensional Structures of Combustion of a Nonlinear Medium. Dokl. Acad. Nauk SSSR 274, 1071–1075 (1984)
Luke, Y.: Algorithms for the Computation of Mathematical Functions. Academic Press, London (1977)
Puzynin, I.V., et al.: Methods of Computational Physics for Investigation of Models of Complex Physical Systems. Particals & Nucley 38 (2007)
Samarskii, A.A., Galaktionov, V.A., Kurdyumov, S.P., Mikhailov, A.P.: Blowup in Problems for Quasilinear Parabolic Equations. Walter de Gruyter, Berlin (1988)
Zhang, S., Jin, J.: Computation of Special Functions. John Wiley & Sons, Chichester (1996)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Dimova, M., Dimova, S. (2011). Numerical Investigation of Spiral Structure Solutions of a Nonlinear Elliptic Problem. In: Dimov, I., Dimova, S., Kolkovska, N. (eds) Numerical Methods and Applications. NMA 2010. Lecture Notes in Computer Science, vol 6046. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-18466-6_47
Download citation
DOI: https://doi.org/10.1007/978-3-642-18466-6_47
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-18465-9
Online ISBN: 978-3-642-18466-6
eBook Packages: Computer ScienceComputer Science (R0)