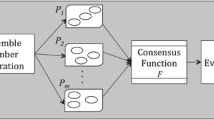
Abstract
Various approaches to produce cluster ensembles and several consensus functions to combine data partitions have been proposed in order to obtain a more robust partition of the data. However, the existence of many approaches leads to another problem which consists in knowing which of these approaches to produce the cluster ensembles’ data and to combine these partitions best fits a given data set. In this paper, we propose a new measure to select the best consensus data partition, among a variety of consensus partitions, based on the concept of average cluster consistency between each data partition that belongs to the cluster ensemble and a given consensus partition. The experimental results obtained by comparing this measure with other measures for cluster ensemble selection in 9 data sets, showed that the partitions selected by our measure generally were of superior quality in comparison with the consensus partitions selected by other measures.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Fred, A.L.N.: Finding consistent clusters in data partitions. In: Kittler, J., Roli, F. (eds.) MCS 2001. LNCS, vol. 2096, pp. 309–318. Springer, Heidelberg (2001)
Strehl, A., Ghosh, J.: Cluster ensembles — a knowledge reuse framework for combining multiple partitions. J. Mach. Learn. Res. 3, 583–617 (2003)
Fred, A.L.N., Jain, A.K.: Combining multiple clusterings using evidence accumulation. IEEE Trans. Pattern Anal. Mach. Intell. 27(6), 835–850 (2005)
Duarte, F.J., Fred, A.L.N., Rodrigues, M.F.C., Duarte, J.: Weighted evidence accumulation clustering using subsampling. In: Sixth International Workshop on Pattern Recognition in Information Systems (2006)
Fern, X., Brodley, C.: Solving cluster ensemble problems by bipartite graph partitioning. In: ICML 2004: Proceedings of the Twenty-First International Conference on Machine Learning, vol. 36. ACM, New York (2004)
Topchy, A.P., Jain, A.K., Punch, W.F.: A mixture model for clustering ensembles. In: Berry, M.W., Dayal, U., Kamath, C., Skillicorn, D.B. (eds.) SDM. SIAM, Philadelphia (2004)
Jouve, P., Nicoloyannis, N.: A new method for combining partitions, applications for distributed clustering. In: International Workshop on Paralell and Distributed Machine Learning and Data Mining (ECML/PKDD 2003), pp. 35–46 (2003)
Topchy, A., Minaei-Bidgoli, B., Jain, A.K., Punch, W.F.: Adaptive clustering ensembles. In: ICPR 2004: Proceedings of the Pattern Recognition, 17th International Conference on (ICPR 2004), vol. 1, pp. 272–275. IEEE Computer Society, Los Alamitos (2004)
Topchy, A., Jain, A.K., Punch, W.: Combining multiple weak clusterings, pp. 331–338 (2003)
Hadjitodorov, S.T., Kuncheva, L.I., Todorova, L.P.: Moderate diversity for better cluster ensembles. Inf. Fusion 7(3), 264–275 (2006)
Hubert, L., Arabie, P.: Comparing partitions. Journal of Classification (October 1985)
Kuncheva, L., Hadjitodorov, S.: Using diversity in cluster ensembles, vol. 2, pp. 1214–1219 (October 2004)
Duarte, F., Duarte, J., Fred, A., Rodrigues, F.: Cluster ensemble selection - using average cluster consistency. In: International Conference on Discovery and Information Retrieval (KDIR 2009), Funchal, October 6-8, pp. 85–95 (2009)
Sneath, P., Sokal, R.: Numerical taxonomy. Freeman, London (1973)
King, B.: Step-wise clustering procedures. Journal of the American Statistical Association (69), 86–101 (1973)
Macqueen, J.B.: Some methods of classification and analysis of multivariate observations. In: Proceedings of the Fifth Berkeley Symposium on Mathemtical Statistics and Probability, pp. 281–297 (1967)
Ng, R.T., Han, J.: Clarans: A method for clustering objects for spatial data mining. IEEE Trans. on Knowl. and Data Eng. 14(5), 1003–1016 (2002)
Karypis, G., Han, E., News, V.K.: Chameleon: Hierarchical clustering using dynamic modeling. Computer 32(8), 68–75 (1999)
Agrawal, R., Gehrke, J., Gunopulos, D., Raghavan, P.: Automatic subspace clustering of high dimensional data for data mining applications. SIGMOD Rec. 27(2), 94–105 (1998)
Guha, S., Rastogi, R., Shim, K.: Cure: an efficient clustering algorithm for large databases. In: SIGMOD 1998: Proceedings of the 1998 ACM SIGMOD International Conference on Management of Data, pp. 73–84. ACM, New York (1998)
Ester, M., Kriegel, H.P., Jörg, S., Xu, X.: A density-based algorithm for discovering clusters in large spatial databases with noise (1996)
Wang, W., Yang, J., Muntz, R.R.: Sting: A statistical information grid approach to spatial data mining. In: VLDB 1997: Proceedings of the 23rd International Conference on Very Large Data Bases, pp. 186–195. Morgan Kaufmann Publishers Inc., San Francisco (1997)
Ward, J.H.: Hierarchical grouping to optimize an objective function. Journal of the American Statistical Association 58(301), 236–244 (1963)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Duarte, F.J.F., Duarte, J.M.M., Fred, A.L.N., Rodrigues, M.F.C. (2011). Average Cluster Consistency for Cluster Ensemble Selection. In: Fred, A., Dietz, J.L.G., Liu, K., Filipe, J. (eds) Knowledge Discovery, Knowlege Engineering and Knowledge Management. IC3K 2009. Communications in Computer and Information Science, vol 128. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-19032-2_10
Download citation
DOI: https://doi.org/10.1007/978-3-642-19032-2_10
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-19031-5
Online ISBN: 978-3-642-19032-2
eBook Packages: Computer ScienceComputer Science (R0)