Abstract
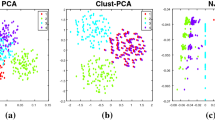
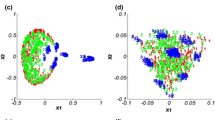
We address in this paper the problem of finding low-dimensional representation spaces for clustered high-dimensional data. The new embedding space proposed here, called the cluster space, is an unsupervised dimension reduction method that relies on the estimation of a Gaussian Mixture Model (GMM) parameters. This allows to capture information not only among data points, but also among clusters in the same embedding space. Points are represented in the cluster space by means of their a posteriori probability values estimated using the GMMs. We show the relationship between the cluster space and the Quadratic Discriminant Analysis (QDA), thus emphasizing the discriminant capability of the representation space proposed. The estimation of the parameters of the GMM in high dimensions is further discussed. Experiments on both artificial and real data illustrate the discriminative power of the cluster space compared with other known state-of-the-art embedding methods.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Belkin, M., Niyogi, P.: Laplacian eigenmaps and spectral techniques for embedding and clustering. In: Advances in Neural Information Processing Systems, vol. 14 (2002)
Borg, I., Groenen, P.: Modern multidimensional scaling: Theory and applications. Springer, Heidelberg (2005)
Demartines, P., Hérault, J.: Curvilinear component analysis: A self-organizing neural network for nonlinear mapping of data sets. IEEE Transactions on Neural Network (1997)
Dempster, A.P., Laird, N.M., Rubin, D.B.: Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society 39 (1977)
Fraley, C., Raftery, A.: Model-based clustering, discriminant analysis and density estimation. Journal of American Statistical Association, 611–631 (2002)
Gupta, G., Ghosh, J.: Detecting seasonal trends and cluster motion visualization for very high-dimensional transactional data. In: Proceedings of the First International SIAM Conference on Data Mining (2001)
Hastie, T., Tibshirani, R., Friedman, J.: The elements of statistical learning. Springer, Heidelberg (2001)
Hinton, G., Roweis, S.: Stochastic neighbor embedding. In: Advances in Neural Information Processing Systems (2002)
Iwata, T., Saito, K., Ueda, N., Stromsten, S., Griffiths, T., Tenenbaum, J.: Parametric embedding for class visualization. Neural Computation (2007)
Iwata, T., Yamada, T., Ueda, N.: Probabilistic latent semantic visualization: topic model for visualizing documents. In: Proceedings of the 14th ACM SIGKDD, USA, pp. 363–371 (2008)
Kriegel, H.-P., Kroger, P., Zimek, A.: Clustering high-dimensional data: A survey on subspace clustering, pattern-based clustering and correlation clustering. ACM Transactions on Knowledge Discovery from Data (TKDD) 3 (2009)
Lee, J., Lendasse, A., Verleysen, M.: A robust nonlinear projection method. In: Proceedings of ESANN 2000, Belgium, pp. 13–20 (2000)
MacQueen, J.B.: Some Methods for Classification and Analysis of MultiVariate Observations. In: Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, vol. 1, pp. 281–297 (1967)
Roweis, S., Saul, L.: Nonlinear dimensionality reduction by locally linear embedding. Science 290, 2323–2326 (2000)
Sammon, J.W.: A nonlinear mapping for data structure analysis. IEEE Transactions on Computers C-18 (1969)
Tenenbaum, J., de Silva, V., Langford, J.: A global geometric framework for nonlinear dimensionality reduction. Science 290, 2319–2323 (2000)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Szekely, E., Bruno, E., Marchand-Maillet, S. (2011). Unsupervised Quadratic Discriminant Embeddings Using Gaussian Mixture Models. In: Fred, A., Dietz, J.L.G., Liu, K., Filipe, J. (eds) Knowledge Discovery, Knowlege Engineering and Knowledge Management. IC3K 2009. Communications in Computer and Information Science, vol 128. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-19032-2_8
Download citation
DOI: https://doi.org/10.1007/978-3-642-19032-2_8
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-19031-5
Online ISBN: 978-3-642-19032-2
eBook Packages: Computer ScienceComputer Science (R0)