Abstract
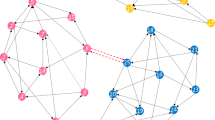
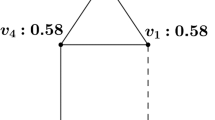
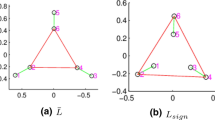
Previous studies on social networks are often focused on networks with only positive relations between individual nodes. As a significant extension, we conduct the spectral analysis on graphs with both positive and negative edges. Specifically, we investigate the impacts of introducing negative edges and examine patterns in the spectral space of the graph’s adjacency matrix. Our theoretical results show that communities in a k-balanced signed graph are distinguishable in the spectral space of its signed adjacency matrix even if connections between communities are dense. This is quite different from recent findings on unsigned graphs, where communities tend to mix together in the spectral space when connections between communities increase. We further conduct theoretical studies based on graph perturbation to examine spectral patterns of general unbalanced signed graphs. We illustrate our theoretical findings with various empirical evaluations.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Bansal, N., Chawla, S.: Correlation clustering. Machine Learning 56, 238–247 (2002)
Davis, J.A.: Clustering and structural balance in graphs. Human Relations 20, 181–187 (1967)
Demaine, E.D., Immorlica, N.: Correlation clustering with partial information. In: Working Notes of the 6th International Workshop on Approximation Algorithms for Combinatorial Optimization Problems, pp. 1–13 (2003)
Hage, P., Harary, F.: Structural models in anthropology, pp. 56–60. Cambridge University Press, Cambridge (1983)
Inohara, T.: Characterization of clusterability of signed graph in terms of newcomb’s balance of sentiments. Applied Mathematics and Computation 133, 93–104 (2002)
Kunegis, J., Lommatzsch, A., Bauckhage, C.: The slashdot zoo: mining a social network with negative edges. In: WWW 2009, pp. 741–750 (2009)
Kunegis, J., Schmidt, S., Lommatzsch, A., Lerner, J., Luca, E.W.D., Albayrak, S.: Spectral analysis of signed graphs for clustering, prediction and visualization. In: SDM, pp. 559–570 (2010)
Leskovec, J., Huttenlocher, D., Kleinberg, J.: Signed networks in social media. In: CHI, pp. 1361–1370 (2010)
Prakash, B.A., Sridharan, A., Seshadri, M., Machiraju, S., Faloutsos, C.: EigenSpokes: Surprising patterns and scalable community chipping in large graphs. In: Zaki, M.J., Yu, J.X., Ravindran, B., Pudi, V. (eds.) PAKDD 2010. LNCS, vol. 6119, pp. 435–448. Springer, Heidelberg (2010)
Stewart, G.W., Sun, J.: Matrix perturbation theory. Academic Press, London (1990)
Wu, L., Ying, X., Wu, X., Zhou, Z.-H.: Line orthogonality in adjacency eigenspace and with application to community partition. Technical Report, UNC Charlotte (2010)
Ying, X., Wu, X.: On randomness measures for social networks. In: SDM, pp. 709–720 (2009)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Wu, L., Ying, X., Wu, X., Lu, A., Zhou, ZH. (2011). Spectral Analysis of k-Balanced Signed Graphs. In: Huang, J.Z., Cao, L., Srivastava, J. (eds) Advances in Knowledge Discovery and Data Mining. PAKDD 2011. Lecture Notes in Computer Science(), vol 6635. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-20847-8_1
Download citation
DOI: https://doi.org/10.1007/978-3-642-20847-8_1
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-20846-1
Online ISBN: 978-3-642-20847-8
eBook Packages: Computer ScienceComputer Science (R0)