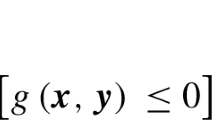Skip to main content
Springer Nature Link
Log in

Branch-and-Bound Reduction Type Method for Semi-Infinite Programming

  • Conference paper
Computational Science and Its Applications - ICCSA 2011 (ICCSA 2011)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 6784))

Included in the following conference series:

  • 1394 Accesses

Abstract

Semi-infinite programming (SIP) problems can be efficiently solved by reduction type methods. Here, we present a new reduction method for SIP, where the multi-local optimization is carried out with a multi-local branch-and-bound method, the reduced (finite) problem is approximately solved by an interior point method, and the global convergence is promoted through a two-dimensional filter line search. Numerical experiments with a set of well-known problems are shown.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. El-Bakry, A.S., Tapia, R.A., Tsuchiya, T., Zhang, Y.: On the formulation and theory of the Newton interior-point method for nonlinear programming. Journal of Optimization Theory and Applications 89, 507–541 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  2. Ben-Tal, A., Teboule, M., Zowe, J.: Second order necessary optimality conditions for semi-infinite programming problems. Lecture Notes in Control and Information Sciences, vol. 15, pp. 17–30 (1979)

    Google Scholar 

  3. Coope, I.D., Watson, G.: A projected Lagrangian algorithm for semi-infinite programming. Mathematical Programming 32, 337–356 (1985)

    Article  MATH  MathSciNet  Google Scholar 

  4. Fletcher, R., Leyffer, S.: Nonlinear programming without a penalty function. Mathematical Programming 91, 239–269 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  5. Goberna, M.A., López, M.A. (eds.): Semi-Infinite Programming. Recent Advances in Nonconvex Optimization and Its Applications. Springer, Heidelberg (2001)

    MATH  Google Scholar 

  6. Hendrix, E.M.T., G-Tóth, B.: Introduction to nonlinear and global optimization. Springer optimization and its applications, vol. 37. Springer, Heidelberg (2010)

    MATH  Google Scholar 

  7. Hettich, R., Jongen, H.T.: Semi-infinite programming: conditions of optimality and applications. In: Stoer, J. (ed.) Lectures Notes in Control and Information Science - Optimization Techniques, vol. 7, pp. 1–11. Springer, Heidelberg (1978)

    Google Scholar 

  8. Hettich, R., Kortanek, K.O.: Semi-infinite programming: Theory, methods and applications. SIAM Review 35, 380–429 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  9. Horst, R., Tuy, H.: Global optimization. deterministic approaches. Springer, Heidelberg (1996)

    Book  MATH  Google Scholar 

  10. Ingber, L.: Very fast simulated re-annealing. Mathematical and Computer Modelling 12, 967–973 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  11. Li, D.-H., Qi, L., Tam, J., Wu, S.-Y.: A smoothing Newton method for semi-infinite programming. Journal of Global Optimization 30, 169–194 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  12. Ling, C., Ni, Q., Qi, L., Wu, S.-Y.: A new smoothing Newton-type algorithm for semi-infinite programming. Journal of Global Optimization 47, 133–159 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  13. Liu, G.-x.: A homotopy interior point method for semi-infinite programming problems. Journal of Global Optimization 37, 631–646 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  14. López, M., Still, G.: Semi-infinite programming. European Journal of Operations Research 180, 491–518 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  15. Nocedal, J., Wright, S.J.: Numerical Optimization. Springer, Heidelberg (1999)

    Book  MATH  Google Scholar 

  16. Parsopoulos, K., Plagianakos, V., Magoulas, G., Vrahatis, M.: Objective function stretching to alleviate convergence to local minima. Nonlinear Analysis 47, 3419–3424 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  17. Pereira, A.I.P.N., Fernandes, E.M.G.P.: On a reduction line search filter method for nonlinear semi-infinite programming problems. In: Sakalauskas, L., Weber, G.W., Zavadskas, E.K. (eds.) Euro Mini Conference Continuous Optimization and Knowledge-Based Technologies, vol. 9, pp. 174–179 (2008), ISBN: 978-9955-28-283-9

    Google Scholar 

  18. Pereira, A.I.P.N., Fernandes, E.M.G.P.: An Hyperbolic Penalty Filter Method for Semi-Infinite Programming. Numerical Analysis and Applied Mathematics. In: Simos, T.E., Psihoyios, G., Tsitouras, C. (eds.) AIP Conference Proceedings, vol. 1048, pp. 269–273. Springer, Heidelberg (2008)

    Google Scholar 

  19. Pereira, A.I.P.N., Fernandes, E.M.G.P.: A reduction method for semi-infinite programming by means of a global stochastic approach. Optimization 58, 713–726 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  20. Price, C.J., Coope, I.D.: Numerical experiments in semi-infinite programming. Computational Optimization and Applications 6, 169–189 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  21. Qi, L., Wu, W.S.-Y., Zhou, G.: Semismooth Newton methods for solving semi-infinite programming problems. Journal of Global Optimization 27, 215–232 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  22. Qi, L., Ling, C., Tong, X., Zhou, G.: A smoothing projected Newton-type algorithm for semi-infinite programming. Computational Optimization and Applications 42, 1–30 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  23. Reemtsen, R., Rückmann, J.-J.: Semi-infinite programming. Nonconvex Optimization and Its Applications, vol. 25. Kluwer Academic Publishers, Dordrecht (1998)

    MATH  Google Scholar 

  24. Shanno, D.F., Vanderbei, R.J.: Interior-point methods for nonconvex nonlinear programming: orderings and higher-order methods, Mathematical Programming Ser. B 87, 303–316 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  25. Silva, R., Ulbrich, M., Ulbrich, S., Vicente, L.N.: A globally convergent primal-dual interior-point filter method for nonlinear programming: new filter optimality measures and computational results, preprint 08-49, Dept. Mathematics, U. Coimbra (2008)

    Google Scholar 

  26. Stein, O., Still, G.: Solving semi-infinite optimization problems with interior point techniques. SIAM Journal on Control and Optimization 42, 769–788 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  27. Tanaka, Y., Fukushima, M., Ibaraki, T.: A comparative study of several semi-infinite nonlinear programmnig algorithms. European Journal of Operations Research 36, 92–100 (1988)

    Article  MATH  Google Scholar 

  28. Ulbrich, M., Ulbrich, S., Vicente, L.N.: A globally convergent primal-dual interior-point filter method for nonlinear programming. Mathematical Programming 100, 379–410 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  29. Vanderbei, R.J., Shanno, D.F.: An interior-point algorithm for nonconvex nonlinear programming. Computational Optimization and Applications 13, 231–252 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  30. Vaz, A.I.F., Fernandes, E.M.G.P., Gomes, M.P.S.F.: Robot trajectory planning with semi-infinite programming. European Journal of Operational Research 153, 607–617 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  31. Vaz, A.I.F., Ferreira, E.C.: Air pollution control with semi-infinite programming. Applied Mathematical Modelling 33, 1957–1969 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  32. Vázquez, F.G., Rückmann, J.-J., Stein, O., Still, G.: Generalized semi-infinite programming: a tutorial. Journal of Computational and Applied Mathematics 217, 394–419 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  33. Wächter, A., Biegler, L.T.: Line search filter methods for nonlinear programming: motivation and global convergence. SIAM Journal on Optimization 16, 1–31 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  34. Wächter, A., Biegler, L.T.: Line search filter methods for nonlinear programming: local convergence. SIAM Journal on Optimization 16, 32–48 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  35. Wächter, A., Biegler, L.T.: On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Mathematical Programming 106, 25–57 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  36. Weber, G.-W., Tezel, A.: On generalized semi-infinite optimization of genetic network. TOP 15, 65–77 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  37. Yi-gui, O.: A filter trust region method for solving semi-infinite programming problems. Journal of Applied Mathematics and Computing 29, 311–324 (2009)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Polytechnic Institute of Bragança, ESTiG-Gab 54, 5301-857, Bragança, Portugal

    Ana I. Pereira

  2. Algoritmi R&D Centre, University of Minho, Campus de Gualtar, 4710-057, Braga, Portugal

    Edite M. G. P. Fernandes

Authors
  1. Ana I. Pereira
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Edite M. G. P. Fernandes
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. L.I.S.U.T. - D.A.P.I.T., Basilicata University Potenza, 10, Viale dell’Ateneo Lucano, 85100, Potenza, Italy

    Beniamino Murgante

  2. Department of Mathematics and Computer Science, University of Perugia, Via Vanvitelli, 1, 06123, Perugia, Italy

    Osvaldo Gervasi

  3. Department of Applied Mathematics and Computational Sciences, University of Cantabria, Avda. de los Castros, s/n, C.P. 39005, Santander, Spain

    Andrés Iglesias

  4. School of Business Systems, Monash University, 3800, Clayton, VIC, Australia

    David Taniar

  5. Department of Intelligent Informatics, Kyushu Sangyo University, 2-3-1 Matsukadai, Higashi-ku, 813-8503, Fukuoka, Japan

    Bernady O. Apduhan

Rights and permissions

Reprints and permissions

Copyright information

© 2011 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Pereira, A.I., Fernandes, E.M.G.P. (2011). Branch-and-Bound Reduction Type Method for Semi-Infinite Programming. In: Murgante, B., Gervasi, O., Iglesias, A., Taniar, D., Apduhan, B.O. (eds) Computational Science and Its Applications - ICCSA 2011. ICCSA 2011. Lecture Notes in Computer Science, vol 6784. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-21931-3_23

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-21931-3_23

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-21930-6

  • Online ISBN: 978-3-642-21931-3

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics