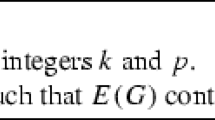Abstract
We consider the problem of finding a local optimum for the Max-Cut problem with FLIP-neighborhood, in which exactly one node changes the partition. Schäffer and Yannakakis (SICOMP, 1991) showed \(\mathcal{PLS}\)-completeness of this problem on graphs with unbounded degree. On the other side, Poljak (SICOMP, 1995) showed that in cubic graphs every FLIP local search takes O(n 2) steps, where n is the number of nodes. Due to the huge gap between degree three and unbounded degree, Ackermann, Röglin, and Vöcking (JACM, 2008) asked for the smallest d such that on graphs with maximum degree d the local Max-Cut problem with FLIP-neighborhood is \(\mathcal{PLS}\)-complete. In this paper, we prove that the computation of a local optimum on graphs with maximum degree five is \(\mathcal{PLS}\)-complete. Thus, we solve the problem posed by Ackermann et al. almost completely by showing that d is either four or five (unless \(\mathcal{PLS}\) ⊆ \(\mathcal{P}\)).
On the other side, we also prove that on graphs with degree O(logn) every FLIP local search has probably polynomial smoothed complexity. Roughly speaking, for any instance, in which the edge weights are perturbated by a (Gaussian) random noise with variance σ 2, every FLIP local search terminates in time polynomial in n and σ − 1, with probability 1 − n − Ω(1). Putting both results together, we may conclude that although local Max-Cut is likely to be hard on graphs with bounded degree, it can be solved in polynomial time for slightly perturbated instances with high probability.
Partially supported by the German Research Foundation (DFG) Priority Programme 1307 “Algorithm Engineering”.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Arthur, D., Manthey, B., Röglin, H.: k-Means has polynomial smoothed complexity. In: FOCS 2009, pp. 405–414 (2009)
Ackermann, H., Röglin, H., Vöcking, B.: On the impact of combinatorial structure on congestion games. Journal of the ACM (JACM) 55(6), art. 25 (2008)
Blum, A., Dunagan, J.: Smoothed analysis of the perceptron algorithm for linear programming. In: SODA, pp. 905–914 (2002)
Beier, R., Vöcking, B.: Typical properties of winners and losers in discrete optimization. In: STOC, pp. 343–352 (2004)
Englert, M., Röglin, H., Vöcking, B.: Worst case and probabilistic analysis of the 2-Opt algorithm for the TSP. In: SODA, pp. 1295–1304 (2006)
Fabrikant, A., Papadimitriou, C.H., Talwar, K.: The complexity of pure Nash Equilibria. In: STOC, pp. 604–612 (2004)
Gairing, M., Savani, R.: Computing stable outcomes in hedonic games. In: Kontogiannis, S., Koutsoupias, E., Spirakis, P.G. (eds.) Algorithmic Game Theory. LNCS, vol. 6386, pp. 174–185. Springer, Heidelberg (2010)
Garey, M.R., Johnson, D.S.: Computers and intractability, a guide to the theory of NP-completeness. Freeman, New York (1979)
Johnson, D.S., Papadimitriou, C.H., Yannakakis, M.: How easy is local search? Journal of Computer and System Sciences 37(1), 79–100 (1988)
Krentel, M.W.: Structure in locally optimal solutions. In: FOCS, pp. 216–221 (1989)
Kelner, J.A., Nikolova, E.: On the hardness and smoothed complexity of quasi-concave minimization. In: FOCS, pp. 472–482 (2007)
Loebl, M.: Efficient maximal cubic graph cuts. In: Leach Albert, J., Monien, B., Rodríguez-Artalejo, M. (eds.) ICALP 1991. LNCS, vol. 510, pp. 351–362. Springer, Heidelberg (1991)
Monien, B., Dumrauf, D., Tscheuschner, T.: Local search: Simple, successful, but sometimes sluggish. In: Abramsky, S., Gavoille, C., Kirchner, C., Meyer auf der Heide, F., Spirakis, P.G. (eds.) ICALP 2010. LNCS, vol. 6198, pp. 1–17. Springer, Heidelberg (2010)
Monien, B., Tscheuschner, T.: On the power of nodes of degree four in the local max-cut problem. In: Calamoneri, T., Diaz, J. (eds.) CIAC 2010. LNCS, vol. 6078, pp. 264–275. Springer, Heidelberg (2010)
Poljak, S.: Integer linear programs and local search for max-cut. SIAM Journal on Computing 21(3), 450–465 (1995)
Poljak, S., Tuza, Z.: Maximum cuts and largest bipartite subgraphs. Combinatorial Optimization, pp. 181–244. American Mathematical Society, Providence (1995)
Röglin, H.: Personal communication (2010)
Röglin, H., Vöcking, B.: Smoothed analysis of integer programming. Math. Program. 110(1), 21–56 (2007)
Spielmann, D., Teng, S.-H.: Smoothed analysis of algorithms: Why the simplex algorithm usually takes polynomial time. Journal of the ACM (JACM) 51(3), 385–463 (2004)
Spielmann, D., Teng, S.-H.: Smoothed analysis: an attempt to explain the behavior of algorithms in practice. Commun. ACM 52(10), 76–84 (2009)
Schäffer, A.A., Yannakakis, M.: Simple local search problems that are hard to solve. SIAM Journal on Computing 20(1), 56–87 (1991)
Vershynin, R.: Beyond Hirsch Conjecture: Walks on Random Polytopes and Smoothed Complexity of the Simplex Method. In: FOCS, pp. 133–142 (2006)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Elsässer, R., Tscheuschner, T. (2011). Settling the Complexity of Local Max-Cut (Almost) Completely. In: Aceto, L., Henzinger, M., Sgall, J. (eds) Automata, Languages and Programming. ICALP 2011. Lecture Notes in Computer Science, vol 6755. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-22006-7_15
Download citation
DOI: https://doi.org/10.1007/978-3-642-22006-7_15
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-22005-0
Online ISBN: 978-3-642-22006-7
eBook Packages: Computer ScienceComputer Science (R0)