Abstract
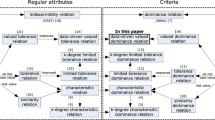
In this paper, we present an explorative research focusing on dominance–based rough set approach to the incomplete information systems. In most of the rough set literatures, an incomplete information system indicates an information system with unknown values. By assuming that the unknown value can be compared with any other values in the domain of the corresponding attributes, the concept of the valued dominance relation is proposed to show the probability that an object is dominating another one. The fuzzy rough approximations in terms of the valued dominance relation are then constructed. It is shown that by the valued dominance–based fuzzy rough set, we can obtain greater lower approximations and smaller upper approximations than the old dominance–based rough set in the incomplete information systems. Further on the problem of inducing “at least” and “at most” decision rules from incomplete decision system is also addressed. Some numerical examples are employed to substantiate the conceptual arguments.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Pawlak, Z.: Rough sets–theoretical aspects of reasoning about data. Kluwer Academic Publishers, Dordrecht (1991)
Pawlak, Z.: Rough set theory and its applications to data analysis. Cybernet. Syst. 29, 661–688 (1998)
Pawlak, Z.: Rough sets and intelligent data analysis. Inform. Sci. 147, 1–12 (2002)
Pawlak, Z., Skowron, A.: Rudiments of rough sets. Inform. Sci. 177, 3–27 (2007)
Pawlak, Z., Skowron, A.: Rough sets: some extensions. Inform. Sci. 177, 28–40 (2007)
Pawlak, Z., Skowron, A.: Rough sets and boolean reasoning. Inform. Sci. 177, 41–73 (2007)
Greco, S., Matarazzo, B., Słowiński, R.: Rough approximation by dominance relations. Int. J. Intell. Syst. 17, 153–171 (2002)
Greco, S., Matarazzo, B., Słowiński, R.: Rough sets theory for multicriteria decision analysis. Eur. J. Oper. Res. 129, 1–47 (2002)
Greco, S., Inuiguchi, M., Słowiński, R.: Fuzzy rough sets and multiple–premise gradual decision rules. Int. J. Approx. Reason. 41, 179–211 (2006)
Błaszczyński, J., Greco, S., Słowiński, R.: Multi–criteria classification–A new scheme for application of dominance–based decision rules. Eur. J. Oper. Res. 181, 1030–1044 (2007)
Fan, T.F., Liu, D.R., Tzeng, G.H.: Rough set–based logics for multicriteria decision analysis. Eur. J. Oper. Res. 182, 340–355 (2007)
Kryszkiewicz, M.: Rough set approach to incomplete information systems. Inform. Sci. 112, 39–49 (1998)
Latkowski, R.: Flexible indiscernibility relations for missing attribute values. Fund. Inform. 67, 131–147 (2005)
Leung, Y., Li, D.Y.: Maximal consistent block technique for rule acquisition in incomplete information systems. Inform. Sci. 115, 85–106 (2003)
Leung, Y., Wu, W.Z., Zhang, W.X.: Knowledge acquisition in incomplete information systems: a rough set approach. Eur. J. Oper. Res. 168, 464–473 (2006)
Wang, G.Y.: Extension of rough set under incomplete information systems. In: Proceeding of the 11th IEEE International Conference on Fuzzy Systems, pp. 1098–1103 (2002)
Grzymala–Busse, J.W.: Characteristic relations for incomplete data: a generalization of the indiscernibility relation. In: Proceeding of the Third International Conference on Rough Sets and Current Trends in Computing, pp. 244–253 (2004)
Grzymała-Busse, J.W.: Data with missing attribute values: Generalization of indiscernibility relation and rule induction. In: Peters, J.F., Skowron, A., Grzymała-Busse, J.W., Kostek, B.z., Świniarski, R.W., Szczuka, M.S. (eds.) Transactions on Rough Sets I. LNCS, vol. 3100, pp. 78–95. Springer, Heidelberg (2004)
Wu, W.Z., Zhang, W.X., Li, H.Z.: Knowledge acquisition in incomplete fuzzy information systems via the rough set approach. Expert Syst. 20, 280–286 (2003)
Yang, X.B., Yang, J.Y., Wu, C., Yu, D.J.: Dominance–based rough set approach and knowledge reductions in incomplete ordered information system. Inform. Sci. 178, 1219–1234 (2007)
Shao, M.W., Zhang, W.X.: Dominance relation and rules in an incomplete ordered information system. Int. J. Intell. Syst. 20, 13–27 (2005)
Stefanowski, J., Tsoukiàs, A.: Incomplete information tables and rough classification. Comput. Intell. 17, 545–566 (2001)
Stefanowski, J., Tsoukiàs, A.: On the extension of rough sets under incomplete information. In: Proceeding of New Directions in Rough Sets, Data Mining and Granular–Soft Computing, pp. 73–82 (1999)
Dubois, D., Prade, H.: Rough fuzzy sets and fuzzy rough sets. Int. J. Gen. Syst. 17, 191–208 (1990)
Yeung, D.S., Chen, D.G., Tsang, E.C.C., Lee, J.W.T., Wang, X.Z.: On the generalization of fuzzy rough sets. IEEE T. Fuzzy Syst. 13, 343–361 (2005)
Morsi, N.N., Yakout, M.M.: Axiomatics for fuzzy rough sets. Fuzzy Set. Syst. 100, 327–342 (1998)
Bhatt, R.B., Gopal, M.: On the compact computational domain of fuzzy-rough sets. Pattern Recogn. Lett. 26, 1632–1640 (2005)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Yang, X., Dou, H. (2011). Valued Dominance-Based Rough Set Approach to Incomplete Information System. In: Gavrilova, M.L., Tan, C.J.K. (eds) Transactions on Computational Science XIII. Lecture Notes in Computer Science, vol 6750. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-22619-9_5
Download citation
DOI: https://doi.org/10.1007/978-3-642-22619-9_5
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-22618-2
Online ISBN: 978-3-642-22619-9
eBook Packages: Computer ScienceComputer Science (R0)