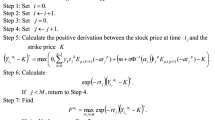Skip to main content
Springer Nature Link
Log in

Pricing Formulas of Compound Options under the Fractional Brownian Motion

  • Conference paper
Nonlinear Mathematics for Uncertainty and its Applications

Part of the book series: Advances in Intelligent and Soft Computing ((AINSC,volume 100))

  • 1951 Accesses

Abstract

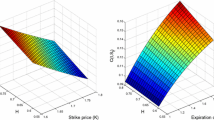
In this paper, the pricing formulas of the compound options under the fractional Brownian motion are given by the method of partial differential equation.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Bender, C., Sottinen, T., Valkeila, E.: Arbitrage with fractional Brownian Motion. Theory of Stochastics Process 12, 3–4 (2006)

    Google Scholar 

  2. Cheridito, P.: Arbitrage in fractional Brownian Motion models. Finance and Stochastics 7, 533–553 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  3. Fischer, B., Myron, S.: The pricing of option and corporate liabilities. J. Political Economy 81, 637–654 (1973)

    Article  Google Scholar 

  4. Guasoni, P.: No arbitrage under transaction costs with fractional Brownian motion and beyond. Mathematical Finance 16, 569–582 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  5. Hu, Y.Z., Oksendal, B.: Fractional white noise calculus and application to finance. infinite dimensional analysis. Quantum Probability and Related Topics 6, 1–32 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  6. Jiang, L.S.: Mathematical Modeling and Methods of Option Pricing. World Scientific Publishing Company, Singapore (2005)

    MATH  Google Scholar 

  7. Kolmogorov, A.: Wienersche Spiralen und einige andere interessante Kurven in Hilbertschen Raum. Comptes Rendus (Doklady) de l’Academie des Sciences de l’URSS 26, 115-118 (1940)

    Google Scholar 

  8. Louis, B.: Theorie de la speculation. Annales Scientifiques de l’Ecole Normale Superieure 17, 21–86 (1900)

    MathSciNet  Google Scholar 

  9. Mandelbrot, B.B., Van Ness, J.W.: Fractional Brownian motions.Fractional Noises and Applications. Siam Review 10, 422–437 (1968)

    Article  MathSciNet  MATH  Google Scholar 

  10. Merton, R.C.: Theory of rational option pricing, Bell. J. Econ. & Manag. Sci. 4, 141–183 (1973)

    MathSciNet  Google Scholar 

  11. Necula, C.: Option pricing in a fractional Brownian Motion environment. Draft. Academy of Economic Studies 12, 1–18 (2002)

    Google Scholar 

  12. Nualart, D.: Stochastic Integration with Respect to Fractional Brownian Motion and Applications (2004) (preprint)

    Google Scholar 

  13. Nualart, D., Rascanu, A.: Differential equations driven by fractional Brownian Motion. Collectanea Mathematica 53(1), 55–81 (2002)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Shanghai Normal University, Shanghai, 200234, China

    Chao Zhang & Jizhou Zhang

  2. School of Mathematical Sciences, Xuzhou Normal University, China

    Dongya Tao

Authors
  1. Chao Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jizhou Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dongya Tao
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. College of Applied Sciences, Beijing University of Technology, 100 Pingleyuan, 100124, Chaoyang District, Beijing, P.R. China

    Shoumei Li , Xia Wang  & Li Guan ,  & 

  2. Department of Systems Design and Informatics, Kyushu Institute of Technology, 680-4, Kawazu, 820-8502, lizuka, Japan

    Yoshiaki Okazaki

  3. Department of Mathematics, Shinshu University, 4-17-1 Wakasato, 380-8553, Nagano, Japan

    Jun Kawabe

  4. Department of Computational Intelligence and Systems Science, Tokyo Institute of Technology, 4259-G3-47, Nagatsuta, Midori-ku, 226-8502, Yokohama, Japan

    Toshiaki Murofushi

Rights and permissions

Reprints and permissions

Copyright information

© 2011 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Zhang, C., Zhang, J., Tao, D. (2011). Pricing Formulas of Compound Options under the Fractional Brownian Motion. In: Li, S., Wang, X., Okazaki, Y., Kawabe, J., Murofushi, T., Guan, L. (eds) Nonlinear Mathematics for Uncertainty and its Applications. Advances in Intelligent and Soft Computing, vol 100. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-22833-9_29

Download citation

  • DOI: https://doi.org/10.1007/978-3-642-22833-9_29

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-642-22832-2

  • Online ISBN: 978-3-642-22833-9

  • eBook Packages: EngineeringEngineering (R0)

Publish with us

Policies and ethics